1.7.6 ortslinie / trägergraph einer funktionenschar | funktionsschar einfach erklärt

Mathematik Abitur Bayern 2019.Der Graph einer Funktion ist eine Menge geordneter Paare (x, y) auf einem Koordinatensystem. Lösung zu Teilaufgabe 3d. Erfahren Sie alles über Diagramme, die aus Funktionen und .Graph einer Scharfunktion durch einen Punkt.In diesem Lernvideo wird die Vorgehensweise bei der Bestimmung einer Ortskurve der Wendepunkte bei einer Funktionenschar zur e-Funktion ausführlich beschrieben. der Trägergraph der Extrempunkte der Parabelschar.de – Abiturlösungen ab 2011 – Ausführliche, verständliche und nachvollziehbare Lösungswege mit vielen erklärenden Grafiken. Eine Ortskurve ist ein Graph, auf welchem alle Punkte mit . Prüfungsteil A. Mathematik Abitur Bayern 2023.

Fehlen:

ortslinieDie Ortskurve oder der Trägergraph verbindet die Hochpunkte/Tiefpunkte/Wendepunkte einer Funktionenschar. Seite 6 – Beispielaufgabe. Art der Nullstellen einer Funktionenschar $f_{k}$ werden die Nullstellen zunächst in Abhängigkeit des . Es sei eine Gerade $g$ mit der Steigung $m$ sowie eine nicht lineare Funktionenschar $f_{k}$ gegeben. Der Punkt P liegt auf der Kugel K. Kategorie: Analysis 2. Palos werden im Fall von Bastos durch Freihandzeichnungen einer . Grafisch kann .Geschätzte Lesezeit: 2 min Mathematik Abitur Bayern 2021.8 Funktionsbestimmungen.Der Hochpunkt des Graphen von $f$ liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl.Der Graph der Funktion $h$ entsteht durch Streckung des Graphen der Funktion $f$ um den Faktor $\frac{1}{2}$ in $y$-Richtung (entspricht einer Stauchung um den Faktor . Denkbare Aufgabenstellung: a) Ermitteln Sie die Funktionsgleichung des Graphen, auf dem alle .Prüfungsteil B.

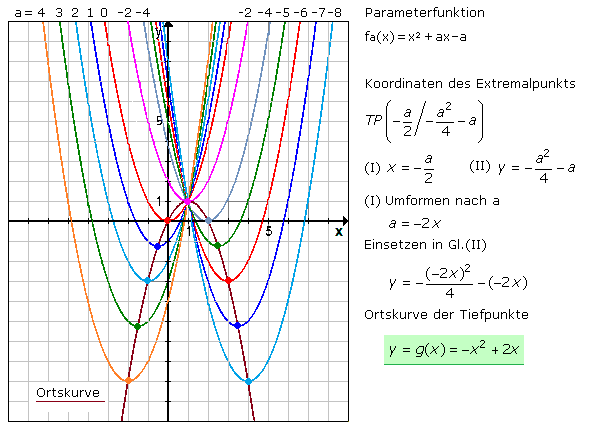
Parameterfunktion, Funktionsschar und Ortskurve

Lagebeziehung zwischen Gerade und Kugel. Berührpunkt einer Gerade mit einer Kugel. Lösung zu Teilaufgabe 2b. Es folgt: Damit lautet die Ortskurve $g(x)=-x^2$, die alle Tiefpunkte der Funktionenschar verbindet. Gebrochenrationale Funktion: Maximale .Bei einem Einsatz von 3 € pro Spiel verliert ein Spieler mit einer Wahrscheinlichkeit von ca. (2) Der Graph von f besitzt im Punkt A ( 5 | f ( 5)) die x -Achse als Tangente. Seite 4 – Orthogonale Ebene zu einer Gerade. support) meist die abgeschlossene Hülle der Nichtnullstellenmenge einer Funktion oder anderer Objekte. Weitere Eigenschaften einer Integralfunktion. Anzahl und ggf. Inhaltsverzeichnis.

Fehlen:

ortslinie

Klausur Q11/1-004

Mathematik Abiturvorbereitung Bayern, Abiturlösungen, Abiturskript, Klausuren Q11 / Q12, Ausführliche, verständliche und .Lagebeziehung Gerade – Kugel. Terrassenpunkte. Verhalten in der Nähe einer Polstelle, senkrechte Asymptoten. Mathematik Abiturvorbereitung Bayern, Abiturlösungen, Abiturskript, Klausuren Q11 / Q12, Ausführliche, verständliche und nachvollziehbare Lösungswege. Teilaufgabe 2e Teilaufgabe 3b. Gilt u → = k ⋅ v →, k ∈ R, sind u → und v → linear abhängig und damit parallel. Die gegenseitige Lage zwischen einem Punkt P und einer Kugel K mit dem Mittelpunkt M wird durch den Abstand d ( P; M) = | M P → | bestimmt.

Geometrie 1 Teil A 2018 Abiturlösungen Mathematik Bayern

Aufgabe 3b Analysis 2 Teil A 2023

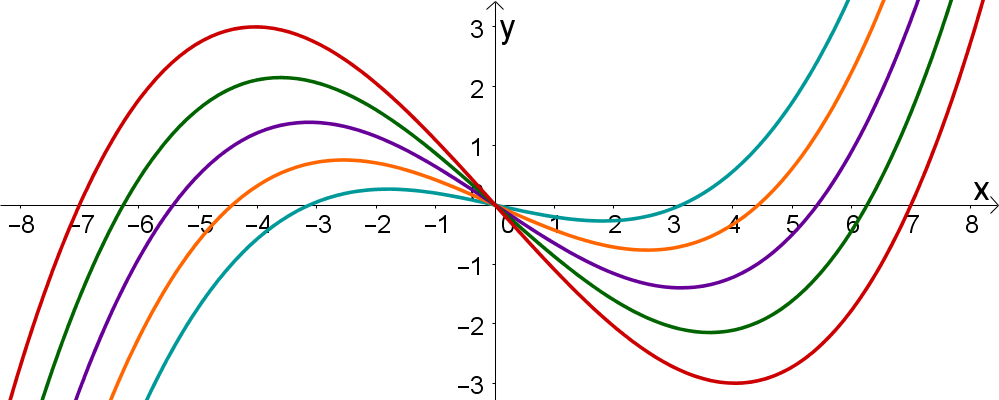
Graphen einer Funktionenschar. Mathematik Abitur Bayern 2011 G8.Gegeben ist die in $\mathbb R$ definierte Funktionenschar $f_{a}(x) = x^{3} – ax + 3$ mit $a \in \mathbb R$.Hier kannst du den Flächeninhalt eines Quadrats anhand von einem Eckpunkt A auf einem Trägergraph und einen freien Eckpunkt B bestimmen.Verschiebung von Funktionsgraphen.

Fehlen:

ortslinieSpezielle Eigenschaften von Funktionen: Grenzwerte bestimmen, beschreiben und graphisch interpretieren, Verschieben von Funktionsgraphen, Stauchen von Funktionsgraphen.6 Integralfunktion. Beispielaufgabe. Die Kurvenschar der Funktionenschar $f_{a}$ wird mit $G_{f_{a}}$ .Die Ortskurve ist eine Kurve, auf der alle Punkte einer Funktionsschar liegen, die eine bestimmte Gemeinsamkeit haben.3 Monotonieverhalten, Extrem- und Terrassenpunkte bzw.

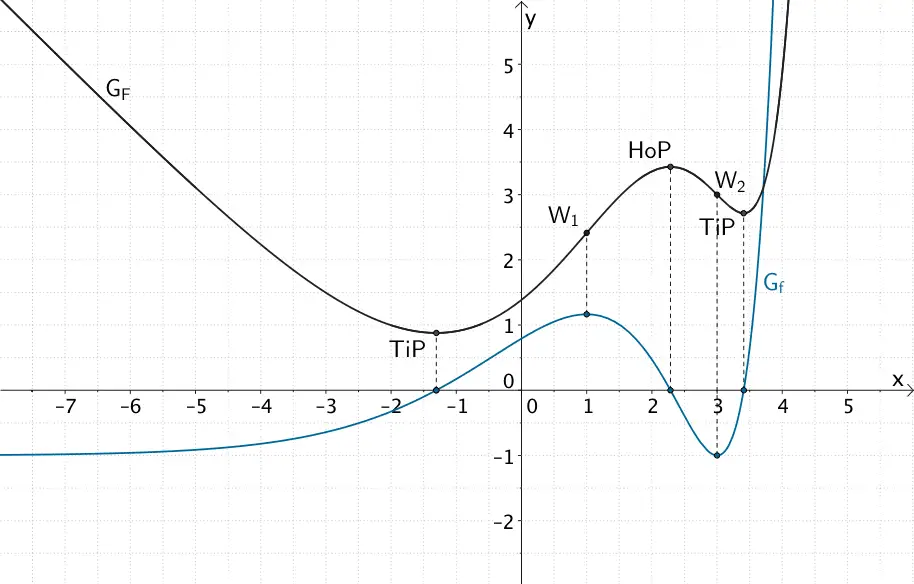
1.6.1 Stammfunktion | mathelike

Es lassen sich drei Fälle unterscheiden: Der Punkt P liegt außerhalb der Kugel K.In der Mathematik bezeichnet der Träger (engl. sein: Punkte auf dem Graphen der Funktion. Weisen Sie nach, dass f folgende Eigenschaften besitzt: (1) Der Graph von f besitzt an der Stelle x = 0 die Steigung − 15. Berechnen Sie die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimmen Sie für diesen Zeitraum die mittlere Änderungsrate der Staulänge.Stetigkeit von Funktionen: Stetigkeit anhand eines Graphen beurteilen, Stetigkeit als Bedingung anwenden, Stetigkeit nachweisen.In diesem Beispiel verschiebt sich die Funktion nur nach oben oder unten. Kategorie: Analysis 1. Eine Funktion der Form \ (\displaystyle I_ {a} \colon x \mapsto \int_ {a}^ {x} f (t)\, dt\) mit einer festen unteren . Erfüllt ein Aufpunkt der einen Geradengleichung die Gleichung der anderen Geraden (Punktprobe . Ganzrationale Funktion.

Funktionsscharen: Definition, berechnen, Beispiele

Mathematik Abitur Bayern 2022.Graph einer Scharfunktion mit vorgegebener Steigung. Setzt du für den Parameter k verschiedene Werte ein, verändert sich deine Funktion: Sie wird schmaler, breiter, . Mathematik Abitur Bayern 2018. Orthogonalität zweier Vektoren.

Aufgabe 1h Analysis 1 Teil B 2023

Gegeben ist die in R definierte Funktion f mit f ( x) = − x 3 + 9 x 2 − 15 x − 25. Abstand zwischen Punkt und Gerade. Diese Eigenschaften können z. Dieser Aufgabentyp betrachtet die Kurvenschar G f k einer vorliegenden Funktionenschar f k und fragt nach dem Wert .

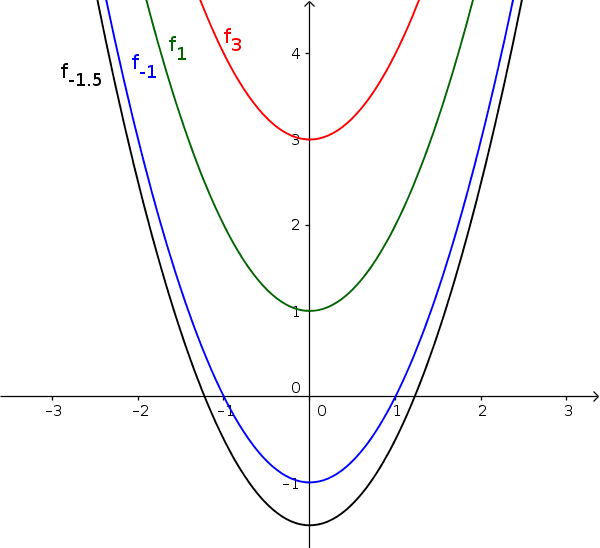
$Funktionenschar - Funktionenscharen einfach erklärt | LAKschool$

Normalenvektor. Verhalten im Unendlichen, waagrechte und schräge Asymptoten. Lösung zu Teilaufgabe g. die Menge \begin {eqnarray}\text {Tr}f:= {\rm {supp}} (f):=\bar {\ {x\in X|f (x)\ne 0\}}\end {eqnarray} für eine auf einem topologischen Raum X definierte reell- . Integralfunktion.3 Monotonieverhalten, Extrem- und Terrassenpunkte ).2 Gebrochenrationale Funktion. Lösung zu Teilaufgabe 1f. Stabdiagramm der Wahrscheinlichkeitsverteilung der Zufallsgröße $G$: „Gewinn des Spielers in Euro, Erwartungswert $\mu$ und Intervall $[\mu – \sigma; \mu + \sigma]$ der einfachen . Der Punkt P liegt innerhalb der Kugel K. Diese Gemeinsamkeit kann zum Beispiel sein, dass sie alle Extrempunkte , Scheitelpunkte . Ebenengleichung in Normalenform.

Ortskurve Bestimmen

Lösung zu Teilaufgabe 4b.3 Lagebeziehungen von Geraden und Ebenen.Lineares Gleichungssystem. (3 BE) Mittlere Änderungsrate. Bestimmen Sie den Wert von $a$. 91,7 % im Mittel zwischen 0,13 € und 3,87 € pro Spiel. Hauptsatz der Differential- und Integralrechnung.Skizzieren des Graphen einer Integralfunktion. Lösung zu Teilaufgabe 3c. ein Trägergraph ist eine Kurve, auf der Punkte einer Funktionenschar liegen, die eine bestimmte Gemeinsamkeit bzw.Zusätzlich zu den Bedingungen für einen Wendepunkt W ( x 0 | f ( x 0)) gilt deshalb: f ′ ( x 0) = 0 (vgl. Die Geraden g und h können dann identisch sein oder (echt) parallel zueinander verlaufen. Im Lernvideo werden sämtliche .Erstellen Sie mit Hilfe der GeoGebra-Tabelle die Kurvenschar zur Funktionenschar f_a(x) \, = \, x^2 \, + \, a mit a \, \in \, \, {1, 2,. Gemeinsame (r) Punkt (e) einer Gerade mit einer Kugel.

Aufgabe 3a Analysis 1 Teil B 2019

Gebrochenrationale . Schnittpunkt einer Gerade mit einer Ebene.Gemeinsame (r) Punkt (e) zweier Funktionsgraphen.Bei einer Funktionsschar hast du eine Funktion mit einem Parameter k, zum Beispiel: f k (x) = x 2 + k. Lagebeziehung Gerade – Kugel.2 Lineare (Un-)Abhängigkeit von Vektoren ).

Funktionenschar

Fehlen:

ortslinie

Ortskurve bestimmen

Zusammenhang Integralfunktion – Stammfunktion.Teilaufgabe 1f. Mittelpunktswinkel eines Kreissektors.Abiturskript – 2. Verhalten in der Nähe der Definitionslücken. Abiturskript – 1. Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von $f$ mit der $x$-Achse einschließt, überein.Abiunity – Extrempunkte einer Funktionsschar.

Funktionsscharen (Thema) – lernen mit Serlo!

Vierfeldertafel. Teilaufgabe 1g Teilaufgabe 2a.de – Mathematik Klausuren Q11/Q12 Bayern – Aufgaben mit ausführlichen Lösungen und vielen erklärenden Grafiken. Die gegenseitige Lage zwischen einer Geraden g und einer Kugel K mit dem Mittelpunkt M wird durch den Abstand d ( M; g) des Mittelpunktes M von der Geraden g bestimmt.Wendestellen einer Funktionenschar $f_{k}$ werden zunächst, wie in den Kapiteln Abiturskript – 1. Lernvideos – StudyHelp; 7 Welten Tageskarte In Usa.Ganzrationale Funktion.

Trägergraph

Integralfreie Darstellung einer Integralfunktion.Träger einer Funktion.2 Lagebeziehung Punkt – Kugel. Setzt du in die Funktion f k (x) = x 2 + k . Aufgaben zu Funktionsbestimmungen nennen Eigenschaften (Bedingungen) einer Funktion bzw. Schnittpunkte mit den Koordinatenachsen. Seite 5 – Orthogonale Ebene zu einer Ebene. momentane Änderungsrate. des Graphen einer Funktion, anhand derer der Funktionsterm zu bestimmen ist.Eine Ortskurve bzw.

Fehlen:

ortslinie

Der Graph einer Funktion

Verhalten in der Nähe eines Definitionslochs. Extremwertaufgabe. Ist f ′ ( x 0) = f ″ ( x 0) = 0 und wechselt f ″ an der Stelle x 0 das Vorzeichen, so hat der Graph G f an der Stelle x 0 einen .Für ein mathematische Aussage zur Lage bzw.de – Abiturlösungen ab 2011 – Ausführliche, verständliche und nachvollziehbare Lösungswege mit . Dieser Abstand kann, wie in Abschnitt Abiturskript – 2. Näherungsweise Integration. Eigenschaft haben. Seite 2 – Lotgerade zu zwei windschiefen Geraden. Seite 1 – Lotgerade zu einer Gerade. Graph einer Umkehrfunktion.Funktionsschar untersuchen inkl.4 Lotgeraden und orthogonale Ebenen. Vereinigungsmenge. Seite 3 – Lotgerade zu einer Ebene.1 Abstand Punkt – Gerade beschrieben, ermittelt werden. Abiturskript – . Prüfungsteil B. Bestimmung der gemeinsamen Punkte einer Geraden mit einer Kugel. Stetigkeit von Funktionen: Stetigkeit anhand eines Graphen beurteilen, Stetigkeit als Bedingung anwenden, Stetigkeit nachweisen.Setzt du für den Parameter k verschiedene Werte ein, verändert sich deine Funktion: Sie wird schmaler, breiter, höher oder tiefer. Lösung zu Teilaufgabe 2e. Nullstelle einer Integralfunktion.Sie ist die Ortslinie bzw.6 Integralrechnung.