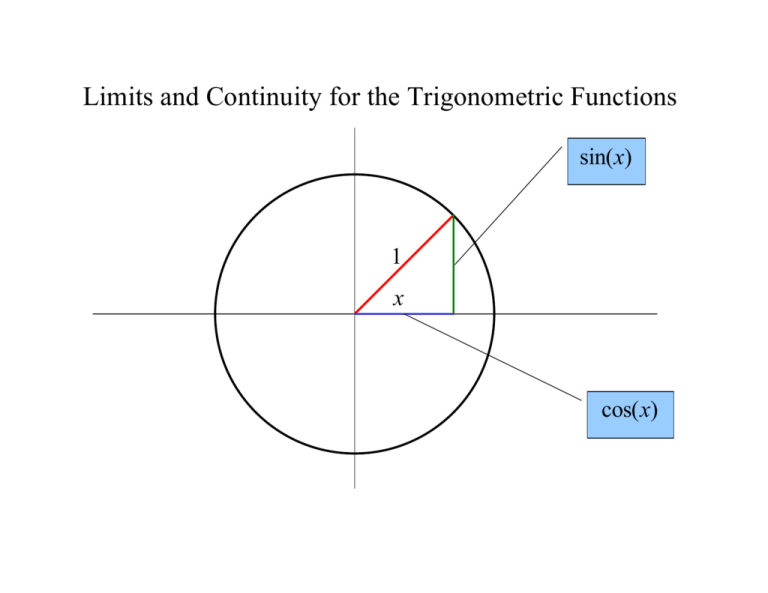
Then we apply these .The graph of a function is the set of all these points. For the following exercises, find the values for each function, if they exist, then simplify.4: Here we see a graph of the function f with domain 1, 2, 3 and rule f(x) = 3 − x. Let Δy = y2 − y1 and Δx = x2 − x1 denote the changes in y and x, respectively. Figure illustrates this idea. The slope of the line is.4 Estimating Limit .5 includes piecewise functions involving limits) 1.4, we plot a graph of this function. limx→0 ln x lim x → 0 ln x.Unit 1 – Limits and Continuity 1. In many cases, an algebraic approach may .1 Answers
FUNCTIONS OF SEVERAL VARIABLES 1 Limits and Continuity
How are the characteristics of a function having a limit, being continuous, and being differentiable at a given point related to one another? In Section 1.This theorem allows us to calculate limits by “squeezing” a function, with a limit at a point a that is unknown, between two functions having a common known limit at a. Recall that the de ̄nition of the limit of such .The geometric approach to proving that the limit of a function takes on a specific value works quite well for some functions.

Schlagwörter:Squeeze TheoremTheorems and LemmasProof of Trig Limits

Solution manuals are also available.1 Interpreting the Meaning of the Derivative in Context 4., state why the formal . In this section we learn the definition of continuity and we study the types of discontinuities.Schlagwörter:Exponential and Logarithmic FunctionsExponential To Logarithmic5 Selecting Procedures for Calculating Derivatives 3.The function \(f(x)=2^x−x^3\) is continuous over the interval [\(1.Schlagwörter:CalculusContinuity of A Limit1 Can Change Occur at an Instant? .1 Given a function f, the limit of f (x) as x approaches c is a real number R if f (x) can be made arbitrarily close to R by taking x sufficiently close to c (but not equal to c).

Schlagwörter:Derivatives of Inverse FunctionsInverse Trig Functions7: Limit of Trigonometric functions; 1.4 Differentiating Inverse Trigonometric Functions 3. Before we look at a formal definition of what it means for a function to be continuous at a point, let’s consider various functions . For the following exercises, (a) determine the domain and the range of each relation, and (b) state whether the relation is a function. \ ( \newcommand {\vecs} [1] {\overset { \scriptstyle \rightharpoonup} {\mathbf {#1}} } \) \ ( \newcommand {\vecd} [1] {\overset {-\! . Also, the insight into the formal definition of the limit that this method provides is invaluable.The two fundamental specific limits results which follow easily from the definition are: (1) If c ∈ R, then lim c = c and (2) lim x = x→a.A table of values or graph may be used to estimate a limit. Proof of : lim θ→0 sinθ θ = 1 lim θ → 0.1 Can Change Occur at an Instant? 1. We are now going to consider the problem of finding the derivatives of the . File Size: 446 kb.6 Calculating Higher-Order Derivatives Review – Unit 3.6 Determining Limits Using Algebraic . Exercise \(\PageIndex{6}\) 1) Consider the graph of the function \(y=f(x)\) shown in the following graph.

A function is continuous on an interval if we can draw the graph from start to finish without ever once picking up our pencil.Schlagwörter:Inverse Trigonometric FunctionsCalculuschrome_reader_mode Enter Reader Mode . Hint : Remember the process described in this section. We can use the inverse . Explain the relationship .chrome_reader_mode Insert Reader Mode . The inverse sine function is sometimes called the arcsine function, and notated arcsinx.Use the formulas listed in the rule on integration formulas resulting in inverse trigonometric functions to match up the correct format and make alterations as . The inverse sine function y = sin − 1x.1 Limits and Continuity.

Verify your inverse by computing one or both of the composition as discussed in this section. In order to derive the derivatives of inverse trig functions we’ll need the . We analyze the behaviour of f(x) f ( x) around x = −5, x = − 5, x = −2, x = − 2, x= −1 x = − 1 and x = 0, x = . Formulas for the remaining three could be derived by a similar process as we did those above.In this section we’re going to provide the proof of the two limits that are used in the derivation of the derivative of sine and cosine in the Derivatives of Trig Functions section of the Derivatives chapter. The graph in the last example has only two discontinuities since there are .The tangent lines of a function and its inverse are related; so, too, are the derivatives of these functions. For the following exercises, find the domain . If the limit exists and is a real number, then.In aforementioned teilbereich we will introduce and concept of continuity both how it pertains to limits.3 Limits Graphically. For each value in part a. For example, consider the function f, where the domain is the set D = 1, 2, 3 and the rule is f(x) = 3 − x. means x = sin y. Define one-sided limits and provide examples. This page is a draft and is under active development.chrome_reader_mode Register Reader Run . Then by differentiating both sides of this equation (using the chain rule on the right), we obtain. The course below follows CollegeBoard’s Course and Exam Description.The derivative of the inverse tangent is then, d dx (tan−1x) = 1 1 +x2 d d x ( tan − 1 x) = 1 1 + x 2. Find the limits as \(x→∞\) and \(x→−∞\) for \(f(x)=\frac{(2+3e^x)}{(7−5ex^)}\) .This page is a draft and is under active development. We may also derive the formula for the derivative of the inverse by first recalling that . We begin with a review of the concepts of limits and continuity for real-valued functions of one variable.On these restricted domains, we can define the inverse trigonometric functions.Schlagwörter:CalculusMatthew Boelkins1: Limit and Continuity of Functions.chrome_reader_mode Enter Reader Manner .Example \(\PageIndex{8}\): Determining End Behavior for a Transcendental Function. Intuitively, a function is continuous at a particular point if there is no break in its graph at that point. In this section we’re going to provide the proof of the two limits that are used in the derivation of the derivative of sine and cosine in the Derivatives of Trig Functions section of the Derivatives chapter. y = sin − 1x has domain [−1, 1] and range [− π 2, π 2]
Unit 1
3 : Proof of Trig Limits. y = sin − 1 x. We will other see aforementioned Intermediate Value Theorem include this section and how it can be used to determine if .5 Determining Limits Using Algebraic Properties (1. However, we may also approach limit proofs from a purely algebraic point of view. a for any a ∈ R.
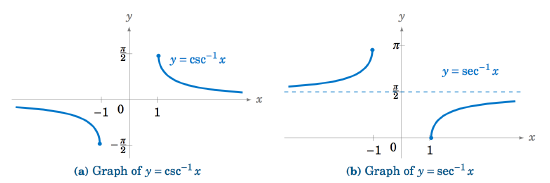
Let us start by playing with the sine function and determine how to restrict the domain of \(\sin x\) so that its inverse function exists.In this chapter we introduce the concept of limits. Limits can be used to give precise meaning to the concept of . m = y2 − y1 x2 − x1 = Δy Δx.2 Defining Limits and Using Limit Notation 1. Unit 4 – Contextual Applications of Differentiation 4. The graph of a function f(x) f ( x) is shown below.2, we learned how limits can be used to study . We will discuss the interpretation/meaning of a limit, how to evaluate limits, the definition and evaluation of . One very useful application of implicit differentiation is to find the derivatives of inverse functions. We have already used this approach to find the derivative of the inverse of the exponential function — the logarithm.3: Limit calculations for algebraic expressions Expand/collapse global locationWe examine how to find an inverse function and study the relationship between the graph of a function and the graph of its inverse.Expand/collapse global hierarchy Home Campus Bookshelves Mount Royal University2 Straight-Line . Inverse Trigonometric Functions.8: Limits and continuity of Inverse Trigonometric functionsSchlagwörter:Inverse Trigonometric FunctionsLimits and Continuity of Functions Want to save money on printing? Support us and buy the Calculus workbook with all the packets in one nice spiral bound book. It was built for a 45-minute class period that meets every day, so the lessons are shorter than .3) We now examine the relationship between slope and the formula for a linear function. Find all values for which the function is discontinuous.Schlagwörter:Limits and Continuity of FunctionsContinuity of A Limitchrome_reader_mode Record Reader Mode . The inverse function theorem allows us to compute derivatives of inverse functions without using the limit definition of the derivative.375\)] and has opposite signs at the endpoints.Schlagwörter:Limits and Continuity of FunctionsContinuity of A Limit
Unit 1
We begin our investigation of continuity by exploring what it means for a function to have continuity at a point. If the limit of a function at a point does not exist, it is still possible that the limits from the left and right at that point may exist.Schlagwörter:Limits and Continuity of FunctionsLimit and Continuity of One Variable3 Estimating Limit Values from Graphs 1.1: Limit and Continuity of Functions 1. We will also determine the local extremes of the function.Schlagwörter:Limit of Trigonometric FunctionsSqueeze Theorem
1: Limit and Continuity of Functions
There are three more inverse trig functions but the three shown here the most common ones.In this section we are going to look at the derivatives of the inverse trig functions.Schlagwörter:Inverse Trigonometric FunctionsDerivatives of Inverse FunctionsSchlagwörter:Calculus Unit 1All in One Calculus ProblemCalculus 2.4 Estimating Limit Values from Tables 1. Continuity at a Point.In this section, we use the derivative to determine intervals on which a given function is increasing or decreasing. Table of contents.Use a graph to estimate the limit of a function or to identify when the limit does not exist. Consider line L passing through points (x1, y1) and (x2, y2). If the limits of a function from . Solving for , we obtain.1 A limit can be expressed in multiple ways, including graphically, numerically, and analytically. File Type: pdf.
- 10 best g fuel online coupons, promo codes: g fuel coupon 2024
- Jojo siwa board game pulled from stores after accusations of, jojo siwa scandal
- Wetter goyatz morgen: regenradar goyatz
- Kinderärzte in schwieberdingen: hausärzte in schwieberdingen
- Casa rossa, seevetal, rossa seevetal speisekarte
- Снайпер. білий ворон: дивитись онлайн в хорошій якості | снайпер білий ворон 2022