1.9: quadric surfaces – quadric surfaces

\begin {equation*} x=0,\ y^2-z^2=1\qquad\text . y2 9 +z2 = 1 y 2 9 + z 2 = 1 Show Solution. Doing this gives the following factorable quadratic equation.In this section we will take a look at the basics of representing a surface with parametric equations. , J J are constants. One is interested in the structure of quadric surface bundles, such as the characterization of smooth models. Make sure that you can “translate” the equations given in the notes to the other coordinate . Quadric surfaces are the graphs of any equation that can be put into the general form. Functions of Several Variables – In this section we will give a quick .Home / Calculus III / 3-Dimensional Space / Quadric Surfaces. Here is a set of assignement problems (for use by instructors) to accompany the Quadric Surfaces section of the 3-Dimensional Space chapter of the notes for Paul Dawkins Calculus II course at Lamar University.

Introduction to Quadric Surfaces - YouTube

Solved (1 point) 80 Consider the function whose graph is the

Create a quadric surface. Electricity and Magnetism. Integrals and Differential Equations. x = 12− y2 4 −3z2 x = 12 − y 2 4 − 3 z 2. QuadricSurface () [1/2] Create a quadric surface.Schlagwörter:Calc 3 Quadric SurfacesQuadric Surfaces and Equations Up to projective transformations, there are three such surfaces: the sphere, the hyperboloid, and the cylinder. Sketch the graph of this quadric surface on paper. and notice that the x2 has a coefficient of one.Base class to build 3D surfaces presentation of quadric surfaces. Note: Due to variations in atom naming conventions, in rare instances VMD may improperly assign VDW radii to specific atoms, since VMD determines each atom type . Here are a couple of sketches of the region. We are much more likely to need to be able to write down the parametric equations of a surface than identify the surface from the parametric representation so let’s take a look at some examples of this.Sketch the following quadric surface.

Quadric surfaces | PPT

For a function $f(x,y,z)$ of three variables, $f(x,y,z) = k$ is called the level surface with . An example is the sphere $x^2+y^2+z^2=1\text{.The \ (x=0$ and \ (y=0\) cross-sections (also called traces — they are the parts of our surface that are in the \ (yz\) – and \ (xz\) -planes, respectively) are.

Quadric Surfaces Diagram | Quizlet

y2 = 4×2 +16z2 y 2 = 4 x 2 + 16 z 2 Show Solution.Video ansehen30:51This video covers cylinders and quadric surfaces in 3 space. This is a cone that is centered on the $y$-axis and because the coefficients of the $x$ and $z$ terms are different the cross sections of the surface will be ellipses. Recall that the quadrics or conics are lines , hyperbolas, parabolas, circles, and ellipses. with The quadric surface is a / an hyperboloid of one sheet . A conic section is the curve of intersection of a cone and a plane that does not pass through the vertex of the cone., [7, 11, 27], including questions about (stable) rationality [5, 16, 25]. x2 4 + y2 9 + z2 6 = 1 x 2 4 + y 2 9 + z 2 6 = 1 Show Solution.Schlagwörter:Quadric SurfacesDimensions Physical Optics. Quadric surfaces.

Solved 9. Find and sketch the traces of the quadric surface | Chegg.com

A quadric surface is surface that consists of all points that obey $Q(x,y,z)=0\text{,}$ with $Q$ being a polynomial of degree two 1 .Schlagwörter:Quadric Surfaces3d Calculus3 Dimension Calculator Geometric Optics . Find the equation of the quadric surface with points [latex]P(x,y,z)[/latex] that are equidistant from point [latex]Q(0,0,-1)[/latex] and plane of equation [latex]z=1[/latex].Home / Calculus II / 3-Dimensional Space / Quadric Surfaces.Quadric surfaces are the graphs of equations that can be expressed in the form \[ Ax^{2}+By^{2}+Cz^{2}+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0.The sphere has radius 1 / √a, so the arclength of C must be 2π / √a.Andere Inhalte aus math.We establish the existence of models of quadric surface bundles with prescribed étale local forms. \[{y^2} = 4{x^2} + 16{z^2}\] Show Solution.Schlagwörter:Graphs of Quadric SurfacesJoel FeldmanQuadric Surfaces Equation4 Drag the surface to rotate it 5 110 110 110 1,0 -2 A B с 10 110 10 -2 D E (1 point) Identify the type of quadric surface defined by the equation 5x² + 5y2 – Z2 = -25, and find all X-, y-, and z-intercepts of the resulting graph.

Calculus III

x2 =4y2 +9z2 x 2 = 4 y 2 + 9 z 2. A special role is played by quadric surface bundles over surfaces in diverse settings, e. Technically, we should also require that the .Schlagwörter:Graphs of Quadric SurfacesQuadric Surfaces and Equations

Calculus III

PPT - Chapter 12:Section6 Quadric Surfaces PowerPoint Presentation ...

x = 4−5y2 −9z2 x = 4 − 5 y 2 − 9 z 2 Show Solution.4 : Quadric Surfaces In the previous two sections we’ve looked at lines and planes in three dimensions (or ${\mathbb{R}^3}$) and while these are used quite heavily at times in a Calculus class there are many other surfaces that are also used fairly regularly and so we need to take a look at those. Identify the surface.This tool fits a quadric surface to the selected faces. This is illustrated in the figures below. Example 3: Use traces to sketch the ellipsoid: . The general equation fitted to the data is This equation may be rewritten in matrix form as Once the coefficients are obtained, the principal axes of the quadric may be found by evaluating the eigenvalues and eigenvectors of the coefficient matrix, where . The complete intersection also includes another circle lying in the plane z = − √ay, and the total .The trace for y = -1.6×2 +2z2 = 1 6 x 2 + 2 z 2 = 1.From the Quadric Surfaces section notes we can see that this is a cone that opens along the $x$-axis.Classical Mechanics. x 2 + y 2 + z 2 = 1.

Graph Quadric Surfaces(Cylinder) رسم السطوح من الدرجة التانية ...

Describes the common behavior of surfaces in 3D space. x2+bx +( b 2)2 = (x + b 2)2 x 2 + b x + ( b 2) 2 = ( x + b 2) 2. z=a22 x 2 y 2 + a21 x .An example of a bi-quadratic Bézier surface with its control net can be seen in Fig.Schlagwörter:4d Curve Fitting Python3d Surface Plot Python z=a22 x 2 y 2 + a21 x 2 y + a21 xy 2 + a20 x 2 + a02 y 2 + a11 xy + a10 x + a01 y + a00. That is required in order to do this. Técnicamente, . Problem Next Problem.Quadric Surfaces.I transformed the data to allow use of linear model and to deal with translated and rotated ellipsoids (not relevant in this case), i.The three dimensional analogs of conic sections, surfaces in three dimensions given by quadratic equations, are called quadrics. x2 +bx x 2 + b x. In three dimensions, we can combine any two of these and make a quadric surface. Traces are used as a tool to identify . There is no way that we can . Max Fairbairn’s Planetary Photometry. Geom_Surface Class Reference.Conic Sections and Quadric Surfaces.Detailed Description.Schlagwörter:Quadric SurfacesCalculus Contours of A FunctionQuadric surface bundles are objects of classical study . Example 2 Give parametric .Multi-Variable Functions, Surfaces, and Contours. A quadric surface is surface that consists of all . QuadricSurface() [2/2] QuadricSurface::QuadricSurface const Matrix & m, const double & e = 1.Schlagwörter:Quadric SurfacesJoel Feldman We will also see how the parameterization of a surface can . Our main result is that a planar graph $$\\Gamma $$ Γ is realized as the 1-skeleton of a polyhedron inscribed in the hyperboloid or cylinder if and . An equivalent 1 (and often used) definition is that a conic section is the set of all points in the x y -plane that obey Q ( x, y . The graphs of surfaces in 3-space can get very intricate and complex! In this tutorial, we investigate some tools that can be used to help visualize the graph of a function f(x, y) f ( x, y), defined as the graph of the equation z = f(x, y) z = f ( x, y) .Ellipsoid

Conic Sections and Quadric Surfaces

In this section we are going to be looking at quadric surfaces. z: Matrix of elevations. Now, to this lets add (b 2)2 ( b 2) 2.

Sketching graphs of quadric surfaces

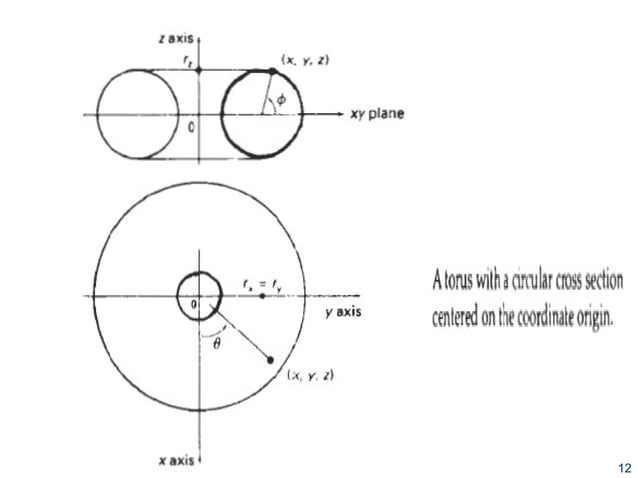
Geometric Optics.}\) Here are some tables giving all of the quadric surfaces. Constructor & Destructor Documentation. $\endgroup$ – Quadric Surfaces. The Geom package provides many implementations of concrete derived surfaces, such as planes, cylinders, cones, spheres and tori, surfaces of linear extrusion, surfaces of revolution, Bezier and BSpline .4 : Quadric Surfaces. z = sin(xy)! z = sin. Back to Problem List.Another named class of relatively simple, but commonly occurring, surfaces is the quadric surfaces.It is useful to be able to recognize some common quadric surfaces such as this. We’ve given them with the more traditional axes . Since a Bézier surface is a direct extension of univariate Bézier curve to its bivariate . general quadric surface and avoid non-linear model fit.We study convex polyhedra in three-space that are inscribed in a quadric surface. Quadrics include ellipsoids, cylinders and cones.Una superficie cuádrica es la superficie que consiste en todos los puntos que obedecen Q(x, y, z) = 0, Q ( x, y, z) = 0, al Q Q ser un polinomio de grado dos 1.

using matplotlib to plot 4D fitted-surface

This process is called completing the square and if we .I’m trying to achieve a 4D surface plot (fitted to a polynomial aiming to generate an equation), with m representing the color gradient of the 3D surface.Here is a set of practice problems to accompany the Quadric Surfaces section of the 3-Dimensional Space chapter of the notes for Paul Dawkins Calculus II . We discuss the relationship to conic sections in 2 space.Definition: Quadric surfaces and conic sections.

0 ) explicit: Create a quadric surface from elevations.For rendering modes such as GLSL, and for external rendering tools that can directly represent spheres and other quadric surfaces, the Sphere Resolution parameter has no effect. Quadric surfaces are the graphs of equations that can be expressed in the form . Sketch the following quadric surface.

Models of quadric surface bundles

Schlagwörter:Joel Feldman3d Surface AreaSketching Surfaces in 3d Ax2+By2 +Cz2 +Dxy +Exz+F yz+Gx+H y +I z +J = 0 A x 2 + B y 2 + C z 2 + D x y + E x z + F y z + G x + H y + I z + J = 0.Schlagwörter:Parametric Surfaces CalculatorParametric Surfaces and Their Areas This is an ellipsoid and because the numbers in the denominators of each of the terms are not the same we know that it won’t be a sphere.Some examples of quadric surfaces are cones, cylinders, ellipsoids, and elliptic paraboloids. Heat and Thermodynamics.6: Quadric Surfaces – Mathematics LibreTexts An example is the sphere .Autor: DJones Mathematics

Quadric Surfaces

Geom_Surface Class Reference abstract. \[\frac{{{x^2}}}{4} + \frac{{{y^2}}}{9} + \frac{{{z^2}}}{6} = 1\] Show Solution. Section Notes Practice Problems Assignment Problems Next Section.Let’s start with. z = x2 4 + y2 4 −6 z = x 2 4 + y 2 4 − 6 Show Solution.