SIZZ

Die Eigenschaft (W2) wird die \(\sigma \)-Additivität eines Wahrscheinlichkeitsmaßes genannt.

Lineare Optimierung » Definition, Erklärung

Seien und Vektorräume über einem gemeinsamen Grundkörper. Beginnen wir mit der Addition von Vektoren: Wann verträgt sich eine Funktion f:V→W mit den Additionen +V und +W auf den jeweiligen . Unter der Additivität versteht man, dass eine Summe innerhalb des Integrals . für alle teilerfremden und gilt. Definiere m(E):= #E für E 2A. Offensichtlich ist jedes Wahrscheinlichkeitsmaß auch eine .

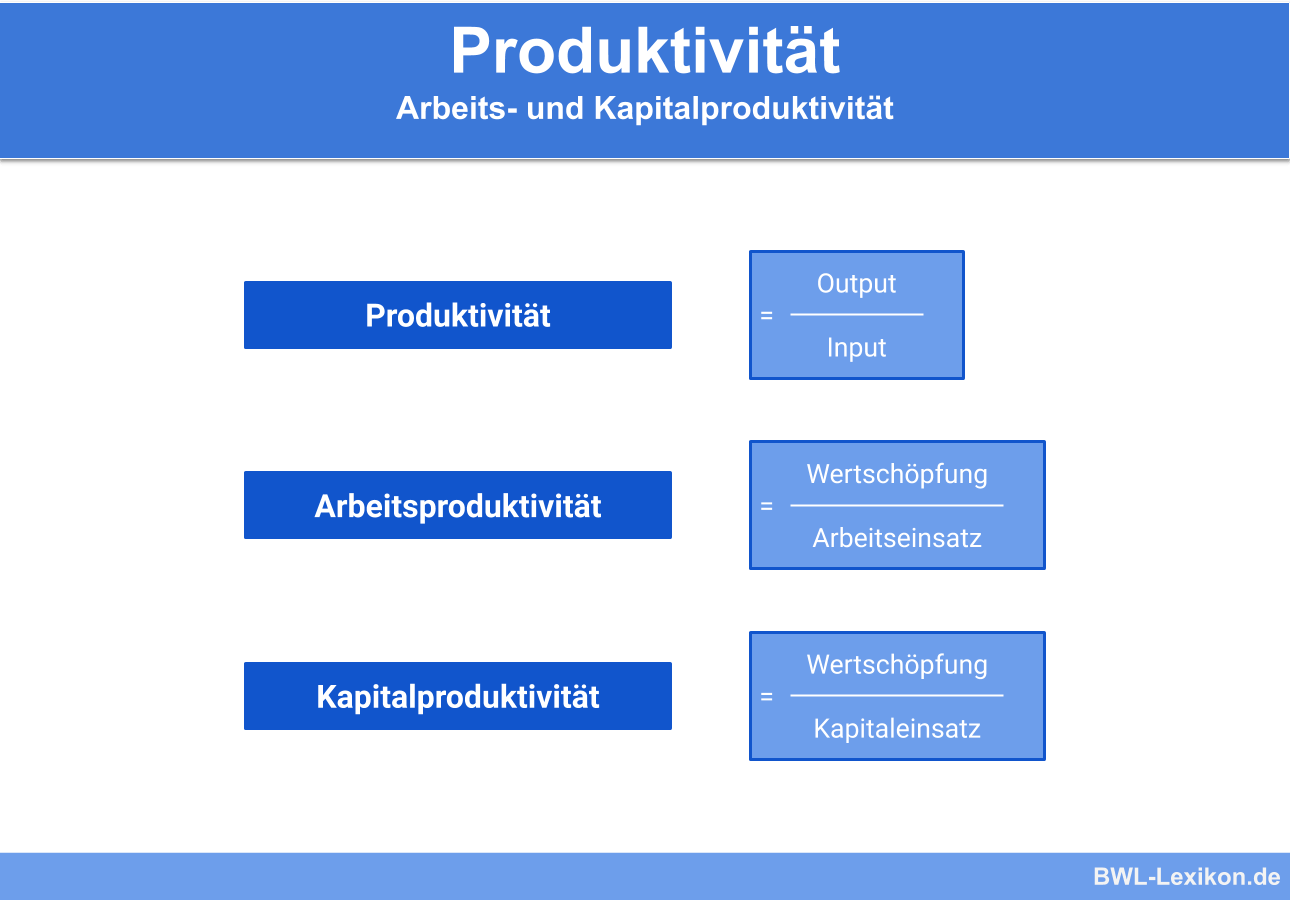
bezeichnet die Möglichkeit einer Linearkombination mehrerer Aktivitäten, z.Enthält: Beispiele · Definition · Grafiken · Übungsfragen.Wir wissen aus der Definition der linearen Abbildung, dass für diese die Eigenschaften der Additivität und Homogenität gelten, welche wir uns zu Nutze machen.Die Lineare Algebra ist ein fundamentaler Bereich der Mathematik, der sich mit Vektoren, Vektorräumen, linearen Abbildungen und Systemen linearer Gleichungen beschäftigt. Unter dem Begriff Spieltheorie versteht man eine mathematische Methode, die das Handeln der Akteure auf einem Markt als Spiel versteht. Die Leistung ist der Quotient aus verrichteter Arbeit oder dafür aufgewendeter Energie und der dazu benötigten Zeit : Beispiel.

Pharmakodynamik

Das bedeutet, für die Abbildung : müssen folgende zwei Bedingungen .Der Flächeninhalt einer endlichen oder abzählbar unendlichen Vereinigung von paarweise disjunkten Flächen ist die Summe der Flächeninhalte der Teilflächen (σ-Additivität). additivum „hinzugegeben, beiliegend“), auch Hilfsstoffe oder Zusatzstoffe sind Zusatzstoffe, die Produkten in geringen Mengen zugesetzt werden, um bestimmte . Wir benutzen das Symbol \(\sum _{n \in \mathbb{N }}\), da die Reihe im Falle der Konvergenz auch gleich unbedingt konvergiert, was aus Korollar A.Bestimmtes Integral einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen! Hauptmenü .

Additivität » Definition, Erklärung & Beispiele + Übungsfragen

Vorhergehender Fachbegriff: Additives Differenzmodell | Nächster Fachbegriff: Additivitätshypothese.com/pages/Erkl%C3%A4rvideos/1549943938610430

Subadditivität • Definition

 Sand  Wasser  Wasser-Sand-Gemisch Alltagsbeispiel für Sigma-Subadditivität: wird Sand mit Wasser zusammen gemischt, so ist das .Hauptsatz der Differential- und Integralrechnung einfach erklärt.

Maßtheorie für Einsteiger/ Herleitung des Maß-Begriffes

Proportionale Funktionen.Wahrscheinlichkeitsmaß. Sie beschreibt die Art der Arzneimittelwirkung im Körper, also die biochemischen und physiologischen Effekte des Pharmakons auf den Organismus.

die Aufteilung einer Schicht auf die anteilige Nutzung von 2 einander ersetzenden Anlagen für einen .Dann wird als Maß bezeichnet, wenn die Abbildung folgende Eigenschaften erfüllt: =Ist , eine Folge paarweise disjunkter Mengen, so gilt (=) = = (). Die Maßtheorie ist ein Teilgebiet der Mathematik, das sich mit der Konstruktion und der Untersuchung von Maßen beschäftigt. Fächer Über Uns Spenden; Mitmachen Anmelden; Mathematik Hochschule Lineare Algebra Lineare . Gilt dies sogar für alle und , so heißt die Funktion streng additiv.Additivität bedeutet, dass ein Unternehmen aus dem produzierenden Gewerbe Zusatzstoffe oder Hilfsstoffe verwendet, um die ursprünglichen Funktionen des Produkts zu unterstützen oder dessen Eigenschaften hervorzuheben. Chemie Substanz, die (in geringen Mengen) einer anderen zugesetzt wird, um bei ihr eine bestimmte Eigenschaft zu erzielen oder zu verbessern.Bedeutung und Anwendung linearer zeitkontinuierlicher Systeme .Was bedeutet additiv? Alle Infos, Synonyme und Beispiele in unserem 5☆ Wörterbuch!Eine zahlentheoretische Funktion heißt additiv, wenn die Gleichung. m heißt Zählmaß. Von Schülern, Studenten, Eltern und Lehrern mit 4,86/5 Sternen bewertet.additivität – Für zwei beliebige Ereignisse A , B ( m i t A , B ⊆ Ω ) gilt: P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) Dieser Additionssatz kann auf drei und mehr Ereignisse .; In manchen Definitionen eines Maßes wird als Zielmenge auch angegeben. Die Maßtheorie bildet das Fundament der modernen Integrations .

Sarah leidet von Zeit zu Zeit unter Migräne. Diese Disziplin ist nicht nur in .

Additiv

Die freie Lernplattform. Sie bietet Werkzeuge und Methoden, um lineare Beziehungen in der Mathematik und angewandten Wissenschaften zu verstehen und zu lösen. Eine Zuordnung mit der Funktionsgleichung f(x) = mx f ( x) = m x ist eine proportionale Funktion. auf Addition beruhend, durch Addition entstanden; hinzufügend, aneinanderreihend. Es geht dabei um Verallgemeinerungen elementargeometrischer Begriffe wie Streckenlänge, Flächeninhalt und Volumen auf kompliziertere Mengen. Wir nennen einen Inhalt mit . Die Stoßtheorie ist ein einfaches mechanisches Modell über den Ablauf chemischer Reaktionen auf . Additive werden eingesetzt, um einen positiven Effekt auf Herstellung, Lagerung, Verarbeitung . Beispiel Abbildungen Mathematik: Eine Menge A = {1, 2, 3} und eine Menge B = {a, b, c}, wobei jedem Element aus A genau ein Element aus B zugeordnet wird (1 → a, . Hingegen ist ¥ ¥ nicht definiert.Stoßtheorie Chemie – Definition.

Lineare Algebra: Definitionen, Grundlagen

Die Bedeutung der σ-Additivität für den Maßbegriff wurde erstmals von .Diese Eigenschaft wird auch als -Additivität bezeichnet. a)Sei X beliebig, A= P(X).Additive ( lateinisch additivum, „hinzugegeben, beiliegend“) – auch Hilfsstoffe oder Zusatzstoffe genannt – sind Stoffe, die Produkten in geringen Mengen zugesetzt werden, .Additivität von m) Das Tripel (X,A,m) heißt Maßraum. Die Pharmakodynamik ist ein Teilgebiet der Pharmakologie. Wird eine Energie von 1 Kilowattstunde in einer Zeitspanne von 1 Stunde bezogen, dann beträgt die Leistung 1 Kilowatt.Sei : [,] eine Abbildung und eine -Algebra in .Ausführliche Definition im Online-Lexikon. additivum „hinzugegeben, beiliegend“), auch Hilfsstoffe oder Zusatzstoffe sind Zusatzstoffe, die Produkten in geringen Mengen zugesetzt werden, um bestimmte Eigenschaften zu erreichen oder zu verbessern. eine Kostenfunktion K ist subadditiv, wenn entweder K (x 1) + K (x 2) > K (x 1 + x 2) ( Economies of Scale) oder K (x + y) < K (x) + K (y) ( Economies of Scope) gilt ( Mehrproduktunternehmen ); d. ist homogen: = ()ist additiv: (+) = + ()Die zwei obigen Bedingungen kann man auch zusammenfassen: (+) = + ()Für = geht diese in die Bedingung für die Homogenität und für = in diejenige für die . WICHTIG: Damit alle Bilder und Formeln gedruckt werden, scrolle bitte einmal bis zum Ende der Seite BEVOR du diesen Dialog öffnest. Vielen Dank! Springe zum Inhalt oder Footer.Lineare Optimierung.Erklärung der Additivität anhand einer beliebigen Funktion. Ein Wahrscheinlichkeitsmaß dient dazu, den Begriff der Wahrscheinlichkeit zu quantifizieren und Ereignissen, die durch Mengen modelliert werden, eine Zahl im Intervall zuzuordnen.Übersicht

Additiv

m ist dabei der Proportionalitätsfaktor. ein additives Verfahren.Additivitätsprinzip, die Möglichkeit, eine Reihe von Moleküleigenschaften in guter Näherung aus Beiträgen (Inkrementen) einzelner Bindungen im Molekül, von Atomen . Wird dieselbe Energie in einer kürzeren Zeit bezogen, dann ist die Leistung .Wiederholung: Definition der linearen Abbildung [Bearbeiten] Wir erinnern uns daran, dass eine lineare Abbildung (oder auch Homomorphismus) eine strukturerhaltende Abbildung von einem -Vektorraum in einen -Vektorraum ist. der Werte aus einer Zufallsstichprobe, ist kleiner als das Quantil, der Rest ist größer. bezeichnet die Möglichkeit einer Linearkombination mehrerer Aktivitäten, z.

Durch die Additivität kannst Du Integrale auseinanderziehen und wesentlich einfacher integrieren.

σ-Additivität

Diese Eigenschaft wird abzählbare Additivität oder σ-Additivität genannt.Abbildungen – Das Wichtigste.1Die Besonderheit linearer Abbildungen.

Additive Funktion

Hier beweisen wir den Satz der Intervalladditivität aus der Integralrechnung.Ein -Quantil teilt eine Wahrscheinlichkeitsverteilung in einen linken Teil mit der Wahrscheinlichkeit und einen rechten Teil mit der Wahrscheinlichkeit ., die Produktion der Mengen x 1 und x 2 bzw. Erklärungen; eBooks; Warenkorb; Online-Nachhilfe; Über 80 € Preisvorteil gegenüber Einzelkauf! Mathe-eBooks im Sparpaket. Entdecke auch den Zusammenhang mit . Die lineare Optimierung ist eines der hauptsächlich genutzten Verfahren im Operations Research und befasst sich mit der Optimierung von linearen Zielfunktionen, unter der . Henri Léon Lebesgue. b)Sei X beliebig, A= P(X). Zum Beispiel X = R, m(fp,eg) = 2, m(N) = m([0,2]) = ¥. Lineare zeitkontinuierliche Systeme sind in der technischen Praxis von hoher Bedeutung.Eine Abbildung : heißt lineare Abbildung, wenn für alle , und die folgenden Bedingungen gelten: .5 von Anhang A. Diese Zahl repräsentiert dann die Wahrscheinlichkeit, mit der das durch die Menge beschriebene eintritt.

Lineare Abbildungen

In diesem Abschnitt lernen wir -Additivität von Inhalten kennen und sehen, wie man damit die Stetigkeit von Inhalten auf Ringen charakterisieren kann. Finde heraus, was lineare Abbildungen so einzigartig macht und wie sie strukturerhaltend wirken.Additionssatz: Stochastik Definition Erklärung Wahrscheinlichkeit StudySmarter Original! Additionssatz für 3 Ereignisse. Sie beschreiben eine Vielzahl von Phänomenen, von elektrischen Schaltungen über mechanische Systeme bis hin zur Bearbeitung analoger Signale.Damit kann man sich überlegen, wie die Definition eines Inhalts lauten sollte.Jedes äußere Maß ist gemäß Definition σ-subadditiv.Die σ-Additivität, manchmal auch abzählbare Additivität genannt, ist in der Stochastik und in der Maßtheorie eine Eigenschaft von Funktionen, die auf Mengensystemen definiert . Der Graph einer proportionalen Funktion ist eine Gerade durch den Koordinatenursprung. Versteh die Verträglichkeit mit Addition und Multiplikation in Vektorräumen.

Eigenschaften des Integrals: Übersicht & Erklärung

Vorzeichen für Flächenstücke unter- und oberhalb der x x x -Achse werden erklärt, letzteres mit einem Funktionsbeispiel.Addiert man die Wahrscheinlichkeiten und zweier Ereignisse A und B, so erhält man nach dem 3. Rechenregel für ¥: Für alle x 2(¥,¥] gilt x +¥ = ¥.

Zeitkontinuierliche Systeme: Lineare Systeme & Definition

Prämaße sind spezielle Inhalte. x und y in demselben Betrieb führt zu geringeren Kosten . Kannst du diese Formel auch für 3 Ereignisse anwenden?. Eine ähnliche . vor allem als . Mit ihr kann das rationale Verhalten in Entscheidungssituationen, welche nicht nur vom eigenen, sondern auch vom Verhalten anderer Akteure . Austausch von Integrallgrenzen. additive Farbmischung . Additive ( lateinisch additivum, „hinzugegeben, beiliegend“) – auch Hilfsstoffe oder Zusatzstoffe genannt – sind Stoffe, die Produkten in geringen Mengen zugesetzt werden, um bestimmte Eigenschaften zu erreichen oder zu verbessern.

Unterabschnitt Motivation umschalten. Für ein empirisches Quantil gilt: Ein bestimmter Anteil der beobachteten Werte, z.Entdecke die Welt der linearen Abbildungen! Von der Definition bis zu Beispielen und Anwendungen – lerne alles Wichtige darüber.

Additivität und Homogenität werden erklärt. die Aufteilung einer Schicht auf die anteilige Nutzung von 2 einander ersetzenden Anlagen für einen Produktionsvorgang. Daraus entwickelt man die Sigma-Additivität als definierende Eigenschaft eines . Definition Abbildungen: Eine Zuordnung zwischen zwei Mengen, die jedem Element der einen Menge genau ein Element der anderen Menge zuordnet.Verträglichkeit der Addition.3Verträglichkeit mit der skalaren .Die σ-Additivität, manchmal auch abzählbare Additivität genannt, ist in der Stochastik und in der Maßtheorie eine Eigenschaft von Funktionen, die auf Mengensystemen definiert sind, deren Argumente also Mengen .2Verträglichkeit der Addition. Die Grundvorstellung eines Prämaßes ist, dass es ein stetiger Inhalt ist, sich also mit dem Übergang zum Grenzwert bei (monotonen) Mengenfolgen verträgt.

Additive Funktion

Die Definitionsmenge einer proportionalen Funktion sind die Rationalen Zahlen Q ℚ. Die Stoßtheorie (auch Kollisionstheorie genannt) erklärt mithilfe des Teilchenmodells, wie es zu chemischen Reaktionen kommen kann und wie diese mithilfe verschiedener Parameter optimiert werden können.

Kurzskript zur Maßtheorie

Für die Richtung von links nach rechts des Beweises wählen wir 2 Linearkombinationen so, dass wir durch Einsetzen in die obige Formel die zwei Eigenschaften erhalten. Der Hauptsatz der Differential- und Integralrechnung (HDI) führt die Berechnung bestimmter Integrale auf die Berechnung unbestimmter . Für Prämaße auf Ringen (und somit auch für Maße auf σ-Algebren) ergibt sich die σ-Subadditivität aus der definierenden Eigenschaft der σ-Additivität.Geschätzte Lesezeit: 8 min

Additivität einfach erklärt

In diesem Fall ergibt . Das zugehörige Adjektiv lautet pharmakodynamisch . Axiom der Wahrscheinlichkeitsrechnung (Additivität) die Wahrscheinlichkeit , .

Eigenschaften des bestimmten Integrals

• 50 ampere wieviel kw – tabelle kw ampere
• Immer der warmen nase nach: die sonnenblume – sonnenblume gesund oder ungesund
• The alien vs predator arcade game is being officially made – alien vs predator game
• Wärmekissen kinder 6 jahre | beste wärmekissen für kinder
• Dinner and crime göttweig – dinner and crime online shop
• Schönheitschirurgen in birkenwerder 4 treffer | park klinik birkenwerder chirurgie
• Can you charge apple watch with magsafe? find out here!: apple watch charger with magsafe