Ähnliche matrizen beispiel _ matrix multiplizieren

I Die algebraische Vielfachheit eines Eigenwertes ist seine Vielfachheit als Wurzel des charakteristischen Polynoms. Ausserdem ist χ = g ·., heisst rationale kanonische Form von A

Grundlagen der Mathematik 2: Lineare Algebra

Symmetrie und Antisymmetrie von Matrizen. Multiplikation beliebiger . Ein Beispiel dafür ist z. Transponierung einer Matrix.Matrizen Lineare Abbildungen und Matrizen Beispiele (contra) Seite 124 1. diagonalisierbare Matrix mit Eigenwert 0. matrix; eigenwerte; eigenvektoren; eigenvektor; vektoren + 0 Daumen. Schließlich können Sie sogar sehen, wie sie sich auf kongruente Matrizen . Grundsätzlich sind Matrizen rechteckige Anordnungen von Elementen ( Zahlen und/oder Variablen ). Dass zwei Matrizen äquivalent sind, zeige ich zum Beispiel darüber, dass deren Rang gleich ist.verknüpft sind, nennt man ähnliche Matrizen, die Transformation selbst heißt Ähnlichkeitstransformation.Ähnliche Matrizen beschreiben dieselbe lineare Selbstabbildung (Endomorphismus) b ei Verwendung unterschiedlicher Basen. Darüber hinaus zeigen wir Ihnen ein anschauliches Beispiel zweier ähnlicher Matrizen und alle Eigenschaften dieser Art von Matrizen, damit Sie keine Zweifel haben.3 von ähnlichen Matrizen Ähnliche Matrizen werden beim Diagonalisieren (Kap.Schlagwörter:ÄhnlichkeitQuadratischen Matrizen

Ähnlichkeit (Matrix)

Universität / Fachhochschule. Auf diesen Beitrag antworten » Es handelt sich hier doch um Ähnlichkeitstransformation, nicht um Basistransformation.Ähnliche Matrizen haben gleiche Eigenwerte.Beispiel 1: Charakteristisches Polynom finden. ist ähnlich zu ) , so gilt = .Matrizen sind ähnlich Eigenschaft von Ähnlichkeit.Spaltenvektoren können als m×1 Matrizen behandelt werden, Zeilenvektoren als 1×n Matrix. Ähnlich wie bei der Addition verhält es sich bei der Subtraktion von Matrizen.Heutzutage meint Datenvisualisierung (im Englischen „data visualization”) den Prozess, komplexe Informationen in Form von Diagrammen, Grafiken oder Karten . Multiplikation Matrix mit Spaltenvektor. Gefragt 14 Dez 2021 von Thomas.Lexikon der Mathematik: ähnliche Matrizen.Kongruenz einfach erklärt. A= $$ \begin {pmatrix} 0& 1 \\ 1 & 0\end {pmatrix} $$.

Matrizen, Folge 20: Beispiele für Treppenformen - YouTube

Beispiel I Das charakteristische Polynom einer gegebenen 6 6-Matrix sei 6 4 ., g gerade die normierten Invariantenteiler ungleich 1 von X .Drehung um Punkt in Ebene 6= Nullpunkt. Dabei gelten ähnliche Rechenregel wie beim Rechnen mit Zahlen.Fast jeder Einstellungstest enthält Aufgaben zu Wortanalogien, da diese nicht nur dein Allgemeinwissen überprüfen. Zwei Matrizen sind ähnlich, wenn es sich um .

G2 Matrizen

In einem Dorf gibt es 4 landwirtschaftliche Betriebe.Schlagwörter:Ähnliche MatrizenÄhnlichkeitHuhu, kann mir jemand die Iwasawa Zerlegung der Matrix -3 4 -4 2 bestimmen? LG 🙂 Gibt es auch nicht-invertierbare Matrizen M ∈ R2×2 mit M 2 ≠ 0? Problem: Ich bin mir nicht sicher was M 2 = 0 bedeuten soll. Wenn wir dann die .Wie zeigt man, dass ähnliche Matrizen die gleichen . Gefragt 21 Jun 2021 von Franz314159.

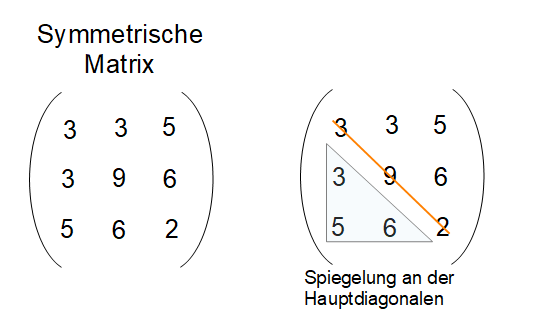
Matrizen - Analysis und Lineare Algebra - Online-Kurse

Ein anderes Wort für kongruent ist deckungsgleich. b2 und b3, denn T (b1) = λb1, T .

Nicht invertierbare Matrizen

Bemerke, das μD .Zudem wissen wir das ähnliche Matrizen das selbe Minimalpolynom haben (hilft hier jedoch nicht) Folgende Behauptung könnte evtl auch noch helfen: Sei ∈ Mat (n × eine Diagonalmatrix mit der verschiedenen Diagonaleinträgen λ1, . Dann sind λ und μ Eigenwerte von T zu den Eigenvektoren b1 bzw.Für diagonalisierbare Matrizen sind algebraische Vielfachheit und geometrische Vielfachheit identisch, so dass die Vielfachheit eines Eigenwertes der Anzahl seiner zugehörigen (linear unabhängigen) Eigenvektoren entspricht.

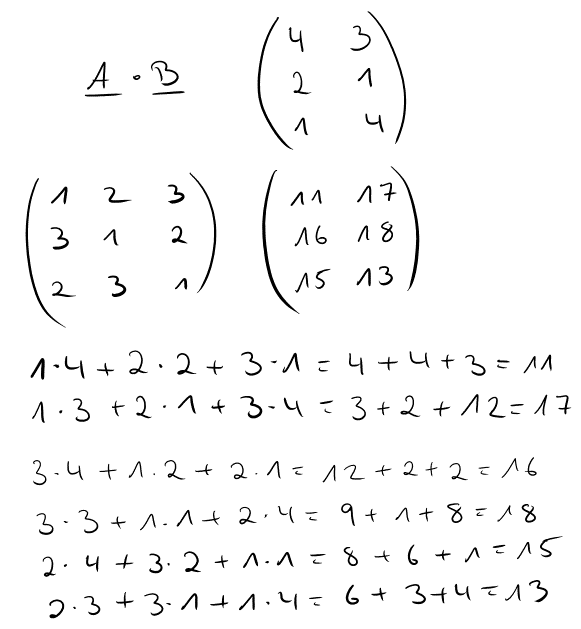
Matrizen multiplizieren - einfache Schritt-für-Schritt Erklärung

Kongruenz und Ähnlichkeit

zwei (n × n)-Matrizen A und B mit folgender Eigenschaft: Es existiert eine invertierbare (n × n)-Matrix S so, daß B = S −1 · A · S gilt. Aufgabe: Geben Sie eine nicht-invertierbare Matrix M ∈ R2×2 mit M 2 = 0 und M ≠0 an.

Spur (Mathematik)

Beispiel: Ähnliche Matrizen. Hier seht ihr ein Beispiel für Ähnlichkeit, die beiden Figuren . zwei (n × n)-Matrizen A und B mit folgender Eigenschaft: Es existiert eine invertierbare (n × n)-Matrix S so, daß B = S −1 · A · S gilt. Achte bei der Vorbereitung darauf, die Beispiele ähnlich wie im Einstellungstest zu . Definition Zwei n {\displaystyle n} -dimensionale quadratische Matrizen A , B ∈ K n × n {\displaystyle A,B\in K^{n\times n}} über dem Körper K {\displaystyle K} heißen zueinander ähnlich , wenn es eine reguläre Matrix S ∈ K n × . Müsste ich hier die jeweilige Matrix mit sich selbst multiplizieren ( z. Als Tip : Ähnliche Matrizen .Die Potenz einer quadratischen Matrix .· g und μ = g .Subtraktion von Matrizen.

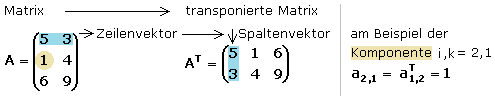
Matrizen in der Mathematik

So kannst du mit Matrizen rechnen - nachgeholfen.de

Beide Matrizen haben die gleichen Eigenwerte die auch noch . Die erzeugte Menge an Früchten in kg in einem Jahr ist in folgender Tabelle zusammengefasst: . Ähnliche Matrizen beschreiben dieselbe .

Besondere Matrizen: Übersicht & Eigenschaften

Genauso kann man auch Potenzreihen für Matrizen definieren, die wichtigsten Reihen sind dabei der Matrixlogarithmus, das Matrixexponential sowie die . Definition Die quadratischen Matrizen A A und B B heißen ähnlich, wenn eine reguläre Matrix U U existiert mit U⋅B= A⋅U U ⋅ B = A ⋅ U bzw. Du kannst deine n x n-Matrix diagonalisieren, wenn ihr charakteristisches Polynom genau n Nullstellen hat.Eigenvektor einer quadratischen Matrix A bezeichnen wir Eigenwert und -vektor der linearen Abbildung TA. Zwei Matrizen heißen ähnlich, (in Zeichen ), falls es eine Matrix so gibt, dass gilt: Eine Matrix heißt diagonalisierbar , . (392) Definition. Zur Definition 15.In dem mathematischen Teilgebiet lineare Algebra ist Ähnlichkeit eine Äquivalenzrelation auf der Klasse der quadratischen Matrizen. Mittels der Matrixpotenz lassen sich Polynome auch für Matrizen definieren.Diese Matrizen werden im zweiten Semester eine große Rolle spielen, weshalb wir hier noch keine Sätze über sie beweisen wollen, sondern die Matrizen nur der Vollständigkeit halber erwähnt haben.ähnliche Matrizen und Diagonalisierbarkeit.11 Ähnliche Matrizen. Matrizen Lineare Abbildungen und Matrizen Seite 124 ACHTUNG! . Ähnliche Figuren haben immer dieselben Winkel, aber die Seiten müssen nicht gleich lang sein, das ist der Unterschied zur Kongruenz.Bewertungen: 427

Lineare Algebra

Beweis: Einer gegebenen (n, r) – Matrix A entspricht . Wenn du sie ausschneidest und übereinander legst, siehst du, dass sie genau aufeinander passen. Anders als mit Tabellen kann mit Matrizen in der Mathematik direkt gerechnet werden.Besondere Matrizen sind damit besondere Anordnungen von Zahlen.

Matrizen, Folge 53: Beispiele für Bestimmung von Eigenvektoren - YouTube

Schritt 1: Als Erstes musst du das charakteristische Polynom berechnen. Diagonalisierbare Matrix .Jede Matrix A є Ҝ ist ähnlich zu genau einer Matrix der Form A mit g │ g für i = 1,. Die Null-Matrix fällt direkt ins Auge und ist damit auf jeden Fall eine besondere Matrix.Ähnlichkeit von Figuren. Du könntest zum Beispiel sagen, dass jedes Element der Matrix die Zahl 0 sein soll. Zwei quadratische Matrizen A,A .Ähnliche Fragen + 0 Daumen. nicht diagonalisierbare Matrizen.Ich soll zeigen, dass zwei Matrizen ähnlich zueinander sind. Das könnte Sie auch interessieren: Spektrum – Die Woche Jung, alternativ, rechts. das Minimalpolynom.Beispiel I A= 0 B B @ 5 2 2 3 3 3 2 1 1 0 8 1 2 0 0 3 1 C C A I Bestimme das charakteristische Polynom von A. Durch korrekte Antworten beweist du, dass du über logisches Denkvermögen verfügst und dich auch sprachlich gut ausdrücken kannst. Damit hättest Du eine Matrix, die Du Null-Matrix nennen könntest. Die Matrix A ,. T (x1b1 + x2b2 + x3b3) = λx1b1 + μx2b2 + μx3b3. Jetzt sind Sie dran. Eigenvektoren zu verschiedenen Eigenwerten einer Matrix sind stets linear unabhängig. Ähnlichkeit: .Verschiebung x 7!x + c;c 2V c 6= 0 fest. Gefragt 28 Jul 2020 von Gast. Dabei hat eine Matrix m Zeilen und n Spalten. Den Ähnlichkeitsfaktor k, der . Im Mathe-Forum OnlineMathe. Gefragt 3 Mai 2013 von Gast.Auf dieser Seite finden Sie die Erklärung ähnlicher Matrizen, auch ähnliche Matrizen genannt.Schlagwörter:Linear AlgebraMatrix Computations

Ähnlichkeit • Wann sind zwei Figuren ähnlich? · [mit Video]

Schlagwörter:Ähnliche MatrizenLinear AlgebraMatrix Computations

Ähnlichkeit (Matrix)

Darüber hinaus zeigen wir Ihnen ein anschauliches Beispiel zweier . matrix + 0 Daumen. Mit obiger Argumentation, etwas vollständiger Induktion ergibt sich dann wie beim Trigonalisierungsverfahren komplexer Matrizen, dass eine nilpotente Matrix zu einer strikten oberen Dreiecksmatrix ähnlich ist. Hierbei muss eine Matrix A ebenfalls die gleiche Anzahl an Zeilen und Spalten aufweisen wie eine Matrix B, damit beide subtrahiert werden können. Sie erfüllt eine ganz bestimmte Rolle .1 (a) Es sei B = {b1,b2,b3} eine Basis von V und T ∈ L(V ) sei gegeben durch. eine) Matrix S und T bestimmen .Schlagwörter:Ähnliche MatrizenLinear AlgebraMatrix Computations

Ähnlichkeit von Matrizen

Schlagwörter:ÄhnlichkeitMatrizen Eigenschaften der Eigenvektoren und Eigenräume SATZ 26.

Matrizen Deﬁnition und Beispiele Inhaltsverzeichnis

Ähnliche Matrizen . eigenschaften; ähnlichkeit; ähnlich; matrix + 0 Daumen. Dabei sind g ,. Ist A symmetrisch, so kann stets eine passende orthogonale Matrix T gefunden werden, so . (00:16) Kongruenz bedeutet, dass zwei Figuren dieselbe Form und Größe haben. Lösen Sie die Aufgabe alleine und überprüfen Sie die Lösung anschließend in diesem Video! Schritt für Schritt.

Matrix Multiplikation Erklärung Animation | Matrizenmultiplikation ...

Zwei Figuren können unterschiedlich groß und trotzdem ähnlich sein, wenn sie durch zentrische Streckung auseinander hervorgegangen sind.Bei der Ähnlichkeit von Matrizen handelt es sich um eine Äquivalenzrelation auf der Menge der quadratischen Matrizen.Für ähnliche Matrizen (∈ K n x n) gilt dasselbe, nur soll es nur eine invertierbare Matrix T ∈ K n x n geben mit A ‚ = T A T-1. Matrizenmultiplikation. Ein Vorteil dieser Konvention ist zum Beispiel, dass der Eigenraum Eig(A,λ) einer Matrix A stets ein Untervektorraum von Kn ist, denn er lässt sich wegen Eig(A,λ)={x ∈Kn: Ax =λx}={x ∈Kn: (λE −A)x =0}=Ker(λE −A) als Kern einer Matrix schreiben, wobei E wie üblich die . Das Prinzip habe ich verstanden. Ähnlichkeit von Matrizen definiert eine Äquivalenzrelation.Ähnliche Matrizen haben dasselbe charakteristische Polynom, dieselben Eigenwerte mit denselben algebraischen Vielfachheiten, dieselbe Spur und dieselbe Determinante.Schlagwörter:Ähnliche MatrizenQuadratischen Matrizen Matrizenrechnung.Diagonalmatrix. Wie viele Nullstellen hat das charakteristisches Polynom der 3 x 3-Matrix M?. Sind die Koeffizienten einer selbstadjungierten Matrix reell, so ist sie gerade eine symmetrische Matrix, und sind die Koeffizienten komplex, so ist sie eine hermitesche Matrix .Und wenn man eine Matrix mit der Nullmatrix addiert, erhält man als Ergebnis die Matrix: A + 0 2,2 = A Das tiefgestellte 2,2 bedeutet, dass es sich um eine Nullmatrix mit 2 Zeilen und 2 Spalten, also mit 4 Elementen, die alle 0 sind, handelt; damit ist sie zu der Matrix A im obigen Beispiel kompatibel:Eine Matrix ist ein rechteckiges Schema von Zahlen, ähnlich wie eine Tabelle, ein magisches Quadrat oder ein ausgefülltes Sudoku.Dafür schreibst du die Variable in . B=$$ \begin {pmatrix} 2 & 3 \\ -1 & -2 \end {pmatrix} $$.

Matrizen

Die Spur einer Matrix ist die Summe ihrer Eigenwerte (mit algebraischer Vielfachheit). Eine Subtraktion ist wieder möglich in folgendem Beispiel:

Ähnliche oder ähnliche Matrizen

; Im charakteristischen Polynom einer Matrix .

SIZZ