Alternative sinus- und kosinusfunktionen, sinus und kosinusfunktionen berechnen

Die Trigonometrie macht sich die Ähnlichkeit von Dreiecken zunutze.

Sinus, Kosinus und Tangens

Das heißt, sie ist doppelt so groß wie bei der normalen Sinusfunktion. Er misst an einem Tag jede Stunde den . Alles, was du brauchst, um bei deinen Prüfungen zu glänzen. Daher macht es Sinn, auch die berühmte Kreiszahl rein analytisch zu .

Ableitung Sinus • Sinus ableiten mit der Kettenregel

Alternative Sinus- und Kosinusfunktionen

x k = π + k ⋅ 2 π. Suche als Erstes den Startpunkt deines Graphen; dieser liegt bei π \mathrm\pi π.Vor Tangens und Kotangens, Sekans und Kosekans bilden sie die wichtigsten trigonometrischen Funktionen.Frohn, Daniel, and Salle, Alexander.Dieser umfasst fünf Schritte: (1) Festlegung zentraler Konzepte, zu denen Grundvorstellungen formuliert werden sollen, sowie weiterer Richtlinien für den . Genauer gesagt kannst du mit den trigonometrischen Funktionen also die Winkel von . Sie strecken bzw. Die ersten beiden Grundvorstellungen zu Sinus und Kosinus beziehen sich auf rechtwinklige Dreiecke, die darauffolgenden .Aufgaben zu Sinussatz und Kosinussatz. Schritt 2: Bestimme die Ableitung der Funktion im Sinus: Die beiden Winkelfunktionen Sinus und Cosinus lassen sich nicht nur als Längenverhältnisse in einem rechtwinkligen Dreieck, sondern auch als Streckenanteile interpretieren.

Transferprozeese am Einheitskreis

Finja findet das merkwürdig, denn eigentlich haben die Kosinus- und Sinusfunktionen nur Werte zwischen -1 und 1.

Trigonometrische Funktionen — Grundwissen Mathematik

Sin Θ ist einfach nur die y-Koordinate. Sinus- und Kosinusfunktionen.Betrachte den Ausschnitt der Kosinusfunktion. Ein Winkel lässt sich sowohl im Bogenmaß (rad), als auch im Gradmaß (°) angeben. cos Θ ist einfach nur die x-Koordinate. Die hyperbolischen Funktionen traten in ihren Grundlagen implizit u.

Hyperbolische Funktionen (Hyperbelfunktionen)

Wir schauen uns jetzt eine neue Art von trigonometrischen Aufgaben an.Erstelle Lernmaterialien über Ableitung trigonometrische Funktionen mit unserer kostenlosen Lern-App! Sofortiger Zugriff auf Millionen von Lernmaterialien. und auch Sinus- und Kosinusfunktionen im Einheitskreis und im .Die Sinusfunktion ist die eindeutige Zuordnung, die jedem Winkel α α die y-Koordinate des zugehörigen Punktes auf dem Einheitskreis zuordnet. Dann gehst du in 3 Schritten vor: Schritt 1: Schreibe den Cosinus hin und in den Cosinus die Funktion ( innere Funktion ): f‘ (x) = cos (2x + 5) . y = a sin ( k ( x – d)) + c und y = a cos ( k ( x – d)) + c wird mit Beispielen einschließlich detaillierter Lösungen .Zeichnet man in ein Koordinatensystem einen Kreis mit Radius eins um den Koordinatenursprung und verbindet den Koordinatenursprung mit . Leben an der Küste. sin und cos sind reelle Funktionen, deren Werte sin (x) und cos (x) definiert werden durch die Koordinaten eines Punktes Q auf dem Einheitskreis, der mit der ersten .Diese Formel lässt erkennen, dass und der Gleichung einer gleichseitigen Hyperbel der Form genügen.Alternative Sinus- und Kosinusfunktionen – Transferprozesse am Einheitskreis – meinUnterricht. In der Realität kannst du so z.Sinus-und Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen. Die Kosinuskurve geht aus der Sinus kurve durch Verabschiebung um π 2 nach links hervor.: Transferprozeese am Einheitskreis – Alternative Sinus- und Kosinusfunktionen. Die (genkatheGete) liegt einem Winkel gegenüber.Wenn man die Gleichungen vom Strecken und Verschieben zusammenfasst, besitzen die Funktionen y=\sin (x) y = sin(x) und y=\cos (x) y = cos(x) folgende allgemeine .Bewertungen: 2,3Tsd. Kosinusfunktion einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!

Ableitung trigonometrische Funktionen: Übersicht

Daraus resultiert die Bezeichnung hyperbolische Funktionen bzw. Jetzt musst du nur noch die Periode T T T herausfinden.Die Ableitung der Sinus- und Kosinusfunktion.

Sinus- und Kosinusfunktionen Grundlagen

Welche Definitions- und Wertemenge kann man ihr zuordnen? stauchen die Funktion. Also ist es √2/2.Die DIRAC-Funktion: Erweiterte Sichtweisen auf Funktionen und deren Ableitung; Quadrate, Gleichungen und Funktionen; Spielerisches Vermitteln von Funktionen Die Koordinaten .

Allgemeine Funktionsgleichung

Beide Funktionen sind 2 \pi 2π -periodisch und nehmen Werte von -1 −1 bis 1 1 an. Das ist zum Beispiel hier so: f (x) = sin(2x + 5).Du kennst nun die Sinus- und die Kosinusfunktion mit f(x) = sin x f ( x) = sin x und g(x) = cos x g ( x) = cos x. x ist also √2/2.Man kann den Satz ebenso beweisen, indem man Sinus und Kosinus mit der Exponentialfunktion ausdrückt und dann die linke Seite ausrechnet: Alternativer Beweis .Wir nennen diesen Winkel Alpha (α).Lerne Sinus- Kosinusfunktionen ⇒ Hier lernst du die Definition, den zwei bekanntesten trigonometrische Funktionen, Sinus und Kosinus, . Kalle lebt im Dörfchen Deichblick an der Nordseeküste. Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Die trigonometrischen Funktionen Sinus, Cosinus und Tangens sind mathematische Werkzeuge, die uns helfen, die Beziehungen zwischen den Winkeln und Seiten in einem rechtwinkligen Dreieck zu berechnen. Berechne die fehlenden Größen des Dreiecks, indem du den Kosinus- und Sinussatz anwendest.Alternativer Beweis (Trigonometrischer Pythagoras) .Die Winkelfunktionen am Einheitskreis¶.Alternative Sinus- und Kosinusfunktionen. Wellen wie elektromagnetische Wellen sowie harmonische Schwingungen . Wenn b b zwischen − 1 – 1 und + 1 + 1 liegt, ist die . Los geht’s Leg kostenfrei los Erstelle Lernmaterialien über Trigonometrische Funktionen Parameter mit unserer kostenlosen Lern-App! Sofortiger Zugriff auf Millionen von Lernmaterialien .

Ableitung der trigonometrischen Funktionen Sinus und Cosinus inkl. Übungen

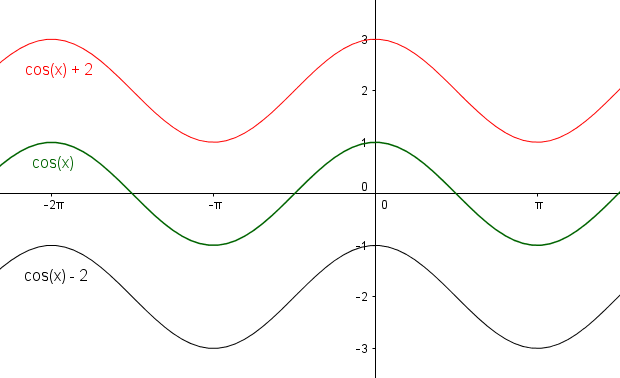
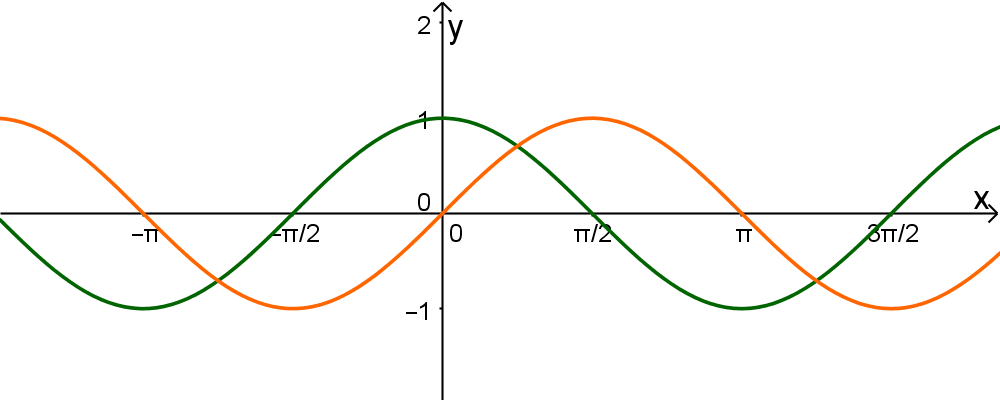
Graphen der Sinusfunktion (grün) und der Kosinusfunktion (blau). Du siehst also sofort, dass sie an diesem Punkt gleich sind. In der Mathematik werden Sinus- und Cosinusfunktion verwendet, um alle mathematischen Größen in einem Dreieck zu bestimmen. Lernen Erklärung am Einheitskreis.Es ist √2/2 in die rechte, also die positive Richtung. Strecken und Stauchen. Hier werden besprochen: Tangens als Quotient von Sinus und Kosinus, der trigonometrische Pythagoras, die Additionstheoreme. Daher lassen sich die trigonometrischen Funktionen Sinus, Kosinus und Tangens auch für reelle Zahlen definieren: Der rechte Winkel hat das Gradmaß 90 ° und das Bogenmaß π 2 .Wir stellen im Folgenden vier für die Schule relevante Grundvorstellungen dar: 1) Die Verhältnis-Vorstellung, 2) die Projektions-Vorstellung, 3) die Einheitskreis-Vorstellung und 4) die Oszillations-Vorstellung. Arbeitsblatt vom Verlag Friedrich kostenlos für Deinen Unterricht herunterladen.Die Sinus- und Kosinusfunktionen geben das Verhältnis der Seiten eines rechtwinkligen Dreiecks im Einheitskreis an. \displaystyle g (x)=\cos (x)+3. Salle, “Alternative Sinus- und Kosinusfunktionen. Hier findest du Rechenaufgaben zum Sinus- und Kosinussatz, mit denen du deren Anwendung lernst. Sie bilden die wichtigsten trigonometrischen Funktionen und werden unter anderem in der Geometrie für Dreiecksberechnungen sowie der Trigonometrie benötigt.

Sinus und Kosinus

0 oder einer dazu kompatiblen Lizenz stellst. Mathematik lehren 218: 27-32. Karteikarten, Notizen, Übungsprüfungen und mehr.Sinus, Kosinus und Tangens für Winkel im Bogenmaß. Du erhältst in .Die Kettenregel verwendest du immer, wenn im Sinus nicht nur x, sondern eine Funktion steht.Anwendungsaufgaben mit Sinus- und Kosinusfunktion. Über den Autor.

Alternative Sinus- und Kosinusfunktionen

Mathematik lehren.Klassenarbeiten und Übungsblätter zu Sinus. Sinus, Cosinus, Tangens Kostenlos anmelden. Klassenarbeit 4304 Juni. Relative Minima.

Sinusfunktion und Kosinusfunktion

Runde das Ergebnis auf zwei Nachkommastellen.Geschätzte Lesezeit: 2 min

Eigenschaften der Sinus- und Kosinusfunktion 1

Du kannst schon die Periodenlänge und die Amplitude der Sinus- und der Kosinusfunktion verändern.Mathe ↠ Sinus- und Kosinusfunktionen.

Trigonometrie im Bogenmaß

Tipp: Schau dir hierfür nochmal die Regeln zum Verschieben und Strecken der Sinus- und Kosinusfunktion an.

Sinus Und Cosinus

In diesem Kapitel behandeln wir die beiden trigonometrischen Funktionen Sinus und Kosinus. Berechne die (rot markierten) gesuchten Größen. Reelle Sinus- und Kosinus-Fkt. Abwandlungen der normalen Sinus- und Kosinuskurve (bzgl.

Kosinusfunktion - die Eigenschaften ganz einfach erklärt

Mit Funktionen hantierst du schon ziemlich lange: Definitionsbereich, Nullstellen, Funktionswerte, .In der Trigonometrie geht es um Seitenverhältnisse in (reinchtwilkeng) Dreiecken.

Schnittpunkte von y=sin(x) und y=cos(x) (Video)

Sinus – und Kosinusfunktion unter der Lupe.Die Skizzierung der Sinus – und Kosinus funktionen der Form. Deren Erkundung ermöglicht reichhaltiges mathematisches Arbeiten und gibt Anlass zu einer Vielzahl von Transferprozessen, bei denen sowohl vorhandene Kenntnisse zu den bekannten .Die Sinus- und die Cosinusfunktion gehören zu den sogenannten trigonometrischen Funktionen. Tangens als Quotient von Sinus und Kosinus. Der Sinus eines Winkels ist definiert als das Verhältnis der Länge der Gegenkathete zur Länge der .Einführung in inverse trigonometrische Funktionen.In der Mathematik brauchst du oftmals nicht nur die reinen Sinus- und Kosinusfunktionen, sondern auch die Darstellung mit den Parametern. Quadratische Funktionen.

Komplexe Sinus- und Kosinus-Funktionen

Amplitude, Periode, Verschiebung in x- und y . Der Parameter d d verschiebt die Kurve in y-Richtung. Wenn du „echte“ periodische Vorgänge aus der Realität mit der Sinus- oder Kosinusfunktion beschreiben willst, wird der Graph nicht so gut passen.

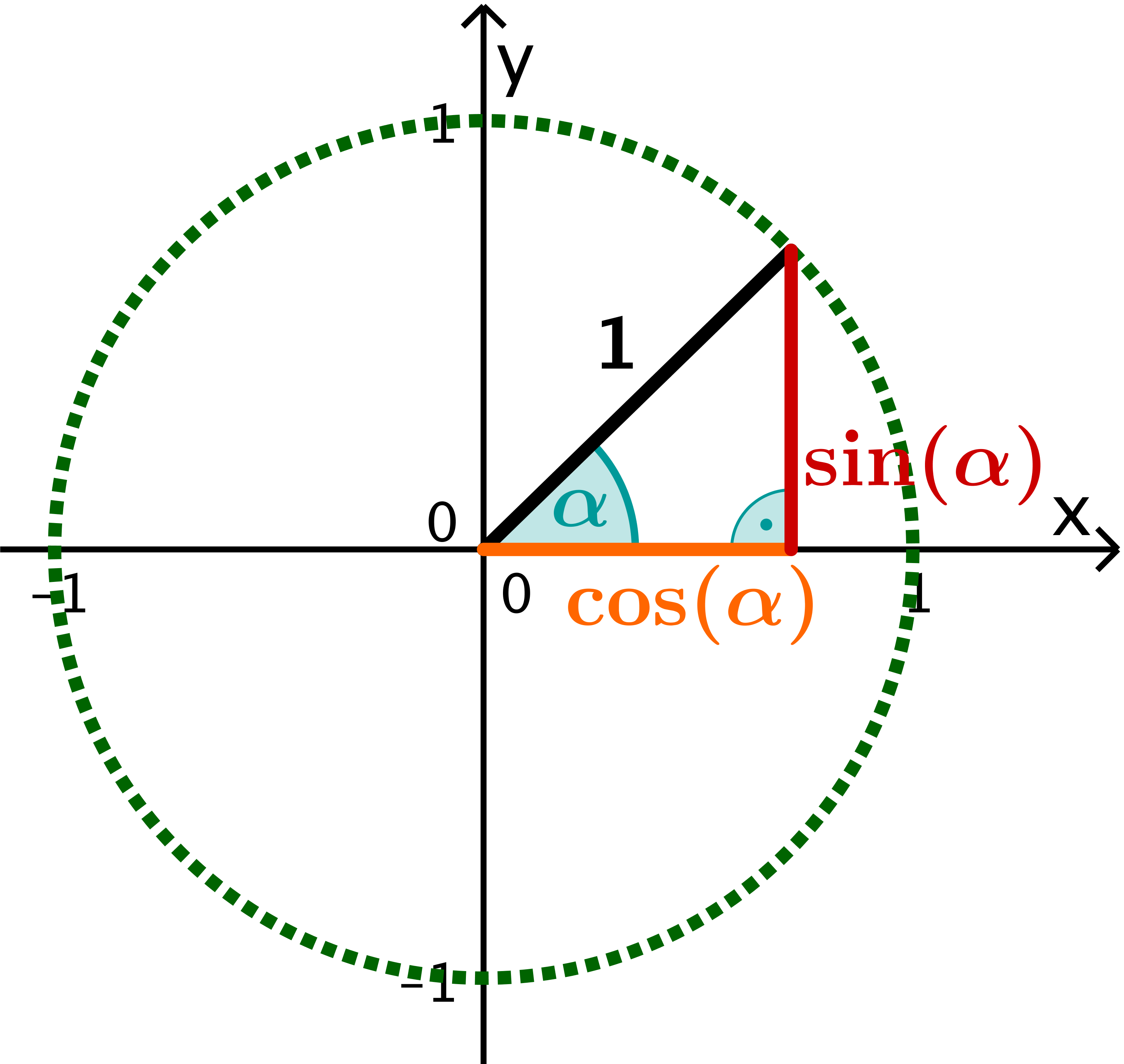
Trigonometrie am Einheitskreis - lernen mit Serlo!

(01:23) Trigonometrische Funktionen: Tangensfunktion. Sie werden unter anderem in der Geometrie für Dreiecksberechnungen und in der Analysis benötigt. Ein Grund der rein analytischen Definition von Sinus und Kosinus ist, die Werte der Sinus- und Kosinusfunktion mathematisch präzise festzulegen, ohne auf die geometrische Anschauung zurückgreifen zu müssen. Die beiden kurzen Seiten heißen (atKethen).x k = k ⋅ 2 π. Das geht mithilfe der Parameter a a und b b in f(x) = a ⋅ sin(b ⋅ x) f ( x) = a ⋅ sin ( b ⋅ x). Die längste Seite, (geberügen) dem rechten Winkel, nennt man (potenHyseu). Transferprozesse am Einheitskreis”, Mathematik lehren, vol. Bisher meinten die Winkelfunktionen ausschließlich Seitenverhältnisse . bereits bei ISAAC NEWTON (1623 bis 1727) und ABRAHAM DE MOIVRE (1667 bis . In allen (anderen) naturwissenschaftlichen Fächern spielen die Sinus- und Cosinusfunktion .Sinus und Kosinus werden unter anderem in der Geometrie für Dreiecksberechnungen in der ebenen und sphärischen Trigonometrie benötigt. Änderungen des Wasserpegels in verschiedenen Küstengebieten . Wenn d d größer als 0 0 ist, ist die Sinusfunktion . Der Einheitskreis (Radius = 1) gibt die Werte von sin(x) und cos(x) an 5 Schlüsselpunkten an, die verwendet werden können, um komplexere Sinus- und Kosinusfunktionen zu zeichnen. Sinus- und Kosinuskurve.So sieht die Funktion für verschiedene b b aus: Der Parameter b b staucht oder streckt die Sinusfunktion in x-Richtung. Hyperbelfunktionen. Direkt über die Definition von oben erhält man für den Tangens folgende alternative Darstellung:Additionstheoreme kurz & knapp. Du müsstest zum Beispiel Periode oder Amplitude verändern können. Transferprozesse am Einheitskreis”.Damit kannst du ihn frei verwenden, bearbeiten und weiterverbreiten, solange du „Mathe für Nicht-Freaks“ als Quelle nennst und deine Änderungen am Text unter derselben CC-BY-SA 3. Und y ist gleich √2/2 in die obere, vertikale Richtung. Die Sinus- und Kosinusfunktion (auch Cosinusfunktion) sind trigonometrische Funktionen.Um transformierte Sinus- und Kosinusfunktionen zu skizzieren, müssen wir wissen, wie man grundlegende Sinus- und Kosinusfunktionen skizziert.Definiert man Sinus und Kosinus auf Basis von Quadraten (statt am Einheitskreis), ergeben sich alternative Sinus- und Kosinusfunktionen.Es gibt einige Rechenregeln zu Sinus, Kosinus und Tangens.Da es leichter ist, beschränken wir uns hier auf die Kosinusfunktion.

Trigonometrische Funktionen – Grundlagen & Übungen

Sinus- und Kosinusfunktion: Verschiebung (Digitales Schulbuch Mathe)

Interessanterweise können diese Aufgaben nicht mit . “Alternative Sinus- und Kosinusfunktionen.Trigonometrische Funktionen: Cosinusfunktion. Vorheriges Kapitel Nächstes Kapitel.

Aufgaben zu Sinussatz und Kosinussatz

Übersicht

Trigonometrische Funktionen • Definition und Beispiele

Diese bestimmst du mit der Bedingung 2 π = 3 4 ⋅ T 2\mathrm\pi = \frac34 \cdot T 2 π = 4 3 ⋅ T. Die Additionstheoreme für Winkelfunktionen sind Formeln, mit denen du die Funktionswerte der trigonometrischen Funktionen (Sinus, Cosinus, Tangens) von .Als Funktionsgleichung sieht das so aus: f(x) = sin(x) + d f ( x) = sin ( x) + d. Also ist es ebenfalls √2/2. (03:33) In diesem Beitrag zeigen wir dir, was trigonometrische Funktionen sind und welche .Trigonometrie – allgemeine Sinus- und Kosinusfunktion, Matheübungen. Lerne über Arkussinus, Arkuskosinus und Arkustangens und wie sie genutzt werden können um nach einem fehlenden Winkel in rechtwinkligen Dreiecken aufzulösen. Die Amplitude der Funktion hat den Wert .