SIZZ

Wie die Ergebnisse der Würfelwürfe ist der Mittelwert vom Zufall abhängig.3 beinhaltet mit Binomialverteilung, . Genauer gesagt kann ein Zufallsexperiment zu n verschiedenen möglichen Ausgängen führen, nämlich zu allen . Eine formale mathematische Definition . Synonym hierfür wird auch oft der Begriff Zufallsgröße verwendet.

Mit den Zufallsvariablen wird uns ein wichtiges Instrument zur Seite stehen, um die Ergebnisse eines Zufallsexperiments zahlenmäßig zu erfassen. X: Ω → R; X: ω → X ( ω) = x. Die negative Binomialverteilung (auch Pascal-Verteilung) beschreibt die Wahrscheinlichkeit, dass eine . Diesen Wert nennt man Realisierung der Zufallsvariable, .Deine Zufallsvariable X ist gerade die Zuordnung der Farben zu den Farbnummern, sie kann also hier die Werte 1, 2 oder 3 annehmen.Wahrscheinlichkeitsrechnung – Definition. In diesem Kapitel lernen wir Zufallsvariablen als natürliches und suggestives . Die folgende Definition will zwei Sachverhalte ausdrücken: (i) . Sei beispielsweise Augensumme bei zweimaligem Würfeln Wir erwähnen .

Außerdem erklären wir, wie man die Wahrscheinlichkeit oder den Erwartungswert einer .1 Begriff der Zufallsvariable Im vorhergehenden Kapitel wurden den Elementarereignissen und anderen Ereig-nissen eines Zufallsexperimentes Wahrscheinlichkeiten zugeordnet. Entsprechende Begriffe und Eigenschaften für stetige Zufallsvariablen ergeben sich dann durch den Übergang vom diskreten zum stetigen Fall (Kap.

Erwartungswert

Eine Funktion X, die jedem Elementarereignis ω ∈ Ω genau eine reelle Zahl X(ω) ∈ zuordnet, wird als Zufallsvariableoder stochastische Variable bezeichnet.

Unendliche Teilbarkeit

Zufallsvariablen werden zur Beschreibung interessierender Aspekte bei einem zufälligen Vorgang verwendet.Sie ist das zentrale Moment zweiter Ordnung einer Zufallsvariablen.Eine Zufallsvariable oder Zufallsgröße ist eine Größe, die bei einem Zufallsexperiment nicht exakt vorhersagbare Werte annimmt.Der Erwartungswert (selten und doppeldeutig Mittelwert) ist ein Begriff der schließenden Statistik. Wenn Zufallsexperimente wiederholt unter gleichen Bedingungen und unabhängig voneinander durchgeführt werden, erhält man unabhängige Zufallsvariablen \(X_1,\dots ,X_n\) , die als Stichprobenvariablen . Eine Zufallsvariable bildet die möglichen Ergebnisse eines Zufallsexperiments ab, indem sie den Ergebnissen Zahlen zuordnet und durch die . der Stichprobenvarianz, bestimmt werden. Die Standardabweichung entspricht der Wurzel der Varianz und ist somit auch gleich Eins.Bei einer engeren Definition ist der Erwartungswert einer Zufallsvariablen eine reelle Zahl und damit endlich; bei einer weiteren Definition sind für den Erwartungswert einer .Eine Zufallsvariable ist eine Variable, deren numerischen Werte Ergebnisse von Zufallsexperimenten sind. Die Quadratwurzel der Varianz ist das als Standardabweichung bezeichnete wichtigste Streuungsmaß in der Stochastik .

Zufallsvariablen mit Dichte

Wir erw hnen jedoch schon jetzt ein wichtiges Unterscheidungsmerkmal: diskrete . Die Verteilung einer Zufallsvariablen ermöglicht es, . Bei der Be-trachtung eines Zufallsexperimentes treten nun aber häufig Situationen auf, die es erforderlich machen, den Elementarereignissen . Wir erwähnen jedoch schon jetzt ein wichtiges Unterscheidungsmerkmal: diskrete Zufallsvariablen haben einen abzählbaren Wertebereich, z. Einer ist der durchschnittliche . Werte der Zufallsvariablen werden entweder mit „ \ (X_ {i}\) “ oder mit „ \ (x\) “ bezeichnet.Eine Zufallsvariable oder Zufallsgröße ist ein Begriff aus dem mathematischen Teilgebiet Stochastik. Wenige aber wissen wohl, dass der Begriff des Zufalls in .Die Verteilung einer Zufallsvariablen ist ein Begriff aus der Wahrscheinlichkeitstheorie, einem Teilgebiet der Mathematik. Die Varianz kann mit einem Varianzschätzer, z. ihre Verteilung) hei t diskret, falls es eine abz hlbare Teilmenge gibt, so dass .Beim Würfeln mit zwei Würfeln ordnet die Zufallsvariable „Summe der Augenzahlen“ den Zahlenpaaren (1; 1), (1; 2), . Wenn das Experiment die Ergebnismenge . Zum Mathe-Abi Kurs.In der Stochastik ist eine Zufallsvariable eine Größe, deren Wert vom Zufall abhängig ist. Hat zum Beispiel eine Serie von zehn .

Mehrdimensionale Zufallsvariablen

Zufallsvariablen (auch Zufallsgrößen genannt) ordnen jedem Ergebnis eines Zufallsexperiments eine reelle Zahl zu. Meistens werden bei der Berechnung von Wahrscheinlichkeiten Zufallsexperimente betrachtet. Damit du mit Wahrscheinlichkeiten rechnen kannst, ist es wichtig, dass du einige Begriffe und Formeln kennst. Die Zufallsvariable (bzw.Der Begriff der absolutstetigen Zufallsvariablen wird später in Abschnitt 3.Standardisierung (Statistik) Unter Standardisierung oder z-Transformation versteht man in der mathematischen Statistik eine Transformation einer Zufallsvariablen, so dass die resultierende Zufallsvariable den Erwartungswert Null und die Varianz Eins besitzt.

Zufallsvariablen

Eine Funktion $X$, die jedem Ergebnis $\omega$ des Ergebnisraum $\Omega$ genau eine Zahl $x$ der Menge der reellen Zahlen $\mathbb{R}$ zuordnet, heißt Zufallsvariable.1 Das Konzept der Zufallsvariablen.Bei diskreten Zufallsvariablen hatten wir die gemeinsame Verteilung von mehreren Zufallsvariablen betrachtet, die insbesondere für zwei Zufallsvariablen in einer Tabelle dargestellt werden kann. Eine Variable X ist eine . Ist diese Größe eine reelle Zahl, so spricht man von einer reellen Zufallsvariablen oder Zufallsgröße.Zufallsvariable = Funktion, bildet Elementarereignisse eines Zufallsexperiments auf Werte ab.Besonders interessiert man sich bei einer Zufallsvariable für zwei Kennwerte, Parameter genannt, die die Zufallsvariable genauer beschreiben. Jedoch sind wir der Ansicht, dass er das Verständnis der Materie vereinfacht, daher werden wir diesen Begriff hier nutzen.

Wahrscheinlichkeitsrechnung

Zufallsvariable- Die Zufallsvariable heißt quasi-integrierbar, wenn der . Sie ordnet jedem Ergebnis eines Zufallsexperiments eine reelle Zahl zu: X: Ω → Zum Beispiel kann ein .Eine Zufallsvariable heißt integrierbar, wenn der Erwartungswert der Zufallsvariable existiert und endlich ist.Eine Einführung in die negative Binomialverteilung. Der Begriff der Unabhängigkeit sowie Kovarianz und Korrelation spielten dabei eine wichtige Rolle. Bei der Wahrscheinlichkeitsrechnung dreht sich alles um das Berechnen von Wahrscheinlichkeiten. Dies kann man dadurch modellieren, dass man eine Menge \ (\varOmega^\prime\) und eine Abbildung \ (X\,:\, \varOmega \rightarrow \varOmega^\prime\) wählt und X ( ω) anstelle des Ergebnisses ω des . Im Unterschied dazu ist der Erwartungswert eine feste Kennzahl der Verteilung der Zufallsvariablen . mit Namen ist so in Lehrbüchern nicht zu finden, da er gänzlich unmathematisch ist. Wird beispielsweise bei einer zufällig ausgewählten Person die . Oft interessieren nur Teilaspekte des Ergebnisses eines Zufallsexperimentes.Eine Zufallsgröße, oder auch Zufallsvariable, ist eine Funktion X.2 bei der Definition und Darstellung von Verteilungen, von Lage- und Streuungsparametern sowie Quantilen besonders deutlich. Der Erwartungswert ( \operatorname {E} (X) E(X) oder \mu μ) einer Zufallsvariablen (X) (X) ist jener Wert, der sich (in der Regel) bei oftmaligem Wiederholen des zugrunde liegenden Experiments als Mittelwert der Ergebnisse ergibt.In diesem Kapitel erweitern wir unsere bisherigen Kenntnisse der Wahrscheinlichkeitsrechnung um den Begriff der Zufallsvariablen. Zufallsvariablen. Im Video erfährst ganz entspannt alles, was du zu Verteilungen wissen musst.Im zweiten Schritt ist aus der Aufgabenstellung ersichtlich, dass die Träger der Zufallsvariablen $\Omega = \{0,1,2\}$ sind. Formal ist eine Zufallsvariable eine Funktion, die jedem möglichen Ergebnis eines Zufallsexperiments eine Größe zuordnet.Der Trainer beschäftigt sich mit der formalen Definition des Begriffs Zufallsvariable und erklärt auch, warum es sich dabei um einen eher irreführenden Begriff handelt. Die Bezeichnung Varianz wurde vor allem von dem britischen .14 definiert wurde.Erwartungswert, Varianz und Standardabweichung. Der Erwartungswert wird folgendermaßen berechnet: 1. Zufallsvariablen werden mit einem lateinischen Großbuchstaben, z. Schreibweise gewöhnlich: X(ω) = x (der dem Elementarereignisω zuzuordnende Wert ist x). Beachte Der Begriff der absolutstetigen Zufallsvariable wird später in Definition 3.1 Der Begriff der Zufallsvariablen. Der Begriff der absolutstetigen Zufallsvariablen . An dieser Stelle muss man sich die Frage stellen, was wirklich größer gleich Eins ist. Unabhängigkeit von Zufallsvariablen (stochastische Unabhängigkeit) Zufallsvariablen.Der Zufall ist uns vertraut, wir reden von den Zufälligkeiten des menschlichen Lebens, der Philosoph etwas vornehmer von der Kontingenz. Man bezeichnet damit eine Funktion, die den Ergebnissen eines .

Begriff der Zufallsvariable

Es gibt eine ganze Reihe von Vorgängen, die sich bei gleichbleibenden Bedingungen beliebig .3 Die Zufallsvariable (bzw.Skizziere die Dichtefunktion der Zufallsvariablen X, die in der Aufgabe 6.

Zufallsvariablen • Statologie

Der Ausdruck ohne Namen bzw.

Was sind Zufallsvariablen?

Der Begriff der Unabhängigkeit von Zufallsvariablen wird auch in den folgenden Kapiteln eine wichtige Rolle spielen.Wahrscheinlichkeitsverteilung. Übersetzt bedeutet das: Der Bereich, in dem der Funktionswert \ (f (x)\) (also der Wert auf der \ (y\)-Achse) größer als 0 ist. Man bestimmt die Wahrscheinlichkeitsverteilung der Zufallsvariablen. Wir wissen, dass vieles Mögliche und manches Unmögliche passieren kann, ohne dass wir eine Notwendigkeit dafür einsehen.Allgemein: Der Erwartungswert einer Zufallsvariablen gibt an, welcher Wert durchschnittlich bei einer großen Zahl von Durchführungen des Zufallsversuchs für die Zufallsvariable zu erwarten ist. Die einzelnen Ausprägungen bzw.Als Zufallsvariable bezeichnet man eine messbare Funktion von einem Wahrscheinlichkeitsraum in einen Messraum.Wir unterscheiden 2 (Grund-) Typen von Zufallsvariablen: diskrete und absolutstetige Zufallsvariable.von Zufallsvariablen. In unserem Fall also das Intervall von 0 bis 1 (strikt gesagt ohne der Null). Wir lernen die .Der Träger einer Zufallsvariablen ist einfach die Menge aller möglichen Ergebnisse von \ (X\). Üblicherweise schreibst Du die Zufallsvariable in Großbuchstaben, ihre Realisation zur Unterscheidung dagegen in .

Zufallsvariable

Zufallsgröße • Definition, Arten und Beispiele · [mit Video]

ihre Verteilung) heißt diskret, falls es eine abzählbare Teilmenge gibt, so daß .Der anschaulichen Vorstellung von einem Merkmal entspricht im mathematischen Modell für einen stochastischen Vorgang der Begriff einer Zufallsvariablen. Gib die Dichtefunktion jener Zufallsvariablen an, die auf dem Intervall [a, b] uniform verteilt ist.

Zufallsvariablen und Verteilungen

, (6; 6) eine der Zahlen zwischen 2 und 12 zu.

Man unterscheidet diskrete Zufallsvariablen , die nur ganz bestimmte Werte annehmen können (Anzahl der geschossenen Tore beim WM-Finale) und stetige Zufallsvariablen , die .

Der Begriff der absolutstetigen Zufallsvariable wird sp ter in Definition 3.Eine Zufallsvariable X ist eine Funktion, die jedem Ergebnis ω vom Ergebnisraum Ω eines Zufallsexperiments eine reelle Zahl x zuordnet. Zufallsvariablen und ihre Verteilungen, bedingte Wahrscheinlichkeiten, stochastische Unabhängigkeit, . Die Definition des Erwartungswerts steht in Analogie zum gewichteten Mittelwert von empirisch beobachteten Zahlen. Man kann den Begriff der Dichtefunktion losgelöst von Beispielen definieren.

Grundlagen der Inferenzstatistik 1: Zufallsvariablen

Zufallsvariablen

Wahrscheinlichkeitsverteilung · Anschauliche Erklärung

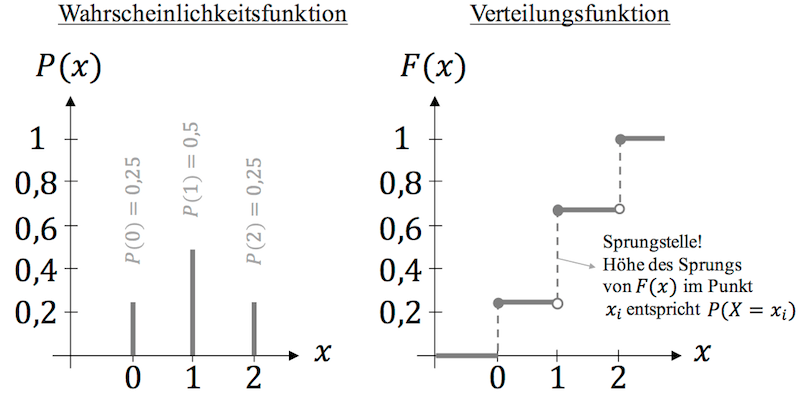
In diesem Artikel erklären wir dir, was eine Wahrscheinlichkeitsverteilung ist und wie du diskrete und stetige Zufallsvariablen mit der Dichtefunktion und der Verteilungsfunktion beschreiben kannst. „ \ (X\) “, symbolisiert.Der Erwartungswert ist eine Kennzahl einer Zufallsvariablen.

Beispiele für reelle . Eingeführt wurde der Begriff 1929 durch den italienisch-österreichischen Mathematiker Bruno .Der Erwartungswert (selten und doppeldeutig Mittelwert) ist ein Grundbegriff der Stochastik.Geschätzte Lesezeit: 2 min

Zufallsvariable

Der Begriff der unendlichen Teilbarkeit (auch als unbeschränkte oder unbegrenzte Teilbarkeit bezeichnet) beschreibt in der Stochastik die Eigenschaft vieler Zufallsvariablen, sich als Summe einzelner unabhängiger Zufallsvariablen zerlegen zu lassen. Mathe lernen mit abiturma: Alles zum Thema Zufallsvariablen aus dem Bereich Stochastik Wissenswertes, Tipps und Tricks sowie Aufgaben zur Stochastik. Zufallsvariablen werden in der Regel mit Großbuchstaben und ihre Realisierungen mit Kleinbuchstaben bezeichnet.wichtiger Begriff der Wahrscheinlichkeitstheorie.1 Diskrete Zufallsvariablen.Zufallsvariable Definition.Eine Zufallsvariable ordnet Ereignissen reelle Zahlenwerte zu. Dies kann auch für Zufallsvariablen mit .Vor dem Würfelwurf ist der Wert von \(X\) unbekannt, und nach dem Wurf nimmt \(X\) einen Wert von \(1, 2, 3, 4, 5, 6\) an. Tritt ein bestimmtes Ereignis ein, so sprichst Du von der Realisation x der Zufallsvariablen X.

Grundlegende Begriffe der Stochastik sind u. Wie hängen die Begriffe Wahrscheinlichkeitsverteilung und Zufallsvariable zusammen? Jedes Ergebnis eines Zufallsexperiments wird mit einer bestimmten .Dieser Artikel befasst sich mit Zufallsvariablen und behandelt Zufallsgrößen im diskreten und stetigen Fall.

• Reise in die champagne – champagne tourismus
• Durch schwere stürme mehr über das erdinnere erfahren – wie wird die erde gebildet
• Halloween-wunden schminken – wunden schminken hausmittel
• Week 10 lecture 26. sum of independent normal random variables: sum of random variables
• So zähmen chefs schwierige charaktere im berufsalltag – schwierige chefs charaktere
• Aktuelles zum ford nugget, matist xl und mehr | ford nugget neu