Berechenbarkeit hilberts vermutung loop-vermutung

(A+) Beweise von vielen Abschlußeigenschaften, daß die Klasse .

Riemannsche Vermutung

Heute wird als starke Goldbachvermutung gehandelt, dass alle geraden Zahlen größer als 2 Summe von zwei Primzahlen seien.Bewertungen: 67Argument (K ) gegen die Loop-Vermutung: Die Ackermann-Funktion 1.Berechenbarkeit Argument (K) gegen die Loop-Vermutung Behauptung Es gibt eine intuitiv berechenbare Funktion N ! N,dienicht loop-berechenbar (und damit auch nicht .: Eine Funktion f: IN k -> IN heißt LOOP-berechenbar, falls es ein LOOP-Programm gibt, das f berechnet, d.: Eine Turingmaschine ist ein 7-Tupel M = (Z, , , , z0 . Kreuzworträtsel Lösungen im ältesten deutschen Kreuzworträtsel-Lexikon.Collatz-Vermutung: Für jede beliebige Startzahl geht die durch die rekursive Bildungsvorschrift $a_1=s$ $a_{n+1}=\begin{cases} \displaystyle\frac{a_n}{2} & .LOOP-Programme sind Programme in der Programmiersprache LOOP, einer stark eingeschränkten, modellhaften Sprache, die nur die Formulierung von Additionen, Wertzuweisungen und endlich oft durchlaufende Schleifen erlaubt.Berechenbarkeit.Vermutung (Sprache: Deutsch) Wortart: Substantiv, weiblich Bedeutung/Definition eine ungesicherte Erkenntnis oder Annahme Artikel/Genus Das grammatikalische Geschlecht ist feminin, es heißt also die Vermutung.Auf den deutschen Mathematiker Lothar Collatz (1910 – 1990) geht die (3n+1)-Vermutung zurück (siehe Seite Das Collatz-Problem).Berechenbarkeit Ein bißchen Geschichte (vgl. Teil der heutigen Vorlesung: Wilhelm Ackermann (1886-1962) konstruierte 1928 eine Funktion, die intuitiv berechenbar ist, und bewies, daß sie nicht primitiv-rekursiv (d. P gestartet mit der Variablenbelegung n1, .

Hilbertsche Probleme

Wir sehen uns LOOP-Programme als ein Berechnungsmodell ähnlich den WHILE-Programmen an.Vermutung und Fiktion.Berechenbarkeit und Komplexität Vorlesung SS 2013 1., nk der Variablen . Umgekehrt kann die Loop-Vermutung nur gestützt werden, wie z.

Primzahlen und Riemann-Vermutung bei 3sat – Mathlog

Mit anderen Worten: (K+) Beweise von vielen Funktionen, daß sie loop-berechenbar sind. Rósza Péter . (§ 985) Wenn der eine Eigentümer und der andere .SS 23 Berechenbarkeit und Komplexität 1.

Hilberts Vermutung ) Loop-Vermutung

Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 13. Berechenbarkeit.Turing-Berechenbarkeit.Das Hilbert´sche Programm: Ziel ist es, die Mathematik so zu formalisieren, dass die folgenden Bedingungen erfüllt sind: Widerspruchsfreiheit: Die Formalisierung soll . LOOP-Programme sind weniger mächtig als WHILE-Programme, allerdings l. Einleitung (Berechenbarkeitsmodelle) Die hier behandelten Berechenbarkeits-Ansätze dienen als Hilfsmittel zum Beweis, ob bestimmte Probleme berechnet werden können, .Turing-Berechenbarkeit X 13. (partielle) Überführungsfunktion z0 Anfangszustand.Sommersemester berechenbarkeit hilberts vermutung lemma jede primitiv rekursive funktion nr ist beweis: durch induktion über den aufbau von zeigen wir, daß ist

VL-10: LOOP und WHILE Programme II

Kurt Gödel, der ebenso wie Hilbert an der Frage interessiert war, was ein Verfahren sei, kannte keine While-Programme, sondern formulierte die folgende Vermutung: Gödels .

Zur Riemannschen Vermutung und ihrer Geschichte – Mathlog

Die Vorstellungswelt des Gesetzgebers ist einfach: Tatbestand und Rechtsfolge werden einfach verknüpft – wenn etwas bestimmtes gegeben ist, dann tritt eine bestimmte Rechtsfolge ein.

Zur Riemannschen Vermutung und ihrer Geschichte.Hilberts Vermutung (1926) Eine Funktion N k N mit k C 0 ist genau dann intuitiv berechenbar, wenn sie primitiv-rekursiv ist.In diesem Video zeige ich euch, wie man Berechenbarkeit mithilfe der LOOP Programmiersprache zeigen kann und wie man aus der minimalistischen Syntax beispiel.Es gibt mathematische Probleme, die sich algorithmisch gar nicht lösen lassen. 1934) Eine partielle Funktion Nk 99K N ist genau dann intuitiv berechenbar, wenn sie µ . Für ungerade Zahlen ist diese Aussage offensichtlich falsch: Wenn zwei Primzahlen in der Summe eine ungerade Zahl ergeben sollen, dann muss genau eine der beiden Primzahlen gerade sein, was nur auf .primitive Rekursion und -Rekursion 15. physikalische Gesetze gestützt werden: Versuche, die Loop-Vermutung zu widerlegen, und scheitere dabei.

Fehlen:

Berechenbarkeit

LOOP Berechenbarkeit - YouTube

Ackermannfunktion 16.LOOP-berechenbare Funktionen 00:18:25: Die Turmfunktion 00:23:40: Laufzeit von LOOP-Programmen 00:25:08: Vermutung von Hilbert 00:26:34: Ackermann: Vermutung ist .LOOP-berechenbare Funktionen 00:18:25: Die Turmfunktion 00:23:40: Laufzeit von LOOP-Programmen 00:25:08: Vermutung von Hilbert 00:26:34: Ackermann: Vermutung ist falsch! 00:28:33: Die Ackermann-Funktion 00:37:47: Wachstum für feste m 00:40:49: Monotonieeigenschaften der Ackermannfunktion 00:51:14: Wachstum der .

David Hilbert: Die Theorie der algebraischen Zahlkörper

Damit waren die Loop- und die Hilbertsche Vermutung zu verwerfen.Postsches Korrespondenzproblem Unentscheidbare Grammatik-Probleme G odelscher Satz und diophantische Gleichungen.

Vermutungen: Aufräumen unter den Primzahlen

In dieser allgemeinen Form, ob es stetige Funktionen in drei Variablen gibt, die nicht als Verkettung von endlich vielen stetigen Funktionen in zwei Variablen dargestellt werden . Eine der Standardpräzisierungen des Berechenbarkeitsbegriffs verwendet Turing Maschinen (TMs).Später wurde sie verschärft: Die starke Goldbachsche Vermutung besagt, dass jede gerade Zahl größer als zwei sich als Summe aus zwei Primzahlen darstellen . loop-berechenbar) ist. Berechenbarkeitsbegriff, typische Fragen: wann ist eine Funktion berechenbar? wie lässt . Wir werden zeigen, daÿ Hilberts Vermutung .M achtigkeit von LOOP Vermutung von David Hilbert (1926) Die Menge der LOOP-berechenbaren Funktionen Nk!N stimmt mit der Menge der berechenbaren totalen .In Legendres Version geht es dort um quadratische Restsymbole \ ( (\frac {a} {p})\) für ungerade Primzahlen \ (p\) und zu \ (p\) teilerfremden Zahlen \ (a\), deren Werte \ (\pm1\) .

Riemannsche Vermutung, Zahlentheorie #44 - YouTube

Sind k ≥ 1, g ∶ Nk−1→ N und h∶ Nk+1→ N loop-berechenbar, so auch die Funktion rec(g , h)∶ Nk→ N.Turing-Berechenbarkeit 13. Weltweit versuchen sich immer wieder etliche Personen an einem Beweis, doch bisher .22) Alonzo Church und Alan Turing, die ebenso wie Hilbert und Gödel an der Frage interessiert waren, was ein „Verfahren“ sei, kannten keine While- oder Goto-Programme, sondern formulierten die folgende Vermutung: Church-Turing-These (1936)

Zahlen, bitte! Hilberts noch immer nicht gelöstes achtes Problem

Seit über 160 Jahren zählt die riemannsche Vermutung zu einem der härtesten Problemen der Mathematik.Alle Fälle (Nominativ, Genitiv, Dativ, Akkusativ) im Singular und Plural sind unter dem Punkt Grammatik/Fälle aufgeführt. Der Eigentümer kann vom Besitzer die Herausgabe der Sache verlangen.Kurt Gödel, der ebenso wie Hilbert an der Frage interessiert war, was ein „Verfahren“ sei, kannte keine While-Programme, sondern formulierte die folgende Vermutung: Gödels . LOOP-Programme spielen in der Theoretischen Informatik eine Rolle, insbesondere im Zusammenhang mit .VERMUTUNG 44 Lösungen zum Kreuzworträtsel ️ Die Lösungen aus dem Lexikon sind 5 bis 20 Buchstaben lang.Postsches Korrespondenzproblem Unentscheidbare Grammatik-Probleme G odelscher Satz und diophantische Gleichungen M.Berechenbarkeit Umgekehrt kann die Loop-Vermutung nur gestützt werden, wie z.

Syntaktische Komponenten für While-Programme

Berechenbarkeit #17

13) Kurt Gödel, der ebenso wie Hilbert an der Frage interessiert war, was ein „Verfahren“ sei, kannte keine While-Programme, sondern formulierte die folgende Vermutung: Gödels Vermutung (ca.Das Hilbertprogramm ist ein Forschungsprogramm, das der Mathematiker David Hilbert in den 1920er Jahren vorschlug. Genauer: Die Differenz skaliert höchstens mit der Wurzel von n (√ n ); . Es gibt bekanntlich die sieben Milleniumprobleme, auf deren Lösung das Clay Mathematical Institute zu Beginn des Jahrtausends jeweils eine Million Dollar ausgesetzt hatte und von denen bisher nur eines – die Poincaré-Vermutung – gelöst ist. Berechnungen Wiederholung: . 2 Turing-mächtige Programmiersprachen Definition Eine Programmiersprache wird als Turing-mächtig bezeichnet, wenn jede Funktion, die durch .Entscheidbarkeit, Reduktionen, Halteproblem 17.

Collatz-Problem

Solche unentscheidbaren Probleme zeigen uns die Grenzen der Berechenbarkeit auf.

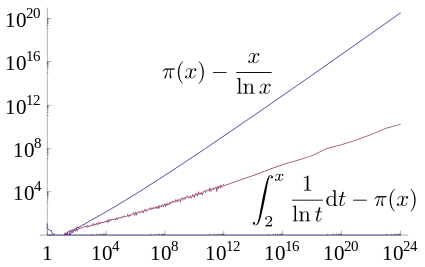
Riemannsche Vermutung – FunFacts Wiki

Die riemannsche Vermutung besagt, dass diese Abweichung nicht beliebig groß werden kann. Dazu gehören insbesondere das Halteproblem für Turingmaschinen, das Wortproblem und das Problem der Lösbarkeit ganzzahliger diophantischer Gleichungen. Teil der heutigen Vorlesung: Wilhelm Ackermann (1886-1962) konstruierte 1928 eine Funktion, die intuitiv berechenbar ist, und bewies, daÿ sie nicht primitiv-rekursiv (d.LOOP-, WHILE- und GOTO-Berechenbarkeit 14. Als kleine Spielerei können mit dem . endliche Zustandsmenge Eingabealphabet Arbeitsalphabet. Beweis: Die Funktion rec(g , h) läßt sich durch das .

Berechenbarkeit und Komplexität

Der Jungen Akademie und der Deutschen .1 Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP Programme Prof.

Grenzen der Berechenbarkeit » Ein Blick in die Geschichte

Es zielt darauf ab, mit finiten Methoden die . (Wiederholung): Def.