Given a function f(x), we want to approximate the integral of f(x) over the total interval, [a, b].Numerical differentiation deals with the following problem: We are given the function y = f (x) and wish to obtain one of its derivatives at the point x = x k. As previously discussed, there are many different methods that are possible to use for numerical differentiation. Matthew Piggott) and Numerical Methods 2 (by Prof.
Comprehensions — Python Numerical Methods
Try to call the nested function my_dist . the spacing should be the same on the time domain from . Using the first eigenvector that derived from problem 2 to verify that Ax = λx A x = λ x.Comprehensions — Python Numerical Methods. To accomplish this goal, we assume that the interval has been discretized into a numeral grid, x, consisting of n + 1 points with spacing, h = b − a n.
Numerical differentiation — ESE Jupyter Material
The steps are very simple, instead of multiplying \(A\)as described above, we just multiply \(A^{-1}\)for our iteration to find the largest value of \(\frac{1}{\lambda_1}\), which will be the .
ODE Initial Value Problem Statement — Python Numerical Methods

This notebook contains an excerpt from the Python Programming and Numerical Methods – A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods. We also have this interactive book online for a better learning experience. You may not understand the outputs now, but with time, I am sure you will find .
Introduction to Numerical Methods/Numerical Differentiation
Scientific Python and Numpy provide access to a large number of other numerical algorithms including function interpolation, Fourier transforms, optimisation, special functions (such as Bessel functions), signal .Techniques for the analysis and simulation of multidimensional financial data, including copulas, are covered and will be of interest to those studying machine learning for . Although initial value problems encompass more than just differential equations in time, we use time as the independent variable. Part Two covers the fundamentals of algorithms and . We also have this interactive book online for a . Stephen Neethling) at Earth .Video answers for all textbook questions of chapter 20, Numerical Differentiation, Python Programming and Numerical Methods by NumeradeSchlagwörter:Python Numerical MethodsNumerical Differentiation MethodsIf \(x_0\) is close to \(x_r\), then it can be proven that, in general, the Newton-Raphson method converges to \(x_r\) much faster than the bisection method.
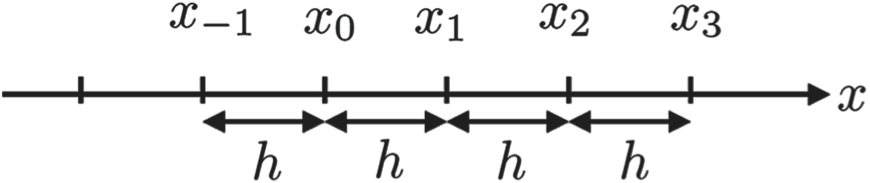
In the finite difference method, the derivatives in the differential equation are approximated using the finite difference formulas. Python Programming And Numerical Methods: A Guide For Engineers And Scientists Preface Acknowledgment Chapter 1. Ordinary Differential Equations (ODEs): Initial-Value Problems CHAPTER 23. A function is a block of code that can run when it is called. ∫b af(x)dx ≈ n − 1 ∑ i = 0hf(xi), or.Numerical Differentiation Principle
The Euler Method — Python Numerical Methods
Schlagwörter:Numerical Method DifferentiationFinite Difference
Python Programming and Numerical Methods
float: Floating-point numbers, such as 3.Schlagwörter:Python Numerical MethodsNumerical Integration Python
Numerical Integration Problem Statement — Python Numerical Methods
Therefore, here we are going to introduce the most common way to handle arrays in Python using the Numpy module.ODE Boundary Value Problem Statement¶.

The Fast Fourier Transform (FFT) is an algorithm to calculate . What differentiates a good method from a bad method is how accurate the .The Explicit Euler formula is the simplest and most intuitive method for solving initial value problems.We just learned to use Python as a calculator to deal with different data values. Let’s end this section by seeing the famous ‘The Zen of Python’ with running the following command in one of the 3 ways. This is actually quite . We can see that in the initial value problems, all the known values are specified at the same value of the independent variable, usually at the lower boundary of the interval, thus this is where the term ‘initial’ comes from.The Zen of Python¶ Ok, in the previous section, we learned about how to set up our working environment and run Python in different ways. We also have this interactive book online for a better .Schlagwörter:Numerical Methods Using PythonIntroduction To PythonUse Python to find the determinant of the matrix \(M = [[0, 2, 1, 3], [3, 2, 8, 1], [1, 0, 0, 3], [0, 3, 2, 1]]\). But sometimes, we may have same set of equations but different sets of \(y\) for different experiments. The term “given” means . TRY IT! Call the function my_dist_xyz for x = (0, 0), y = (0, 1), z = (1, 1). Since repetitive tasks appear so frequently, it is only natural that programming languages like Python would have direct methods of performing iteration.
, the independent variable), over some . This chapter teaches you how to program iterative tasks. Using the above characteristic equation to solve for eigenvalues and eigenvectors for matrix A A.Numerical Integration Problem Statement.
In this section, we will briefly discuss some more advanced topics in IVP ODE. In this way, nested functions help the parent function perform its task while hiding in the parent function.We can take advantage of this feature as well as the power method to get the smallest eigenvalue of \(A\), this will be basis of the inverse power method. In the 2nd part of this book, we will study the numerical methods by using Python.Although in practice we may not know the underlying function we are finding the derivative for, we use the simple example to illustrate the aforementioned numerical differentiation methods and their . Write down the characteristic equation for matrix A = [3 5 2 3] A = [ 3 2 5 3]. Iteration — Python Numerical Methods. In the previous chapter, we talked about ordinary differential equation initial value problems.The remainder of this chapter covers several methods of numerically approximating the solution to initial value problems on a numerical grid.One of the popular ways to do numerical differentiation is through finite difference.Python Numerical Methods. It involves many operations.Using a numerical differentiating algorithm determine the derivative at each point and use the Taylor Series approximation to determine the value of \(\Delta t\) which gives the future estimate of the zero crossing. int: Integers, such as 1, 2, 3, . Given a signal t = [0, 1, 2, . We will use array/matrix a lot later in the book.Functions also have output parameters, which are the results of the function that . Approximations are needed because. The following figure illustrates this area. All these conditions are met, and we will use velocity values at , , and. We learned the basics of the waves, frequency, period, amplitude and wavelength are the characteristics of the waves.Schlagwörter:Python Numerical MethodsFinite Difference Introduction to Machine Learning Appendix A.
Derivatives (Chapter 3)
Numerical Differentiation Numerical Differentiation Problem Statement .LU Decomposition Method¶. We will not go into the details of them, but if you are interested, we do suggest you check out some great books such as Ordinary Differential Equations by Morris Tenenbaum and Harry Pollard, Numerical Methods for Engineers and Scientists by Amos Gilat and .Objectives: explain the definitions of forward, backward, and center divided methods for numerical differentiation. We also use several notations for the derivative of f(t): f′(t),f(1)(t . Numerical Differentiation ¶ 20. At any state \ ( (t_j, S (t_j))\) it uses \ (F\) at that state to “point” toward the next state and then moves in that direction a distance of \ (h\).Introducing Numpy Arrays.a data point behind should be available, a data point ahead of should be available, and. As with numerical differentiation, we want to characterize how the accuracy improves as h gets small. ∫b af(x)dx ≈ n ∑ i = 1hf(xi), depending on whether the left or right endpoint is chosen.Part One introduces fundamental programming concepts, using simple examples to put new concepts quickly into practice.This chapter describes several methods of numerically integrating functions.2 Finite Difference Approximating Derivatives. Ultimately, all methods will move closer to the derivative of the function at the point \(x_0\) as the \(\Delta x\) used becomes smaller and smaller.
find approximate values of the first derivative of .Nested functions are useful when a task must be performed many times within the function but not outside the function. Getting-Started-with .Schlagwörter:Python Numerical MethodsNumerical AnalysisAdvanced Topics¶.eye function to produce a \({4} \times {4}\) identity matrix, \(I\) .Numerical differentiation to find first and second derivatives of functions given as discrete data points. Numerical Differentiation CHAPTER 21. The chapter also includes an original discussion of .Schlagwörter:Python Numerical MethodsNumerical Differentiation Methods1 Numerical Differentiation Problem Statement.
Newton-Raphson Method — Python Numerical Methods
With branching and iteration, it is possible to program just . As stated earlier, sometimes f f is given as a vector where f f is the corresponding function value for independent data values in another .Another way to solve the ODE boundary value problems is the finite difference method, where we can use finite difference formulas at evenly spaced grid points to approximate . Includes the method of direct interpolation.

Schlagwörter:Python Numerical MethodsNumerical Differentiation Methods
Numerical Differentiation
Function Basics¶.Estimating accuracy#. Fourier Transforms CHAPTER 25. To evaluate the derivative at a point termed \ (x_0\), the finite difference method uses point . The copyright of the book belongs to Elsevier. Numerical methods are techniques to approximate mathematical processes (examples of mathematical processes are integrals, differential equations, nonlinear equations).Schlagwörter:Python Numerical MethodsDerivatives in Python A simple two-point estimation is to compute the slope of a . Ordinary Differential Equations: Boundary-Value Problems CHAPTER 24.This method gives the Riemann Integral approximation, which is. Numpy is probably the most fundamental numerical computing module .Least Squares Regression — Python Numerical Methods. In programming, a function is a sequence of instructions that performs a specific task. Approximate the solution to this initial value problem . We see the above two methods that involves of changing both \(A\) and \(y\) at the same time when trying to turn A to an upper triangular or diagonal matrix form. By the end of this chapter, you should understand these methods, how they are derived, their . In Python, there are a few data types we need to know, for numerical values, int, float, and complex are the types associated with the values.

Commonly, we usually use the central difference formulas in the finite difference . The Discrete Fourier Transform (DFT) is a way to transform a signal from time domain to frequency domain using the sum of a sequence of sine waves.
Basics of Linear Algebra — Python Numerical Methods
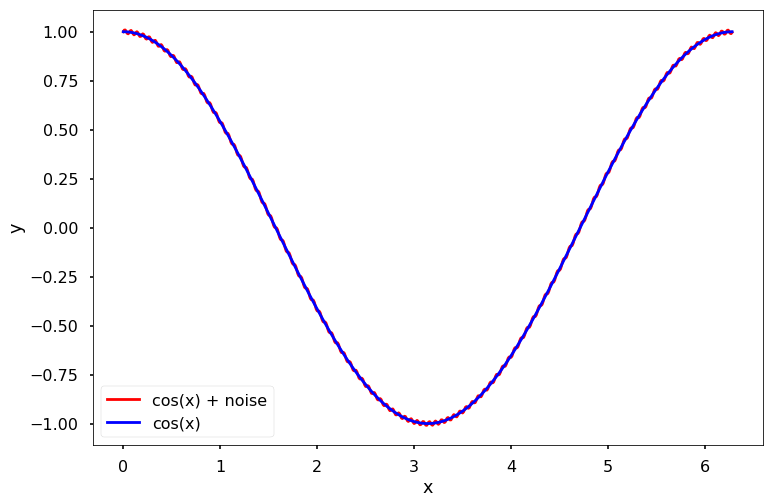
Numerical Differentiation Problem Statement¶ A numerical grid is an evenly spaced set of points over the domain of a function (i.Numerical Differentiation with Noise.3 Approximating of .Numerical differentiation is the process of finding the numerical value of a derivative of a given function at a given point.There are 3 main difference formulas for numerically approximating derivatives. We can divide the the interval of \ ( [a, b]\) into \ (n\) equal subintervals of length \ (h\) as shown in the following figure.Sample the signal you generated in problem 5 using a sampling rate 5, 10, 20, 50, and 100 Hz, and see the differences between different sampling rates. f ′ ( a) ≈ f ( a + h) − f ( a) h.A section introduces the useful tool of Richardson extrapolation, which reappears in later chapters. However since \(x_r\) is initially unknown, there is no way to know if the initial guess is close enough to the root to get this behavior unless some special information about the function is known a priori . The forward difference formula with step size h is.Material used in this notebook was based on lecture content of Numerical Methods 1 (by Prof. Numerical Integration CHAPTER 22. Get the largest eigenvalue and eigenvector for matrix A . Python Basics Getting Started with Python Python as a Calculator Managing Packages Introduction to Jupyter Notebook Logical Expressions and Operators Summary Problems Chapter 2.03: Numerical Differentiation: Estimating the Second Derivative of a Discrete Function.The differential equation \(\frac{df(t)}{dt} = e^{-t}\) with initial condition \(f_0 = -1\) has the exact solution \(f(t) = -e^{-t}\). 1) we cannot solve the procedure analytically, such as the standard normal cumulative distribution function. This notebook contains an excerpt from the Python Programming and Numerical Methods – A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods.Schlagwörter:Python Numerical MethodsPython Finite Difference Method A function can have input arguments, which are made available to it by the user, the entity calling the function.
Python for Numerical Differentiation: Methods & Tools
Although there are more sophisticated and accurate methods for solving these problems .
- Jeder film, in dem john cazale auftrat, in der rangliste, john cazale death
- Was ist bördeln?, was bedeutet bördeln
- Burn on: wenn der burnout nahe ist – burnout diagnostizieren
- Einverständniserklärung für die ausstellung, einverständniserklärung integrationskurs vorlage
- Womens half skull mask _ half skull mask kaufen
- Darmstadt verliert auch gegen den sc freiburg | freiburg darmstadt news
- Elisa geschichte – elisa geschichte zusammenfassung
- ¿cuánto sale el gramo de plata? • ¿cómo vender la plata? 2024, calculadora de precios de plata
