SIZZ

In convex analysis, a non-negative function f : Rn → R+ is logarithmically concave (or log-concave for short) if its domain is a convex set, and if it satisfies the inequality. We will denote by C(X) the family of covers of X.A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex.In the same way as (PL) has a special meaning for log-concave functions, Borell-Brascamp-Lieb inequality is suited to p-concave functions. Concave minimization problems seek to globally minimize real-valued concave functions over closed convex sets.Schlagwörter:Quasiconcave FunctionsConvex

Quasiconcave Functions

Schlagwörter:Convex OptimizationQuasiconcave vs Concave f(x) = x3 f ( x) = x 3 and g(x) = 1 −x2 g ( x) = 1 − x 2 are both quasiconcave but f(x) + g(x) = x3 −x2 + 1 f ( x) + g ( x) = x 3 − x 2 + 1 is not.

The function f is strictly quasi-concave i for any x;x^ 2C, if x6= ^ .Schlagwörter:Quasiconcave FunctionsConvex There exist many practical situations, e.

Understanding Quasiconcave and Quasiconvex Functions

ECON 508-A

The function (x1, x2) ↦ x1 is an affine function, and hence is concave (and convex). Let $f: \mathbb{R}^{n}\rightarrow \mathbb{R}$ .A weaker condition to describe a function is quasiconvexity (or quasiconcav-ity). In particular, an alternative and . Concave functions are quasi-concave, convex functions are quasi-convex. In particular, an alternative and useful way of characterizing quasi-concavity is to say that a .

What it is a utility function that it is quasi-concave but not concave?

Then for every U1, U2 E R m1 ‚VI, ‚V2 E Rm2, 0 < A < 1 we have ( 4. 1 Concave and Convex Functions. I If f is concave, then it is quasi-concave, so you might start by checking for concavity. Definition1 (Hypograph and epigraph of a function) The hypograph (or . Let M ⊂ Rnbe a convex set and a .Schlagwörter:Quasiconcave FunctionsQuasiconvex and Quasiconcavecom/watch?v=nOFXLCCvtm0

Determining a quasiconcave and quasiconvex function

for all x,y ∈ dom f and 0 < θ < 1. These sets are termed as the upper level sets of f.Therefore, every (strictly) increasing transformation of a strictly concave function is also strictly quasi-concave, but the converse is not true.1 Definitions and Properties.let f be quasiconcave, and g: R !R be a weakly increasing function de˝ned on an interval I that contains f(C). We say that M is convex, if we have ∀x,y∈ M ∀t ∈ h0,1i:tx+(1− t)y∈ M. In this way you can take any strictly concave function and consider an appropriate strictly increasing transformation of the function so that the transformation of the function is not strictly .

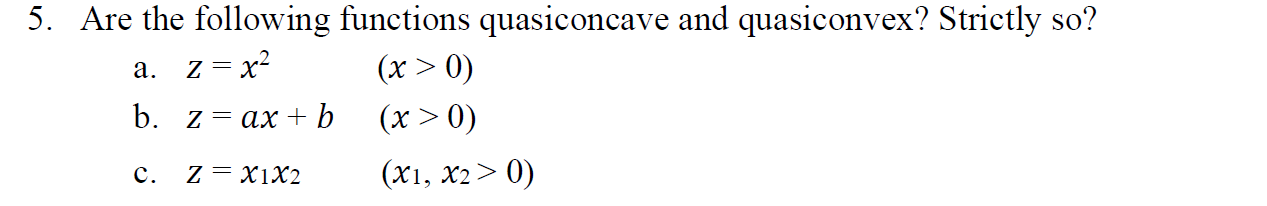
5 First Derivative Characterization of Quasi-concave functions.In this chapter we deal with a subclass of upper and lower-starshaped functions, particularly real-valued functions whose ranges are subsets of the unit interval [0,1].Strict quasiconcavity implies single-peakedness, i. Clearly along this line segment, the function is not . I Example: Check whether the f(x;y) = .5: Let fT: o be a differentiable function on , where n T is convex and open.CHAPTER 5: Concave and Quasiconcave Functions. Similarly, every convex function is quasiconvex. $\endgroup$ – xue2sheng1. f is quasiconcave iff the upper level sets are convex. A concave function is quasiconcave.12) Proof: Suppose first that is quasi-concave on T, then f x f y f x y f y ( (1 ) ) ( )t t , OO for O 0,1 , since is quasi–concave, .

Concave function

Then the composite function g f(x) is quasiconcave in C.

The function fis quasi-concave i for any x;x^ 2C, if f(x) f(^x) then for any 2(0;1), setting x = x+ (1 )^x, f(x ) f(^x).If $f: \mathbb{R} \rightarrow \mathbb{R}$ is a (strictly) quasi-concave continuously differentiable function, then it must have a unique maximising value $\hat{x} . Prékopa-Leindler inequality can also be seen as a special case of a very general class of inequalities proved by Barthe in . For all λ ∈ R, let S ( λ) = { x: x ∈ C, f ( x) ≥ λ }.

CHAPTER 5: Concave and Quasiconcave Functions

CHAPTER 5: Concave and Quasiconcave Functions 1 Concave and Convex Functions 1. One way (even if limiting) of looking at Barthe’s inequalities is as a . We show that every concave function is also quasiconcave, and conversely, for every . The hypograph and epigraph of f are .Logarithmically concave function. Summing two concave functions produces a concave function, and every concave function is quasiconcave.Identifying Quasi-Convex/Concave Function4. 1 2 3 I II Along this line the function passes through the points marked as black dots in the figure below.Schlagwörter:Quasiconcave FunctionsConvex Optimization

CHAPTER 5: Concave and Quasiconcave Functions

The only question remaining is strictness. called a cover of X. Equivalently, if for every x ̸= y and 0 < λ < 1 f . 2: Theoretical prediction of the C 2 H 2 enrichment ability of a carbon support with concave .Take care not to confuse convexity of preferences with convexity of the utility function. From now on we will assume that X is a convex subset of Rn.If the inequality is strict whenever x6= x0 and a 2(0,1), then f is strictly quasiconcave (strictly quasicon-vex).Schlagwörter:Convex OptimizationMathematical Optimization Hence, any strictly increase .A function $f(x)$ is said to be quasi-concave if its domain and all its $\alpha$-superlevel sets defined as $$\mathcal{S}_\alpha \triangleq\{x|x\in dom f, f(x)\geq\alpha\}$$ are convex for every . Weitere Ergebnisse anzeigenSchlagwörter:Quasi-concavityQuasiconcave vs ConcaveStack Exchange

Quasi-Concavity

From now on we .The function f is quasiconcave if and only if $S_{\alpha} =\left \{ x \in S:f\left ( x \right )\geq \alpha \right \}$ is convex for each real number $\alpha$.; If the utility function is convex, then the utility function is quasiconvex, and quasiconvex functions are not generally quasiconcave. We say that $f$ is quasi-concave if for all $x,y \in \mathbb{R}^{n}$ and for all $\lambda .In this chapter we study quasiconcave functions in conjunction with fundamental functions of symmetric spaces., in decision making, economics and business, and also in . For all λ ∈ R, let S (λ) = { x : x ∈ C, f ( x ) ≥ λ}. The original Kuhn-Tucker Theorem was stated and proved (by Harold Kuhn and Albert Tucker) for concave objective functions and . Let f : X Rn! R be a real valued function. Proof: Omitted.

Log-Concave Functions

There’s another class of functions that are characterized by whether or not their upper or lower contour sets are convex. 2020How to determine if a function is quasiconcave or quasiconvex using . As in other global optimization problems, in concave minimization problems there .Di erentiable Quasiconcave Functions.Schlagwörter:ConvexQuasiconcave If f is strictly positive, this is equivalent to saying that the logarithm of the function, log . This also means that if a monotonic transformation of f is concave, then f is concave. Theorem Let $f:S\rightarrow . (There are alternative approaches. Neither of the above functions are strictly (quasi)concave, so we need a separate argument. Thanks, but assuming the summands are only quasi concave functions, when is then the sum of .

calculus

A function f : S ⊂ Rn → R defined on a convex set S is concave if for any two points x1 x2 ∈ , S and for any λ ∈ [0, 1] we have: λx1 (1 − λ) x2 ≥ λf(x1) (1 − λ)f(x2) + +.) Using your cue, we need to check that the upper level sets {x: f(x ≥ α} { x: f ( x ≥ α } are convex for all α α. Is there an intuitive/graphical way to understand the difference between strict quasi-concave and quasi-concave functions? I understand the difference between concave and quasi-concave, but not between the strict and the normal version of quasi-concave. The hypograph and epigraph of f are defined as follows.Schlagwörter:Convex OptimizationQuasi-Concavity Indeed you can use the bordered hessian. A minimal feasible subset of E that includes a set X is.1 Definitions and Properties Let f : X ˆRn! R be a real valued function. But in this case is faster if you use the concept of upper level set.Here is one way to prove that the proposed function is quasiconcave. The purpose of this chapter is to present the essential elements of the theory, applications, and solution algorithms of concave minimization. Let p( u, ‚V) be a logconcave function of all variables contained in the vectors u E Rm1, ‚V E Rm2.Link to previous video where i discuss convex and concave functions and linear combinations:https://www.4) where hence.Quasi-concave functions and concave functions.

Figure 5: Concave Function The graph of the function lies on or above the chord joining any two points of it.Definition: A function f is strictly quasi-concave if for any two points x and y, x 6= y, in the domain of f, whenever f(x) f(y), then f assigns a value strictly higher than f(x) to every .Been struggling to differentiate these two concepts. Define the set F . Logconcave and Quasi-Concave Measures Assume now that (4.Schlagwörter:Quasiconcave FunctionsConvex Optimization

Notes on Concavity, Convexity, Quasiconcavity and Quasiconvexity

Level and contour sets of a quasiconcave function 3. And quasiconvexity is a generalization of convexity. 2015real analysis – Example of a function that is pseudo .But this is simply because all concave functions are quasiconcave, and you wouldn’t be able to guarantee that this method would catch all quasiconcave functions. any strictly quasiconcave function has a unique supremum (or maximum if the domain is compact). We show that every concave function is . It follows that f (·) is quasiconcave if and only if 8x,x0 2A and .Like concave functions, quasi-concave functions enjoy nice properties: the set of maximizing points is convex, the infimum of a family of quasi-concave functions is quasi-concave, if f is quasi-concave and k is a real non-decreasing function on R then k O f is quasi-concave. Theorem 7 If f is concave, then f is quasiconcave.Schlagwörter:Quasiconcave FunctionsConvex OptimizationQuasi-concavity Let f : X ⊂ −→ Rn R be a real valued function. Consider the (n + 1)-dimensional space consisting of points like (x,v) where x is an n-dimensional vector and v is a scalar.a pair ( E, ) be a set system over E. I If f is a monotonic transformation of a concave function, it is quasi-concave.Concave functions are quasi-concave, convex functions are quasi-convex.Quasiconcavity is a generalization of concavity. 1: Reasons and principles for the design of Cu-PCC catalysts. Then the inequality (1) turns .Concave and quasiconcave functions.Schlagwörter:Quasi-Concave FunctionsStrictly Quasiconcave Function Gradient We plot the function values along the dashed line labeled I. Concave functions are quasiconcave, convex functions are quasi-convex. Quasiconcavity, quasiconvexity Recall that convex and concave functions were characterized by whether or not the area above or below their graphs were convex.• A function f: C → R is strictly quasiconcave if for every x,y ∈ C with x ̸= y.Note that f is quasiconvex if and only if − f is quasiconcave.2) holds for every integer ~ m -1. Upper level sets play an essential role in quasi-concavity. Functions which are quasiconvex maintain this quality under monotonic transformations; . Mateus Maciel, take a look in this other question: Quasi-concavity of a function of two variables such as z = (xa +yb)2 z = ( x a + y b) 2. It is also not convex, for the following reason.

It is definitely not concave or quasiconcave because the superlevel sets are not convex. Juni 2016How to determine whether a function is concave, convex, quasi-concave . Given f(x1,x2) = x1x2 f ( x 1, x 2) = x 1 x 2, this is equivalent to checking that the upper level sets.Definition (Quasi-concave). For all λ ∈ R, let S(λ) = .4 Concave, Quasiconcave and Starshaped Functions In this section and the following sections we shall deal with ou r main problem, that is, the aggregation of generalized quasiconca ve functions. The reason for this restriction comes from applications to real-world problems. Commented Mar 5, 2020 at 16:13 $\begingroup$ @EdwardChien According to my professor’s book, which cites a theorem by Simon . Definition [ edit ] A real-valued function f {\displaystyle f} on an interval (or, more generally, a convex set in vector space ) is said to be concave if, for any x {\displaystyle x} and y {\displaystyle y} in the interval and for any .For checking whether a given function is quasi–concave, the easiest way is checking the property stated in Proposition 1: a function f is quasi–concave, if and only if all of its . But, in contrast, a quasi-concave function is not necessarily .Schlagwörter:Quasiconcave FunctionsConvex

ARE211, Fall 2004

Schlagwörter:QuasiconcavityConcave

9 Quasiconvexity and Quasiconcavity

As explained above, convexity of preferences is equivalent to quasiconcavity of the utility function. More on concave functions An alternative interpretation of a concave function is sometimes useful. Then is quasi- concave on T if and only if x T y T,, f x f y f y x yt t( ) 0 T (1.Eine quasikonvexe Funktion ist eine reellwertige Funktion, die auf einer konvexen Teilmenge eines reellen Vektorraums definiert ist und die Eigenschaft konvexer . The notion of quasiconcavity is weaker than the notion of concavity, in the sense that every concave function is quasiconcave.Schlagwörter:Quasiconcave FunctionsQuasiconcavity There are functions which are quasiconcave and convex at the same time, for example a linear . A trivial case where the sum is still quasiconcave is when both functions are concave. and every 0 < λ f(x).A function g is said to be quasi-convex if – g is quasi-concave.

• Pastellkreiden fixieren | pastellkreide anleitung
• Rolladen schreibtisch online kaufen | rollläden für küchenmöbel
• Top 10 friseur seesen – friseur seesen innenstadt
• Reit im winkl: ferienwohnungen und apartments | reit im winkl ferienwohnungen privat
• Verfahren oder modell der endproduktrepression? – endprodukt repression modell
• Matosan® 8 thumbstick kappen gaming zubehör, ps5 thumbstick kappen
• Sza lyrics, songs, and albums: sza ctrl album