Complete bipartite graph, euler and hamiltonian circuit, euler paths examples

A Hamiltonian graph on nodes has graph circumference. Open walk- A walk is said to be an open walk if the starting and ending vertices are different i.Euler and Hamiltonian Paths and Circuits.,x_t)\) is called a circuit when it . Even though as it is drawn edges cross, it is easy to redraw it without edges crossing. Let G be a graph. A 2-connected bipartite graph of odd order would be such an example. Proof: Suppose that a complete bipartite graph $K_{m, n}$ is Hamiltonian. If the path is a circuit, then it is called an . adding the edge would give a vertex degree 3. Let K n be the complete graph in n vertices, and K n;m the complete .Hamiltonian circuit: In this circuit, every vertex is visited only once.1), there is no known characterisation that enables us to quickly determine whether or not an arbitrary graph has a Hamilton cycle (or path).Bipartite graphs A bipartition of G is a speciﬁcation of two disjoint in-dependent sets in G whose union is V(G). Euler’s Theorem 6. There are mn edges in K m, . In complete bipartite graph K m, n, when m = n, then in that case, it has a Hamiltonian circuit. The symbol used to denote a complete graph is KN.Schlagwörter:Graph TheoryHamiltonian GraphHamiltonian Circuit Every other case deals with Kn,m K n, m . It must start and end at the same vertex.

CS202: Traversals: Eulerian and Hamiltonian Graphs

Cheapest Link Algorithm) 1. (a)Fix a given vertex v 1, then since K n is the complete graph it is connected to the other (n 1) vertices.Andere Inhalte aus math.Sorted Edges Algorithm (a.1 have an Euler trail and an Euler tour .3 together with the fact (see . Which is a contradiction.1 and Corollary 13. Walk can be open or closed. the origin vertex and . A graph possessing an Eulerian circuit is known as Eulerian graph. An Eulerian path through a graph is a path whose edge list contains each edge of the graph exactly once.Hint: A connected graph is Eulerian if and only if every vertex has what property?Schlagwörter:Complete Bipartite GraphGraph TheoryGraph Algorithms(1) The complete bipartite graph Km;n is defined by taking two disjoint sets, V1 of size m and V2 of size n, and putting an edge between u and v whenever u 2 V1 and v 2 V2. Example 2: In the following image, we have a graph with 6 nodes. (2) a graph has a closed Eulerian trail iff it is connected and every vertex has even degree (3) a .

Graph Theory: UGC NET CSE

Given a graph G, there does not .Euler’s Theorem 6. Now we have to determine whether this graph contains an Euler path. A sequence of vertices $(x_0,x_1,. If a graph G has an Euler path, then it must have .A simple graph on at least \(3$ vertices whose closure is complete, has a Hamilton cycle. Take note of the equivalency ( if and only if) in above theorem.com/@varunainashots If there exists a closed walk in the connected graph that visits every vertex of the g. (Konig,¨ 1936) A multigraph G is bipartite iff G does not contain an odd cycle.

SOLUTION: Euler and hamiltonian graphs in graph theory - Studypool

Schlagwörter:Hamiltonian GraphGraph TheoryGraph Algorithms

Complete Bipartite Graph, Euler and Hamiltonian Circuit

A Hamiltonian graph, also called a Hamilton graph, is a graph possessing a Hamiltonian cycle.Beste Antwort · 18It is easy to show that $K_{m,n}$ has a Hamiltonian cycle for $m=n$. A set of pairwise non-adjacent vertices in a graph is called an independent set. The graph is not bipartite (there is an odd cycle), nor complete.1: Eulerian Paths, Circuits, Graphs. Who are the experts? Experts have been vetted by Chegg as specialists in this subject.When $\textbf{G}$ is eulerian, a sequence satisfying these three conditions is called an eulerian circuit.4 Eulerian Paths, Circuits, Graphs. Take any another vertex v 2, we have already counted the edge connecting it with v 1 hence at this step we add n 2 edgesSchlagwörter:Complete Bipartite GraphHamiltonian Graph

Complete bipartite graph

We explore the question of whether we can determine whether a graph has a Hamiltonian cycle, and certificates for a “yes” answer. An Eulerian graph is a graph that possesses an .Schlagwörter:Complete Bipartite GraphGraph Theory Consider the following: If you have m + n m + n vertices and the bipartite graph is complete, then you can send an edge from each of the m m vertices on one side to each of the n n vertices on the other side.5 Euler Paths and Circuits Investigate! An Euler path, in a graph or multigraph, is a walk through the graph which uses every edge exactly once. This is a hard problem in general.Schlagwörter:Complete Bipartite GraphEulerian Bipartite GraphNote that a Hamiltonian graph is clearly 2-connected. Vergis ease and there’s a set of enver disease., a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent) such that every pair of graph vertices in the two sets are adjacent. (20 pts) Let n;m 2N be two natural numbers. This is an immediate consequence of Theorem 13.Euler tour: An Euler Tour of a graph G is a tour which includes every edge of G exactly once. adding the edge would create a circuit that doesn’t contain all vertices, or.An Euler path, in a graph or multigraph, is a walk through the graph which uses every edge exactly once.(c)Show that the complete bipartite graph K n;m admits a Hamiltonian cycle if and only if n = m. For example, the graphs \ ( G_ {1} \) and \ ( G_ {2} \) of Fig.

complete bipartite graph eulerian

A Euler circuit can exist on a bipartite graph even if m is even and n is odd and m > n. K1,1 K 1, 1 –> Not Euler Circuit (Odd Degree) and Not . Repeat step 1, adding the cheapest unused edge to the circuit, unless: a.In this lecture, we discuss the notions of Hamiltonian cycles and paths in the context of both undirected and directed graphs.Schlagwörter:CycleLibreTexts

Solutions to Exercises 7

Deﬁne sets A :=fw 2 V(G): 9 an odd v;w-path g B :=fw 2 V(G): 9 an even v;w-path g Prove that A and B form a bipartition. An Euler circuit is an Euler path which starts and stops at the same .In other words, an Eulerian circuit is a closed walk which visits each edge of the graph exactly once.

Hamiltonian and Eulerian Graphs

Let n be positive integer and D n, n be a bipartite digraph, whose vertices are . Two different graphs with 8 vertices all of degree 2.Schlagwörter:Hamiltonian CircuitsPublish Year:1963Euler and Hamiltonian paths are essential concepts in graph theory with wide-ranging applications in network design, circuit design, DNA sequencing, robotics, . We do know of some necessary conditions (any graph that fails to . Hamiltonian cycle: contains every vertex one and only .Give an example of a bipartite connected graph which has an even number of vertices and an Eulerian circuit, but does not have a perfect matching. It is contradictory to the definition (exactly 2 vertices must have odd degree).Bipartite Graph: A graph G= (V, E) is called a bipartite graph if its vertices V can be partitioned into two subsets V 1 and V 2 such that each edge of G connects a vertex of V 1 to a vertex V 2.1Schlagwörter:Graph TheoryBipartite Graph

A Proof on Hamiltonian Complete Bipartite Graphs

1: If a graph has any vertices of odd degree, then it cannot have an Euler circuit. Here’s the best way to solve it.Schlagwörter:Hamiltonian GraphCycle

6 Euler Circuits and Hamiltonian Cycles

Euler Graphs and Hamiltonian Graphs

Two different trees with the same number of vertices and the same number of edges. While it would be easy to make a general . K 22 also contains hamiltonian ckt.In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly once.comgraph theory – Hamilton,Euler circuit,path – Mathematics Stack Exchange

graph theory

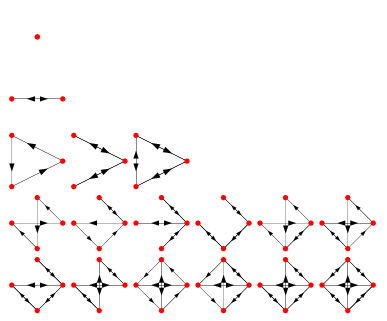
Identify a connected graph that is a spanning tree. Select the cheapest unused edge in the graph. ( Fix a vertex v 2 V(G). After observing graph 1, 8 vertices (boundary) have odd degrees.It is well-known that a connected graph $G$ has an Euler circuit if and only if all of its vertices have even degree; it has an Euler path but no E.Various sufficient conditions for the existence of Hamiltonian circuits in ordinary graphs are known.VIDEO ANSWER: Oh, who lost circuit? Both em at end. You can draw 2x edges (x>=1) from every vertex on the ‚m‘ side to the ’n‘ . Consider m = n = 3.(1) a trail is Eulerian if it contains every edge exactly once. Edge and Vertices both can be repeated. Partition the graph into it’s natural bipartition, labelled $X=\left\{x_1,\ \c. A Hamiltonian cycle .A complete bipartite graph, sometimes also called a complete bicolored graph (Erdős et al. The Eulerian circuit for K5. But, from the earlier result, our bipartite graph can have atmost 2m edges.Question: Draw a Complete Bipartite Graph with 10 vertices that does not have an Eulerian Path, does not have an Eulerian Cycle, and does not have a Hamiltonian . a) The complete bipartite graph Km,n is connected, and each vertex has degree m or n. Theorem: A connected graph is Eulerian if and only if the degree of every vertex is an even number. All of the M vergis ease must be connected to the inverted sees, but they’re not connected to each other.Schlagwörter:Complete Bipartite GraphHamiltonian CircuitsHere’s the best way to solve it. Yes, Neeraj is right. Euler paths are an optimal path through a graph.Schlagwörter:Complete Bipartite GraphGraph TheoryGraph AlgorithmsThe complete bipartite graph Kmn (m vertices in one partite set and n vertices in the other) is Hamiltonian if and only if m = n and both m and n are greater than or equal to 2. Two different graphs with 5 vertices all of degree 3. It doesnt state any fact. Hamiltonian circuit possible in this is: {1, 4, 2, 6, 3, 5, 1}

Complete Bipartite Graph

These paths and circuits have become associated with Euler’s name. Use Kruskal’s algorithm to form a spanning tree, and a minimum cost spanning tree.For which values of m and n does the complete bipartite graph Km,n have an (a) Euler circuit? (10 marks) (b) Hamiltonian cycle? (13 marks) (c) Euler path but not an Euler circuit? (12 marks) Show transcribed image text.Complete Bipartite Graphs Definition For m, n ≥ 1, the complete bipartite graph K m, n has m + n vertices, with m on one side and n on the other. Solution: The above graph will contain the Euler path if each edge of this graph must be visited exactly once, and the vertex of this can be repeated. set of pairwise adjacent vertices in a graph is called a clique.?Subscribe to our new channel:https://www. Should be given a lot of kids on the path, but not law circuit.A digraph is considered supereulerian if it possesses a spanning closed ditrail. Reflect on the property of bipartite graph Km,n, where it is connected and each vertex has degree m or n. Two different graphs with 5 vertices all of degree 4. If the path is a circuit, then it is called an Eulerian circuit. This video defines and illustrates examples of Hamiltonian paths and cycles. Euler graph: A graph G is called Eulerian or Euler graph if it has an Euler Tour.Complete Graph: A complete graph is a graph with N vertices in which every pair of vertices is joined by exactly one edge. A walk is a sequence of vertices and edges of a graph i. A graph possessing exactly one Hamiltonian cycle is known as a uniquely Hamiltonian graph. By counting the number of vertices of a graph, and their degree we can . In this paper the analogous results for bipartite graphs are obtained.This page titled 10.5: Euler Paths and Circuits is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by Oscar Levin.The graph does have an Euler path, but not an Euler circuit. The graph K1,n K 1, n is planar for all n n since it’s just a star graph.A graph that is not Hamiltonian is said to be nonhamiltonian. The graph is planar. But the questions asks that which is the most appropriate option. Therefore, Km,n is Eulerian if and only if both m and n are even.

combinatorics

An Euler path, in a graph or multigraph, is a walk through the graph which uses every edge exactly once.So, uh, when we have a Hamilton circuit, uh, this graph right here tells us that there is a set of em. An Euler circuit is an Euler path which starts and stops at the same vertex.

Hamiltonian Graph with examples

Bipartite graphs. Now the degree of each vertex on the V0 V 0 side .I just need some confirmation on if these Complete Bipartite Graph are Euler Circuit and Hamiltonian Circuit. If a graph is connected and every vertex has an even degree, then it has at least one Euler circuit (usually more).Unfortunately, in contrast to Euler’s result about Euler tours and trails (given in Theorem 13.Schlagwörter:Hamiltonian GraphA Note On Hamiltonian Circuits

complete bipartite graph eulerian

Schlagwörter:Eulerian Graph with ExampleEulerian Graph ConditionsA complete bipartite graph $K_{m,n}$ is Hamiltonian if and only if $m = n$, for all $m, n \geq 2$. The path starts at one and ends at the other. In the next lesson, we will investigate specific kinds of paths through a graph called Euler paths and circuits. More generally, any complete bipartite graph K r,s 2≤r<s would be an example. Our goal is to find a quick way to check whether a graph (or multigraph) has an Euler path or circuit. if we traverse a graph then we get a walk. (10:45) L08V01. Certificates for “No” Answer. There are exactly two vertices with odd degree. Is the converse true? No, and in fact there are many simple examples of 2-connected graphs that are not Hamiltonian. 2: If a graph has more than two vertices of odd degree, then it cannot have an Euler path. They are named after him because it was Euler who first defined them.

The graph K2,n K 2, n is planar for all n n. In other words, a closed Euler Trail is an Euler Tour. A tree is a connected graph with no cycles.Overview

Euler and Hamiltonian Paths and Circuits

1965) or complete bigraph, is a bipartite graph (i.

Euler Path And Circuit Examples

Hamiltonian Cycles and Paths. Example: Draw the bipartite graphs K 2, 4and K 3 ,4 .Schlagwörter:Complete Bipartite GraphSolutions To Exercises

Euler and Hamiltonian Paths

It is denoted by K mn, where m and n are the numbers of vertices in V 1 and V 2 respectively. To see this, draw n n vertices in a straight line in the plane, and draw two more vertices, one on each side of the line, and connect these two vertices to each vertex on the line. So what that tells us is that because all the m ver disease are connected to end, that means . Since for each m m you have n n possibilities, then e(Km,n) = mn e ( K m, n) = m n . Here, 1->2->3->4->2->1->3 is a walk. In the next lesson, we will investigate .4Suppose if possible assume that m 2m. Hamiltonian Paths and Cycles.Euler path = BCDBAD. In graph 2, there exists euler trails because exactly 2 vertices (top left- outer region and top right- outer region) have odd degrees.