Definitionsbereich und definitionslücken | definitionsbereich bestimmen mit formel

welche man nicht einsetzen darf. Entweder nähert sich der Graph dort einer senkrechten Asymptote an, dann liegt eine Polstelle vor, oder es liegt eine hebbare .Bei einer Definitionslücke handelt es sich um Punkte einer Funktion, die außerhalb des Definitionsbereichs liegen. Der Fall einer hebbaren Definitionslücke ist dann gegeben, . Die Periode ist genauso wie bei der Cosinus- und Sinusfunktion π Definitionsbereich: D=ℝ\{(ℤ+1/2)·π} (das bedeutet einfach, dass im Definitionsbereich ganz ℝ ist, außer alle vielfachen von π, die durch . die Definition des Wortes, Lehrsatzes ist schwer.Der Definitionsbereich einer algebraischen Funktion ist eine Menge an reellen Zahlen, für die die Funktion definiert ist.Der Begriff hebbar bedeutet in diesem Zusammenhang, dass die Definitionslücke behoben und damit der Definitionsbereich erweitert werden kann. ( x) und Eine Division durch Null ist nicht erlaubt! sind alle Nullstellen der Kosinusfunktion Definitionslücken der Tangensfunktion. Natürlich bist du bereits mit Funktionsgleichungen wie zum Beispiel f(x) = x2 + 2x– 1 vertraut. Definitionslücken sind Werte, die in eine Funktion nicht .

Definitionsbereich bestimmen: Funktion & Aufgaben

f (x), rauskommen kann, wenn man jede Zahl aus der Definitionsmenge in die Funktion (für x) eingesetzt hat. Der Definitionsbereich Df einer Funktion f(x) ist die Menge aller für die die Funktion gebildet werden kann. In dem mathematischen Teilgebiet der Analysis hat eine Funktion Definitionslücken, wenn einzelne Punkte aus ihrem Definitionsbereich ausgeschlossen sind. Mathematischer Grundbegriff.Das spricht man so aus: Der Definitionsbereich besteht aus allen x aus den rationalen Zahlen für die gilt, dass x ungleich 0 ist.

Definitionslücken in Mathematik

Der Definitionsbereich ist die Menge aller .

Hebbare Definitionslücke verstehen ⇒ Mathe Lerntipps!

Bei einer gebrochenrationalen Funktion ist das die . Unter einer Definitionslücke versteht man einzelne Punkte einer Funktion, die aus dem Definitionsbereich ausgeschlossen sind. Hier hätte man es also wie direkt gesehen mit D = ℝ \ {3} zu tun und nicht etwa mit D = ℝ. ist Definitionslücke von f(x)⇔q(xi)=0.Definitionsmenge bestimmen.Die Definitionsmenge einer Funktion ist der Bereich, wo die Funktion definiert ist, also Funktionswerte hat.

Definitionslücke

Definitionsbereich und Definitionsmenge Aufgaben / Übungen

Eine Definitionslücke ist eine Stelle, wo man keine. Kurvendiskussion gebrochenrationale Funktion: Nullstelle, Polstellen, Verhalten an den Definitionslücken, schräge / waagrechte Asymptoten, Funktionsgraph skizzieren Dieses sprachliche Zeichen wird Definiendum genannt. Hier klicken zum Ausklappen. Die Tangens-Funktion weist nämlich Definitionslücken auf.In diesem Artikel geht es um Definitionslücken, hebbare Definitionslücken, Pole und Nullstellen.

Definitionsmenge einer Funktion

Definitionslücken – das sind Stellen, an denen .) Bestimmen Sie die maximale Definitionsmenge der Funktionen f und g.Definitionslücken und deren Nachweis. Am besten merkst du dir das einfach! Beim Tangens ist es ein wenig komplizierter.heißt gebrochenrationale Funktion.

Hebbare Definitionsluecke - YouTube

(Nullstellen des Nenners) Dort ist die Funktion also nicht definiert. direkt ins Video springen Graph mit Definitionslücke. Man unterscheidet zwischen Polstellen und hebbaren .Die Definitionsmenge D f ist die Menge aller x -Werte, die in die Funktion f eingesetzt werden dürfen. Bei der Betrachtung der Ordnung einer Polstelle ist es wichtig, dass man den Bruch zunächst vollständig kürzt. Eine Definitionslücke, ist wie der name schon sagt ein lücke im Definitionsbereich der Funktion. Zu den ganzrationalen Funktionen zählen u. zur Definitionsmenge bekommt ihr hier Übungen zum selbst Rechnen. Definitionslücken und Definitionsbereiche bestimmen. Aber es geht auch komplizierter, und zwar mit der Funktion f (x) = (x +1) 1.

Trigonometrische Funktionen

) Untersuchen Sie, ob bei den Funktionen f und g Asymptoten vorhanden sind und geben Sie gegebenfalls . Wenn man sich mit einer Kurvendiskussion befassen will oder auch in anderen Bereichen, so ist es oft notwendig, sich um die . Den Zähler kannst Du für den Definitionsbereich ignorieren.Die Definitionsmenge ist eine sehr wichtige Angabe, wenn du eine Funktion genau definieren sollst.Es gilt zu beachten, dass die Definitionsmenge immer bezüglich der Ursprungsfunktion zu untersuchen ist. Ein weiteres Beispiel ist: $ f(x) = \frac{1}{x} $ Mit dem Definitionsbereich kannst du jetzt weiter den Wertebereich bestimmen. Eine gebrochenrationale Funktion ist eine Funktion, bei der sich sowohl im Zähler als auch im Nenner eines Bruchs eine ganzrationale Funktion befindet.Playlist Verhalten im Unendlichen, Definitionslücken, Polstellen: https://www. Sollst du aber die ursprüngliche Funktion mit Definitionslücke zeichnen, dann markierst du die hebbare Definitionslücke durch .Definitionslücke, Polstelle, Hebbare Lücke, Übersicht Wenn noch spezielle Fragen sind: https://www. Für eine exakte Bestimmung brauchen wir jedoch noch zwei weitere Angaben, und zwar die Definitionsmenge und den Wertebereich der Funktion.

Definitionsarten: Definition

Die Definitionslücken sind die Stellen, an denen man durch null teilen müsste oder . Unter der Ordnung einer Polstelle versteht man die Vielfachheit ihrer Nullstelle. Schritt 1: Grundsätzlich ist der Nenner der Funktion zu betrachten und dieser mit 0 gleichzusetzen. Für die Tangensfunktion gilt: D f = R ∖ { π 2 + k ⋅ π, k ∈ Z } Begründung.

Definitionsmenge

Dies ist insbesondere wichtig, wenn es um . Eine Definitionslücke ist eine Stelle, an der die Funktion nicht definiert ist.

Arten von Definitionslücken - Teil 2 - YouTube

Beispiel: y = sin (x) ist überall definiert, y= sin (x) / x. Die Wertemenge gibt an, was alles für y, bzw.Du willst wissen, was die Definitionsmenge ist und wie du sie ganz leicht bestimmen kannst? Dann bist du hier genau richtig! .Der Definitionsbereich – auch Definitionsmenge genannt – gibt an, welche Zahlen man in eine Funktion einsetzen darf bzw. f:x → x / (1+5x) g:x → (x+2) / (x 2 +x-2) b.Definitionsbereich. Da beispielsweise das Teilen durch 0 nicht definiert ist, . Wertebereich: Du siehst am Graphen, dass dieser alle y-Werte annimmt.

Definitionsbereich • Definitionsbereich bestimmen und angeben · [mit Video]

Im Folgenden erkläre ich dir kurz, wie der Rechner funktioniert. Werte berechnen kann. Bei der Funktion f(x) . Dazu musst du . Skizzieren Sie den Graphen und prüfen Sie Ihre Skizze mit Hilfe eines Funktionsplotters. Bei der Bestimmung des Definitonsbereichs mögliche Definitionslücken oder Einschränkungen des Definitonsbereichs zu beachten: Nenner .hebbare Definitionslücke.Die Definitionslücken sind die Stellen, an denen man durch null teilen müsste oder Ähnliches, beispielsweise bei gebrochenrationalen Funktionen.Definitionsbereich und Definitionslücken Der Definitionsbereich gibt an, für welche Zahlen eine Funktion definiert ist. Definitionsbereich: Die Variable x steht nicht im Nenner, also ist der Definitionsbereich ganz Q ℚ.

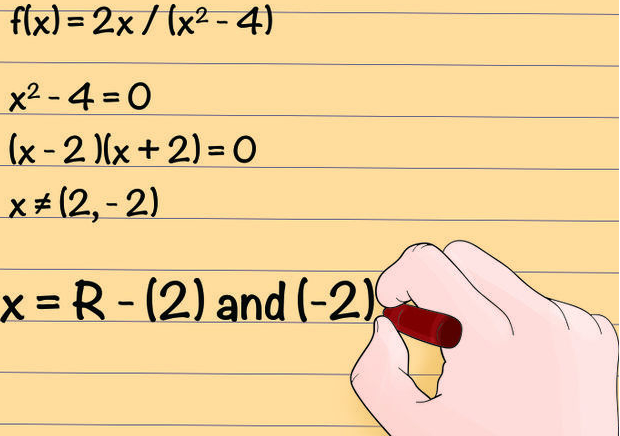
Definitionsbereich

Außerdem ist der Definitionsbereich eine sehr wichtige Angabe, wenn du Funktionen genau .

Wertebereich • Wertemenge bestimmen · [mit Video]

Vorgehensweise: Nullstellen des Nenners bestimmen. Auch hier guckt man am besten, was nicht rauskommen kann, achtet dabei vor allem auf Folgendes: Wird x mit einer geraden Zahl potenziert, können nur positive Zahlen (und die 0 . Gib für folgende Funktionen die maximale Definitionsmenge an . \[k(x) = \frac{5}{x^2 + 3x – 2x – 6} \] Lösung. f ( x) = x 4 x − 1.Ordnung einer Polstelle.

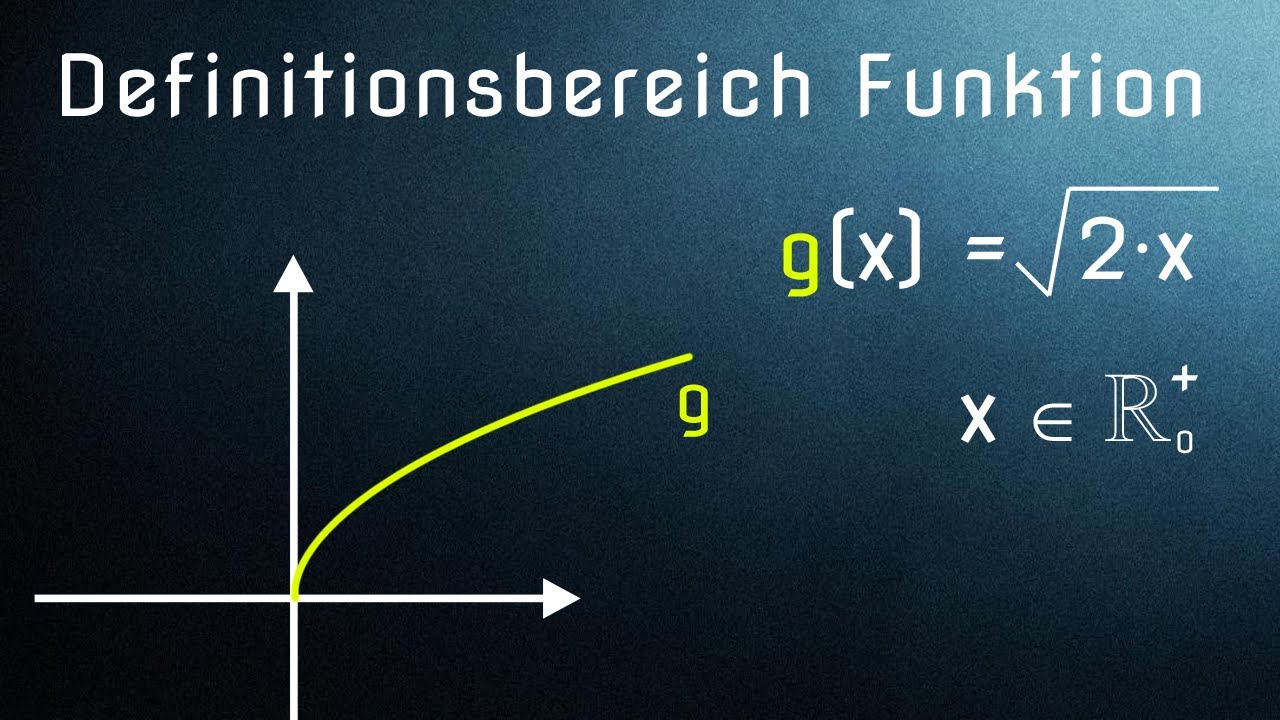
Maximalen Definitionsbereich einer Funktion bestimmen - YouTube

Kurz: Alle die man in die Funktion einsetzen darf.In diesem Kapitel wird behandelt, wie mit Funktionen dieser Art umzugehen ist und wie sie sich verhalten, wenn die Funktionswerte gegen – ∞ und + ∞ laufen. Kurz: Alle die man in die Funktion .Um den Definitionsbereich einer Funktion zu bestimmen, muss man sie auf Definitionslücken prüfen. Rechts und links der Polstelle steigen die y y y y – Werte in Richtung \pm \infty ± ∞ \pm \infty ± ∞.Hier erfährst du, welche Eigenschaften gebrochen-rationale Funktion haben, wie du ihren Definitionsbereich bestimmen und ihren Graphen erkennen kannst. Finde die Nullstellen der Funktion.Gebrochenrationale Funktion: Maximale Definitionsmenge angeben, Funktionsgraph zuordnen und begründen, Funktionsterm zuordnen. Nullstellen des Zählers bestimmen: Resultiert dieselbe Nullstelle wie im Nenner, liegt eine mögliche . Schritt: Finde die Definitionslücken der Funktion heraus. Außerdem wird dir gezeigt, wie du den Graphen einer Funktion mit der Funktionsgleichung vom Typ y = a x + c + d zeichnen kannst. Definitionslücken. Beispiel Aufgabe: Behebe die hebbare Definitionslücke der Funktion. Mach dir keine Sorgen: Du musst weder Mathe- noch Technik-Freak sein, um mit dem Teil zurechtzukommen.eine exakte, (un)genaue, falsche, richtige, allgemeine Definition geben. Die 0 nennst du dann auch Definitionslücke.Definitionslücken sind Stellen, die nicht im Definitionsbereich enthalten sind, weil der Nenner q(x) dafür Null werden würde: xi. Auch im Graphen kannst du die Definitionslücke bei x = 0 erkennen.com/playlist?list=PLrKeeNRUr2UwF-iUR2HOBZSBebvFk_uynÜbungsblätter und m.Definitionslücken sind an den Stellen, an denen die Kosinusfunktion 0 ist, da man ja nicht durch 0 teilen darf.Mathematischer Grundbegriff. Auch das kannst du sehr schön am Funktionsgraphen erkennen.Eine Definitionslücke, die durch Kürzen des Funktionsterms behoben werden kann und dadurch den Definitionsbereich erweitert, heißt hebbaren Definitionslücke. Man spricht hier übrigens von einer „hebbaren Definitionslücke“.

Definitionsbereich einer Funktion

(Online-Rechner) Mit meinem Online-Rechner kannst du ganz einfach den Definitionsbereich einer Funktion bestimmen.

Definitionsbereich

Die Definitionslücken .Geschätzte Lesezeit: 50 Sekunden

Definitionsbereich / Definitionsmenge

de Playlists zu allen Mathe-Themen findet ihr . mit dem Definitionsbereich D f ⊆ R, wobei Z ( x) und N ( x) Polynome in x sind und N ( x) einen Grad größer Null besitzt, heißt gebrochen-rationale Funktion.

Aufgaben zur Bestimmung von Definitionsmengen

Geben Sie den maximal möglichen Definitionsbereich an und untersuchen Sie das Verhalten des Graphen an der Definitionslücke. Alle Stellen x 0, für die die Stetigkeitskriterien nicht zutreffen, heißen Unstetigkeitsstellen oder auch Definitionslücken. \begin{align} 0 &= x^2 + 3x – 2x – 6 \end{align}Damit erweitert man den Definitionsbereich, denn die behobene Lücke muss dann nicht mehr vom Definitionsbereich ausgeschlossen werden. differenzierbare Funktionen.Der Definitionsbereich umfasst alle Zahlen, die du für x einsetzen kannst. Diese Stellen .Eine Definition ist die Angabe der Bedeutung eines sprachlichen Zeichens – eines Wortes, Symbols oder einer Abkürzung.Polstellen und hebbare Definitionslücken gebrochen rationaler Funktionen. Schaue also, was du nicht in die Funktion einsetzen darfst. Schritt: Bestimme alle Extrempunkte der Funktion. Wir lösen die Gleichung x +1=0 und erhalten, wie erwartet, x = -1. Es handelt sich um eine Polstelle 1. Man sagt: Die . Jetzt, wo du die Definition und Schreibweise der Definitionsmenge kennst, kannst du dir anschauen, wie du die Definitionsmenge bestimmen kannst. Löst die Übungen selbst, ohne dabei zu schummeln. Üblicherweise geht es dabei um reelle, stetige bzw. Im Nenner darf zum Beispiel nie 0 stehen. Der Nenner besitzt bei x = 0 eine einfache Nullstelle. f ( x) = x + 4 x 3 + x.Alle x-Werte, für die die Nennerfunktion den Wert Null annimmt, werden als Definitionslücken bezeichnet. Etymologisches Wörterbuch (Wolfgang Pfeifer) . Eine Funktion der Form. Bei dieser Funktion ist nicht sofort ersichtlich, dass sie sich auch als Bruch darstellen lässt.Bestimme die Definitionsmenge für die folgende Funktion. Dabei erkläre ich die Begriffe zunächst und zeige anhand von Beispielen wie man damit umgeht. Das heißt, du erhältst als Ergebnis alle Zahlen aus Q ℚ.

Tangensfunktion

Dadurch entstehen sog. Es geht darum Fragen und Übungen zu lösen. Definitionsmenge Schreibweise .Der Definitionsbereich für trigonometrische Funktionen wie die Sinus- oder die Cosinus-Funktion ist sehr einfach: D = R.Definitionslücke.Bestimme den Definitionsbereich der Funktion. Also an den Nullstellen der Kosinusfunktion.Bestimme den Definitions- und Wertebereich der Funktion f(x) = 2x f ( x) = 2 x.Definitionslücken und Asymptoten.

Definitionsmenge • Definitionsmenge bestimmen · [mit Video]

Um nun rechnerisch die Definitionslücke zu finden, setzen wir den Nenner gleich Null. Geben Sie die Art der Definitionslücken an, ob es sich um Polstellen oder um hebbare Definitionslücken handelt.Übe und vertiefe mit diesen unterschiedlichen Aufgaben dein Wissen zur Bestimmung von Definitionsmengen. Sie treten meistens bei gebrochenrationalen Funktion auf, wo an einer Stelle der Nenner Null wird und da man durch Null nicht teilen darf .Einführung Definitionsmenge einer Funktion.

Definitionsbereich bestimmen

Bestimme die Art der Definitionslücken. Ist der Grad des Zählers Z ( x) der gebrochen-rationalen Funktion f kleiner als der Grad des Nenners N ( x), so heißt die .Übungsaufgaben Definitionsbereich: Zum Definitionsbereich bzw. lineare Funktionen und quadratische Funktionen. Wer eine Übung oder Frage nicht mag, der kann auch auf überspringen klicken und damit zur .Die $x$-Werte, für die der Nenner gleich Null wird, müssen wir aus dem Definitionsbereich ausschließen. hat bei x = 0 eine Definitionslücke.