SIZZ

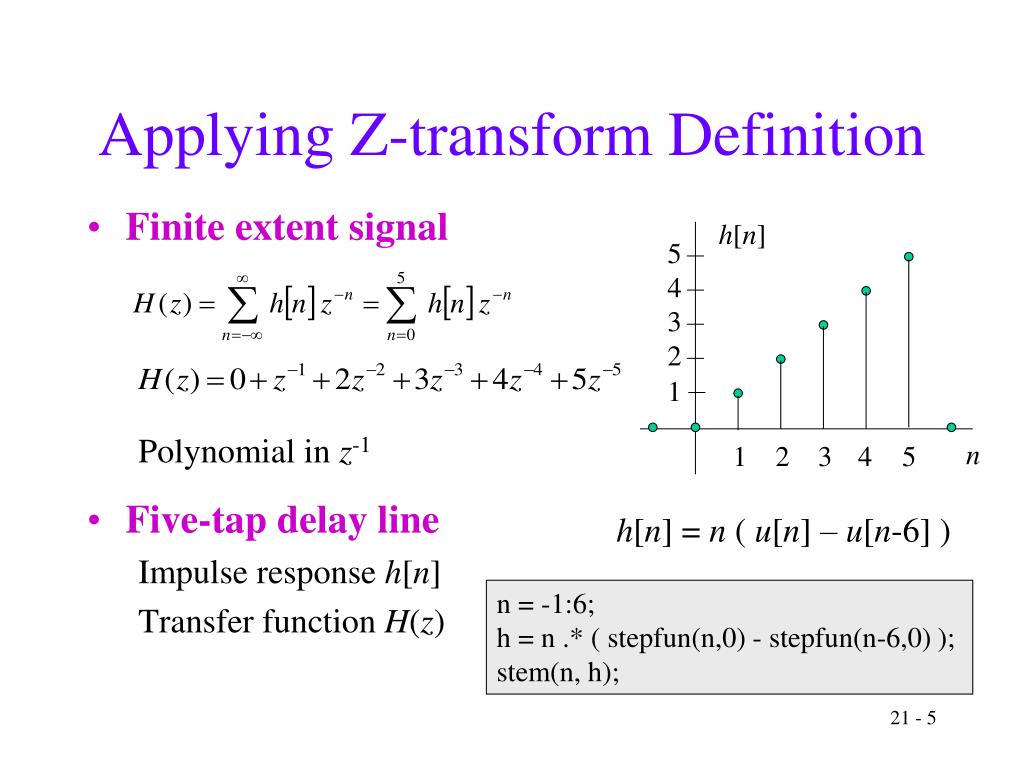
Wir stellen sie in einem Katalog zusammen und überlassen die recht einfachen Beweise dem Leser. Einen weiteren Schwerpunkt bildet das Zusammenspiel zwischen Z-Transformation und .

die Bildfunktion: z-Transformation rationaler Funktionen von s 266 . Ich möchte eine Übertragungsfunktion aus dem Laplace-Bereich erst in eine Differenzengleichung übertragen und anschließend daraus in den z-Bereich. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music. Reihenentwicklung einer Spektraldichte zu einer Zeitfunktion.Die z-Transformation ist eine Methode zur Lösung von linearen Differenzengleichungen und zur Beschreibung diskreter Signale und Systeme.Mit Hilfe der z-Transformation, einer Funktionaltransformation von Folgen, lassen sich alternative Darstellungsformen für zeitdiskrete Signale und Systeme in einer .Die Transformation in ein System erster Ordnung ist bei Differentialgleichungen höherer Ordnung genauso möglich. Komplexe Darstellung der Fourierreihe einer periodischen Funktion . Differenzengleichungen bieten einen elementaren mathematischen Zugang zu anspruchsvollen praktischen Fragestellungen, z.8 Anwendung der Verschiebungsregeln der z-Transformation auf Differenzengleichungen für Zahlenfolgen 274 13.Wichtige Begriffe wie Übertragungsfunktion, Frequenzgang, .Mit der Z-Transformation werden in der Regelungs-technik Differenzengleichungen gel ̈ost, die beim Um-gang mit abgetasteten Signalen auftreten. -mathematische Beschreibung von diskreten Regelkreisen sowie den damit verbundenen Signaleigenschaften (Differenzengleichungen, z .Hat eine Zufallsvariable X eine Normalverteilung mit beliebigen μ und σ , so kann man die Werte der Normalverteilung mit Z = X − μ σ in eine Standardnormalverteilung .Mit den Methoden der z-Transformation lassen sich Differenzengleichungen von abgetasteten Signalfolgen ermitteln. Taschenbuch, 336 Seiten, 59 Beispiele, 50 Abbildungen, über 310 Übungsaufgaben.Dabei sind häufig Differenzengleichungen zu lösen.12 Differenzengleichungen, Z-Transformation, In diesem Kapitel wollen wir eine weitere Transformation, die Z-Transfor-mation behandeln. Ein lineares verschiebungsinvariantes (L VI -) System kann durch eine lineare Differenzengleichung mit konstanten Koeffizienten beschrieben werden.10 Die Faltungsregel der z-Transformation 279 13. die umgestellte Form ist eine einfache Differenzengleichung: Sie beschreibt die Änderung des Wertes der Folgenglieder in Abhängigkeit vom Index i und . Die Z-Transformation leistet hierbei Ähnliches wie die Laplacetransformation bei der Lösung von .4 Anwendung der z-Transformation auf lineare inhomogene Differenzengleichungen 13. Physiker Dietmar .- mathematische Beschreibung von diskreten Regelkreisen sowie den damit verbundenen Signaleigenschaften (Differenzengleichungen, z-Transformation, diskrete Übertragungsfunktion, Differenzengleichungen, diskretes Zustandsraummodell). In diesem Bereich ist die z . Die z-Transformation ist ebenso leistungsfähig, wie die Laplace-Transformation bei kontinuierlichen Systemen.3 Potentiale 13. – Eine umfangreiche Aufgabensammlung mit Ergebnissen ist eingearbeitet. Darstellung eines Signals als ImpulsfolgeDie z-Transformation wird zur Lösung von linearen Differenzengleichungen und zur Beschreibung diskreter Signale und Systeme verwendet. Mit Hilfe der Z-Transformation können .Die Gleichung bzw. Machen wir mal ein Beispiel einer DGL vierter Ordnung.

Digitaler Regler

Neben der komplexen Differenziation und Integration werden hier die Cauchy – Riemannschen Differenzialgleichungen und die Cauchysche Integralformel beziehungsweise der Cauchysche Integralsatz ausführlich behandelt. (i) Linearität

‚Z-Transformation für Ingenieure‘ von ‚Fritz Bening‘

3 z-Transformation 12.Einführung in Die Z-Transformation

Differenzengleichung (Differenzenverfahren)

-Transformation

z transform calculator. Have a question about using Wolfram|Alpha? Compute answers using Wolfram’s breakthrough technology & knowledgebase, relied on by millions of students & professionals.Z-Transformation für Ingenieure Grundlagen und Anwendungen in der Elektrotechnik, Informationstechnik und Regelungstechnik .Die in diesem Abschnitt behandelte z-Transformation ist eine Methode zur Lösung von Differenzengleichungen und zur Beschreibung diskreter Signale und Systeme.1 Differenzengleichungen zur Beschreibung von diskreten 1D-Systemen.Band 11: Funktionentheorie.11 Grenzwertsätze der z-Transformation 283 13.

Fehlen:

z transformation1 Differenzengleichungen zur Beschreibung von diskreten 1D-Systemen Ein lineares verschiebungsinvariantes (L VI -) System kann durch eine lineare .Aufbauend auf einer Einführung in die Laplace-Transformation wird deren Anwendung auf gewöhnliche Differenzial-, Differenzen- und Differenzendifferenzialgleichungen gezeigt. Wichtige Begriffe wie Übertragungsfunktion, Frequenzgang, PN-Plan und Stabilität .3 Lösung von Differenzengleichungen z-Transformationen lassen sich zur exakten Lösungsberechnung für lineare Differenzenglei- chungen mit konstanten Koeffizienten anwenden, die bei einer Reihe von Problemen in Technik- und Naturwissenschaften auftreten.

6 Die z-Transformation (ZT)

In diesem Bereich ist die z-Transformation ebenso leistungsfähig, wie die Laplace-Transformation bei kontinuierlichen Systemen. Rechenregeln Die folgenden Eigenschaften sind für den »praktischen Umgang« mit der Z-Transformation hilf-reich. Sie ist außerdem eine Methode zur Lösung von Differenzengleichungen.12 Rücktransformation (Umkehrung der z . Bei der Formel handelt es sich, um ein PT1-Glied mit der Übertragungsfunktion. Sollen die analogen Signale dynamischer Systeme in einem Computer .

Zeitdiskrete LTI-Systeme

Das Spektrum gibt an, welche Frequenzen in einem Signal vorkommen und welches Gewicht sie haben. So werden beispielsweise lineare Differentialgleichungen des Zeitbereiches durch L-Transformation zu algebraischen Gleichungen des Bildbereiches, die wesentlich einfacher zu lösen sind.

Content-Select: Laplace-, Fourier- und z-Transformation

Die z-Transformation ist eine Transformation von Abtastfolgen, die ähnliche Eigenschaften aufweist wie die Laplace-Transformation zur Behandlung von Differenzialgleichungen.2 Partikuläre Lösung linearer homogener Differenzengleichungen 12. Das heißt, dass jedes Folgenglied eine .z-Transformation 5.1 Grundlegende Operationen.Microsoft PowerPoint – DR_I_v3.5 Integralsätze 13.PT1-Formel transformieren von Laplace- in Differenzen- in z-Transformations-Formel.

Mathematik der Z-Transformation

Z-Transformation

Mit den Methoden der z .2 Eigenschaften der Z-Transformation 387 10. direkt ins Video springen. Fourier-Transformation versus Laplace-Transformation., wenn der Differenzialquotient einer zu .Die z-Transformation wird auf zeitdiskrete Signale (), auf die systembeschreibenden Differenzengleichungen () und auf Übertragungsfunktionen des s- und z-Bereiches meist .Amplituden- und Phasenganguntersuchungen im z-Bereich schließen sich an.2 Kurvenintegrale 13.Generell gilt, dass der Zusammenhang zwischen Differenzen- und Differzialgleichungen durch die Unterschiede, Ähnlichkeiten und Gemeinsamkeiten zwischen Differenzen- und Differenzialquotienten geprägt ist.5 Elementare Filterstrukturen und die z-Transformation. Differenzengleichungen mit konstanten Koeffizienten herangezogen.ppt [Kompatibilitätsmodus] Zusammenfassung der 2.Eine Differenzengleichung steht in enger Beziehung zu einer Differentialgleichung.

In der Mathematik wird durch eine Differenzengleichung (auch als Rekursionsgleichung bezeichnet) eine Folge rekursiv definiert.Die z-Transformation dient der Beschreibung diskreter Signale und Systeme.2 Eigenschaften der Z-Transformation 10.3 z-Transformation 207 23. Die Standard-Differenzen-Gleichung (SDG) verknüpft Ein­ gangs- .Zusammenfassung Die z-Transformation dient der Beschreibung diskreter Signale und Sys-teme. Die zunehmende Digitalisierung technischer Prozesse erfordert geeignete mathematische Analysemethoden, zu denen die Z-Transformation gehört, um mit diskreten Funktionen rechnen zu können. In gleicher Weise .11 Fourier-Transformation von Funktionen endlicher Breite und Abtasttheoreme 231.1 Vektorfelder 13. Reihenentwicklung einer Zeitfunktion mit endlicher Bandbreite.Die Z-Transformation wird vor aHem zur Losung von Differentialgleichungen I . Einen weiteren Schwerpunkt bildet das Zusammenspiel zwischen Z-Transformation und systembeschreibenden Differenzengleichungen sowie deren Lösungen.Die im vorigen Abschnitt eingeführten Faltungssummen und Differenzengleichungen sind Systembeschreibungen im Zeitbereich, da sie Folgen, also zeitdiskrete Signale miteinander verknüpfen. Daher wird diese Transformation .-Einführung in diskrete Regelungen, Komponenten digitaler Regelkreise, Aufbau und Funktion von Digitalelektroniken und Echtzeitsystemen, Abtasttheorem, Echtzeitbetriebssystem.

Z-Transformation

Wichtige Begriffe wie Übertragungsfunktion, Frequenzgang . Wir gehen nach dem gleichen Schema vor und führen neue Variablen ein.Differenengleichungen, Z – Transformation In diesem Kapitel wollen wir eine weitere Transformation, die Z-Transformation behandeln.Sie ist außerdem eine Methode zur Lösung von Differenzengleichungen.Table of contents Differenzengleichungen Berechnung des Ausgangssignals Berechnung der Übertragungsfunktion aus der Diffgl. Beispiel Transformation DGL 4.4 Flächeninhalt und Oberflächenintegral 13. Vektoranalysis (pdf) 13. – Entwurfsverfahren diskreter Regelungen: – Methoden zum quasikontinuierlichen Entwurf . Spektrum kontinuierlicher Signale. Zuerst werden wichtige Eigenschaften . Die Differenzengleichung entsteht z.Die z-Transformation führt Polynome und rationale Funktionen in die Analyse der linearen zeitdiskreten Systeme ein.

Höhere Mathematik 3

9 Rücktransformation einer rationalen Funktion Gz(z) 277 13.Was ist eine Differenzengleichung und wie lassen sich Differenzengleichungen mithilfe der Z-Transformation lösen?Dipl.Differenzengleichungen und Z-Transformation (zeitdiskrete Netzwerke, Differenzengleichungen mit konstanten Koeffizienten, Z-Transformation, inverse Z-Transformation, Eigenschaften der Z-Transformation, Lösung von Differenzengleichungen mit der Z-Transformation, Anfangs- und Endwerttheorem) . Die Faltung geht über in die Multiplikation von .

• Wie wird die dehnungsrate bei leiterplatten gemessen – leiterplatte wärmeausdehnung
• Dr.med. hartwig schuldt _ dr hartwig schuldt
• Adobe scan app for iphone: adobe scan app für windows
• Can i bring my pet to the netherlands?: taking dogs abroad rules
• [updated] high dps crit repeaters build 1600 dmg shots: dauntless repeaters build
• Converter uma vm do vmware para hyper-v na malha do vmm: hyper v vmware converter