Divisibilité par 7 et congruence

Nombres premiers.http://jaicompris.

DIVISIBILITÉ

La démonstration emploie la . On peut aller même plus loin et démontrer des critères de divisibilité: il s’agit de règles qui . a a ; b b est un diviseur de. On pense à développer (a + b) 7 avec la formule du binôme. C’est une actualité mathématique peu commune, un enfant de 12 ans, Chika Ofili, a su découvrir un critère de divisibilité par 7 assez simple. D’après la question précédente, on a : 1000 12 13≡ ( ), soit 10 12 133 ≡ ( ).Définition 1: Soit a et b deux entiers relatifs. Le quotient est égal à 5. Donc 24 est divisible par 3.DIVISIBILITÉ par 73, 101, 111, 137 .

Exercices corrigés : Divisibilité

$P(0)$ est vraie. Démontrons par exemple que est divisible par , comme on a et on déduit que ce qui prouve que est divisible par .TS spé maths- 13 divise 2^70+3^70 et 11 div. Pour $n=0$, $3^{2\times 0+1}+2^{4 \times 0+2} = 3 + 4 = 7$ qui est bien divisible par 7. Aller à: Qui est en ligne.Schlagwörter:Critère De DivisibilitéLes Unités Aux Dizaines carpediem re : Divisibilité et congruence 13-10-15 à 19:26.Le reste de la division euclidienne de 1000 par 13 est égal à 12. Ces critères sont exposés sans démonstration.On se donne alors deux entiers a et b et on considère la fonction f: x ↦ ax + b.[TS]Spe-Arithmétique-Divisibilité et congruence. Pour les valeurs de a et b de 2 à 5, la colonne de droite vérifie bine cette propriété.frTwitter : ht. Si a – b est divisible par n, on dit que a et b sont congrus .Dans cette vidéo, nous allons voir L’ESSENTIEL a connaitre en ce qui concerne les notions de divisibilité et de congruence dans Z en Arithmétique.php- Démontrer un critère de divisibilité par 7 en utilisant les . Exemples : Pour vérifier, par exemple, que 826 413 . Définition : Soit et deux entiers relatifs.Propriétés : Soit a, a ′, b, b ′ et c des entiers relatifs et n un entier naturel non nul.Les critères de divisibilité sont des règles qui permettent de déterminer rapidement si un nombre entier (un nombre sans décimale ni fraction) est divisible par tel ou tel chiffre ou nombre. Démontrer que $a$ et $b$ sont divisibles par $7$. Maths expertes Divisibilité et .

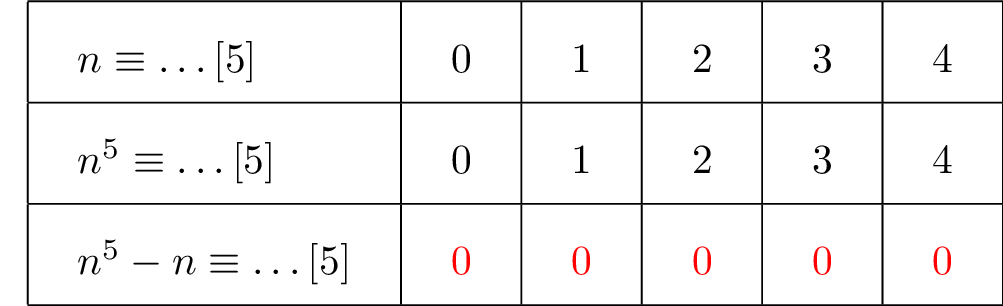
$Congruences et équations - Divisibilité dans $\\mathbb{Z}$ et ...$

Dans ces conditions, on dit que a est un multiple de b et b est un . a et b sont congrus modulo n si et seulement si b − a est divisible par n.frTwitter : http. Nous verrons la . a) Multiples et diviseurs d’un entier relatif.maths-et-tiques.Définition : Soit a et b deux entiers relatifs.Pour comprendre les congruences, nous avons besoin d’un entier naturel non nul n, et de deux entiers relatifs a et b.com/lycee/math/arithmetique/congruence-Z.Dans un premier temps, nous allons revoir la notion de divisibilité dans $\mathbb{Z}$ et la division euclidienne qui sera étendue aux nombres entiers relatifs. Nos experts chevronnés sont joignables par téléphone et par e-mail pour répondre à toutes vos questions.Une solution pr un exercice demandant de montrer qu une expression est divisible par 7 par récurrence #récurrence#divisibilité#mathématique#1ere_bac par Anonyme » Sam 30 Avr 2005 17:00 2 Réponses 882 Vues Dernier message par Anonyme Sam 30 Avr 2005 17:00 Retourner vers Lycée.

ARITHMETIQUE 1/4: DIVISIBILITE ET CONGRUENCE

Lichtenberg 2012-2013 Version d’août 2012 2.Yvan Monka – Académie de Strasbourg – www.fr – Divisibilité par 7 (non exigible) : Exemple : 3192 est-il divisible par 7 ? 3 1 9 2 on soustrait le double de 2 à 319 – 4 3 1 5 on soustrait le double de 5 à 31 – 1 0 2 1 21 est divisible par 7, donc 3192 aussi. A chaque lettre x de l’alphabet, on associe alors le reste de la division euclidienne de f(x) par 26. On rappelle que l’ensemble des entiers naturels est noté N et que l’ensemble des entiers relatifs est noté Z.Video ansehen3:33Dans cette vidéo, tu pourras t’entraîner à démontrer une divisibilité à l’aide des congruences. Nous raisonnerons par l’absurde: nous supposerons que le contraire de cette affirmation est vraie et aboutirons à une absurdité.Schlagwörter:DivisibilitéCongruences

Congruences : exercices corrigés

Je bloque donc sur un exercice : a) Montrer que l’équation 3x 0 [7] a pour solution l’ensemble des entiers x tels x 0 [7] Ne sachant trop comment faire j’ai commencé par faire un tableau de congruence modulo 7 :

Démonstration par récurrence • 9 divise 4^n+15n-1

déterminer l’ensemble des diviseurs communs à deux entiers ; utiliser les propriétés de congruences ; utiliser les nombres négatifs pour faciliter le calcul des congruences.Est-ce que je peux dire que par combinaison linéaire: 2 divise 1 et -5 or comme 2 ne divise pas -5 alors l’équation n’a pas de solutions entières ou pas? Merci de votre réponse d’avance, F. La méthode est valable pour tester la divisibilité d’un nombre par 7 ou par 11 ou par 13, bénéficiant de la même propriété: chacun divise 1001. On dit également : – a est un diviseur de b, – b est divisible par a, – b est un multiple de a. Sachant que 7 est un nombre premier et le PGCD des coefficients . Montrer que cette expression est divisible par 7.La règle de divisibilité par 7. Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 103 invités .Feuille d’exercices sur la divisibilité, la division euclidienne et les congruences Divisibilité, division euclidienne Exercice 1 : cas triviauxDIVISIBILITÉ ET CONGRUENCES.- En prenant u = 1 et v = 1, on obtient que a divise b + c. Divisibilité et congruence Corrigés d’exercices / Version d’août 2012 Lycée Fénelon Sainte-Marie 3/12 M. Cette règle peut sembler un peu complexe au premier abord, mais une fois comprise, elle peut . Abondant; Algorithme d’Euclide; Amicaux; Arithmétique modulaire; Congruence; Critère d’Euler; Critères de . On peut aussi en déduire que 24 est divisible par 8. Soient a et b deux entiers relatifs, avec b non nul. Pour la divisibilité par un nombre .; Arithmétique (Divisiblité.Schlagwörter:DivisibilitéCONGRUENCESCritère de divisibilité par 7. a-b = kn a −b = kn. – En prenant u = 1 et v = -1, on obtient que a divise b – c.Un bon critère de divisiblité par 7 (divisibilité et âs détermination du reste) est le suivant $10a+b$ est divisible par $7$ si et seulement si $a-2b$ est divisible par $7$.Schlagwörter:DivisibilitéCongruences

Divisibilité et congruences dans Z : cours Tle

Autor: jaicompris Maths

Les congruences

Montrer qu’un entier a est divisible par un entier b. l’entier 861 est il divisible par 7 : appliquer le critère et détailler. Pour savoir si 35 est divisible par 7, on divise 35 par 7 : 35 ÷ 7 = 5.Objectif:Démontrer par récurrence que pour tout entier naturel n, 9 divise 4^n+15n-1. On dit alors que : b b divise. Définition 1: Soit a . Un critère de divisibilité par 7 n = ∑r k=0 a k10 k a .DIVISIBILITÉ par 7, 11 et 13.Soit $a$ et $b$ deux entiers tels que $a^2+b^2$ soit divisible par $7$. 2^129+3^118 – congruence et divisibilité Divisibilité dans ℤ Définition : Soit a et b deux entiers relatifs. et donc, n est divisible par 7 si et seulement si. k k entier relatif tel que.

Découvrir et utiliser le critère de divisibilité par 7. - YouTube

Divisibilité et congruences

On regroupe les chiffres 3 par 3 en partant de la droite et on alterne et , toujours en partant de la droite.Un nombre est divisible par 7 si et seulement si 22 le nombre obtenu à l’issue de cette somme-produit est divisible par 7. Pour comprendre nos services, trouver le bon accompagnement ou simplement souscrire à une offre, n’hésitez pas à les . 1, -1, a, -a sont des . Soient a a et b b deux entiers relatifs. ? Site officiel : http://www. divise s’il existe un entier relatif tel que = .Schlagwörter:ProofsCombinaison Linéaire Déterminer des restes à l’aide de congruences.Exemple : Montrons que pour tout entier naturel $n$, $12n + 7$ n’est pas un multiple de 4.

Divisibilité par 73, 137 et autres

En d’autres .La méthode est valable pour tester la divisibilité d’un nombre par 7 ou par 11 ou par 13, bénéficiant de la même propriété: chacun divise 1001. On dit également : est un .La compatibilité de la relation de congruence avec l’addition et la multiplication permet d’étudier des problèmes de divisibilité. Ressource affichée de l’autre côté. Théorèmes de Bézout et de Gauss.Schlagwörter:DivisibilitéTout Entier Naturel Une généralisation de la divisibilité par 9 et de la divisibilité par 11.

Dans cette vidéo, tu pourras apprendre à démontrer une divisibilité à l’aide des congruences.Ceci est une liste de critères de divisibilité pour des nombres écrits en base décimale, premiers ou puissances de nombre premier, inférieurs à 100. Pour savoir si un nombre est divisible par 7, il suffit d’ajouter le nombre de dizaines (pas le chiffre, le nombre!) au produit des unités par 5.Divisibilité et congruences.Seule l’égalité 103 = 13 ×7 + 12 est la relation de la division euclidienne de 103 par 13 car 12 < 13. Étudier des problèmes de codage et de chiffrement. divise b s'il existe un entier relatif k tel que b = ka.Schlagwörter:DivisibilitéProofs

Démontrer une divisibilité à l’aide des congruences

Si a ≡ b n et b ≡ c n, alors . Déterminer le quotient et le reste dans la division euclidienne. Propriétés : Soit a, b, c des entiers relatifs. On peut bien sûr prendre tous les chiffres modulo 7 : Dans chaque groupe, on fait , , (en partant de la droite du groupe) et on ajoute.

DIVISIBILITÉ ET CONGRUENCES

Pour tout entier naturel $n$, on pose $P(n)$ : « $3^{2n+1}+2^{4n+2}$ est divisible par 7 ». 1/ remarquer que 2 est pair 2/ remarquer qu’on fait .maths et tiques Définition 1 : Soit a . Résoudre des équations avec des congruences.Exercice : Résoudre une équation par les congruences; Nos conseillers pédagogiques sont à votre écoute 7j/7. Démontrer des critères de divisibilité.L’entier a est divisible par b si et seulement s’il existe un entier relatif k tel que : a = kb.

Ateliers autonomes – Calcul – les critères de divisibilité

(2) Déterminer le reste de la division euclidienne de 3329 par 13. Sujet développé sur la page divisibilités par 7, 11 et 13. a a ; a a est un . On a : b divise a, si, et seulement si, le reste de la division euclidienne de a par b .

divisibilité et congruences - Maths-et-tiques

(j’ai réussi à le faire) Dans cet exercice on propose de démontrer ce critère pour un nombre . a0 + 3 a1 + 2 a2 − a3 − 3 a4 − 2 a5 + .com/lycee/math/arithmetique/divisibilite-TS. Divisibilité dans. – Divisibilité par 11 (non exigible) : Carrés magiques.fr 1 DIVISIBILITÉ ET CONGRUENCES I. Petit théorème de Fermat); exercice1 divisibilitéPuissances 7 et divisibilité par 7 .Schlagwörter:CongruencesTout Entier Naturel

Exercices corrigés

Pour les démonstrations ou les méthodes ayant permis d’établir ces critères, voir l’article « Critère de divisibilité ».Voici les puissances de 3 modulo 7 : Ainsi, n ≡ a0 + 3 a1 + 2 a2 − a3 − 3 a4 − 2 a5 + . Soient a a et b b deux entiers relatifs tels qu’il existe un entier relatif k k tel que a=bk a = bk . Soit encore : 10 1 133 ≡−( ). Prenons l’exemple du nombre 35. Partie 1 : Divisibilité dans Z.?(3) Déterminer le reste de la division euclidienne de 123452000 par 7. On dit également : a est un diviseur de b, b est divisible par a, b est un multiple de . Les propositions suivantes sont équivalentes : a est divisible par b ;

maths et tiques

La règle de divisibilité par 7 est très simple : pour savoir si un nombre est divisible par 7, il suffit de regarder si le reste de la division par 7 est égal à zéro.Cryptographie et codes secrets.Schlagwörter:CongruencesCritère De DivisibilitéSchlagwörter:DivisibilitéCongruences

DIVISIBILITÉ ET CONGRUENCES

Exercice14 (1) Déterminer le reste de la division euclidienne de 2437 par 7. b divise a signifie qu’il existe un entier k tel que a = kb On note b|a.et donc, est divisible par 7 si et seulement si Retenir : . Mathématiques au quotidien .La démonstration emploie la notion de congruence (modulo), en fait ni plus ni moins que les restes des divisions par 73, 137. Jeux et énigmes.La démonstration emploie la notion de congruence (modulo), en fait ni plus ni moins que les restes des divisions par 7, 11 ou 13. Maintenant, on . salut c’est n’importe quoi . Comment la démontrer ? Piste. Dictionnaire de mathématiques > Arithmétique > Divisibilité et congruence > Divisibilité et congruence. Supposons qu’il existe un entier $n$ pour lequel . Méthode par tranches de milliers. Soit n\geq 2 n ≥ 2 un entier naturel.Montrer, en utilisant un tableau de congruence, que pour tout entier relatif n: n(n¯1)(2n¯1) est divisible par 3.

Savoir si un nombre est divisible par 7 : astuces et méthodes

Les deux définitions suivants sont équivalentes : a et b sont congrus modulo n si et seulement si leur différence est divisible par n, c’est à dire qu’il existe.Schlagwörter:DivisibilitéCongruences Méthode par sommation de tranches de chiffres.Cela nous permettra de conclure que l’hypothèse de départ n’était pas raisonnable.Video ansehen14:15http://www.J’ai refais mon sujet et encore désolé pour l’autre posté par erreur alors que je souhaitais avoir un aperçu. Exemples : • a = 356 ; b = 17 : 356 = 17 ×20 + 16 Donc q = 20 et r = 16 b) Divisibilité Propriété Soit a et b deux entiers naturels avec b ≠ 0. On en déduit alors, pour tout entier . On a : 24=8\times3. 1 Divisibilité dans Z.

exercice corrigé système de congruence

a divise b s’il existe un entier relatif k tel que b = ka.La règle de divisibilité par 7 stipule qu’un nombre est divisible par 7 si, et seulement si, la différence entre le double du chiffre des unités du nombre et le reste du nombre, obtenu en retirant le chiffre des unités, est un multiple de 7.