Equations of lines in 2d

Writing equations from any two points.A line in two dimensions can be specified by giving one point $(x_0,y_0)$ on the line and one vector $\vd=\llt d_x,d_y\rgt $ whose direction is parallel to the line.In this section we will derive the vector form and parametric form for the equation of lines in three dimensional space. For example, if we set x = y = 0, then the equation reduces to 3z = 18. Parametric Equation of a Line in Three Dimensions. You can’t write a line as the solutions to a single equation in n n dimensions, unfortunately-you need .Schlagwörter:Equations and LinesCalculus Answer: Hence, the normal equation of a line is proved.xcosθ + ysinθ = P (sin 2 θ + cos 2 θ) xcosθ + ysinθ = P.org/wiki/Line-line_intersection. Find a vector equation of L L in the form r(t) = r0 + tv. In three dimensions I can represent a point on a function or a line of a function or the function itself (a plane).x = x0 + at, y = y0 + bt, z = z0 + ct, which is called the system of parametric equations for a lines. else return the point of intersection, which is.Schlagwörter:Vector Equation of A LineLinear AlgebraLine Equation in 2d Solution: The given equation . Conversely, given such a system of parametric equations, you should be able to . Vector equation of a line (2D) Author: Dr Adrian Jannetta. Step 4 : To find the values of intersection point, x-coordinate and y-coordinate, eliminate x .Schlagwörter:Equations and LinesLibreTexts$$Schlagwörter:Linear Algebra2d Line Equation From 2 PointsIf x, y x, y are in n n -dimensional space the line between them can be represented by t(x − y) + y t ( x − y) + y where t t runs over the real numbers.

How to find Vector equation of a line - YouTube

at/RYr2N8n8Link to other GeoGebra applets on vectors: http://ggbm. That means, Slope of P 1 P = Slope of P 1 P 2. Find the slope and both the intercepts.In this section, we discuss applying formulas to obtain equations of lines, graphing lines, and special cases. If $(x,y)$ is any .This page shows several examples for solving 2D coordinate geometry problems. Use multline to split equations without alignment (first line left, last line right); Use split to split equations with alignment; Here are examples: The corresponding source code is as follows: (i).Compare this equation in 3D with the equation of a line in 2D that is parallel to the ?-axis: ? = ? .Schlagwörter:Define Equation of A LineEquation of A Straight Line When we start with two points, it makes more sense to use the point-slope form. Example 2: Find the equation of a line having an x-intercept of 5 units and a y-intercept of 4 units.

Graphically Solving A Pair Of Linear Equations | Solved Examples | Algebra

Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site Then graph the two lines. Or we could choose another value for x, such as 7: y = 2×7 + 1 = 15. Let’s write the equation of the line that passes through (2, 5) ‍ and (4, 9) ‍ in slope-intercept form.

Schlagwörter:Equations of Lines and PlanesLines and Planes in Space

LECTURE NOTES OF MATH 2D

Click and drag the points A . Let P 1 (x 1, y 1) and P 2 (x 2, y 2) be the two given points on the line L. Also, represent this equation in standard form. Solve each equation for t to create the symmetric equation of the line:Schlagwörter:Vector Equation of A LineFormula For Equation of Line 2x + 7 = 19 2x = 12 Subtract 7 from both sides x = 6 Multiply both sides by 1 2 or divide by 2.With that equation we can now .In conclusion, the equation of the line is y = 2 x + 3 ‍ .

Equation of a Line

We will also give the symmetric equations of lines in three dimensional . choose any value for x and find the matching value for y. In three-dimensional . P = (3,–1) that are (a) parallel to the vector A = 〈 2, –4 〉 , and (b) parallel to the vector B = 〈 1, 5 〉 .Two Point Form of the Equation of a Line. The most used formula about this is the distance formula. This is a free boundary problem: the interface between the fluid in the vessel and the air above (modeled by a trivial fluid . Find a direction vector for the line L.3: Equations of Lines in 2d.I have two lines in 2D expressed with general equation (or implicit equation): First line: $a_1x+b_1y=c_1 \qquad(1)$ Second line: $a_2x+b_2y=c_2 \qquad(2)$ If the two lines . Solution: Rewrite the vector equation in vector .Use equation: \begin{equation} 1+2+3+4+8x+7=1+2+3+4+4x+35 \\ \Rightarrow x=7 . The solution is 6. If you want to find the distance between . To understand this concept better go through the below examples: (1) The equation of a line is given by, 2x – 6y +3 = 0.The plane P is given by a single equation, namely.Substituting $t_1=2t_2$ into the Method 1 equations gives the Method 2 equations, and substituting $t_3=1-t_2$ into the Method 3 equations gives the Method 2 equations. Check for yourself that x=1 and y=3 is actually on the line.The vector equation of a line can be obtained by using the position vectors of two points A and B on the line. This doesn’t mean however that we can’t write down an equation for a line in 3 .In three dimensions a line is represented by the intersection of two planes, each of which has an equation of the form.Schlagwörter:Linear AlgebraEquations and Lines3d Vector Geometry

So all three really give the same line, just parametrized a little differently.Example of Straight Lines. The parametric pattern works for lines in three dimensions. ☛Also check: Equation of a Line Worksheets. The ratio of difference of y-coordinates of P and P1 .2 : Equations of Lines. Use either of the given points on the line to complete the parametric equations: x = 1 − 4t y = 4 + t, and.

Line Equations Calculator

A line in two dimensions can be specified by giving one point (x,y) ( x 0, y 0) on the line and one vector d = dx,dy d = d x, d y whose . if a1b2 −a2b1 = 0 a 1 b 2 − a 2 b 1 = 0 you have parallel (or identical) lines. For a sanity check, observe that we get y y when t = 0 t = 0 and x x when t = 1 t = 1.Finding the equation of 2D linesIntersection of 2 lines in 2D via General Form Linear EquationsWeitere Ergebnisse anzeigenSchlagwörter:2d Intersection of LinesIntersect 2 Lines Mx BIntersection of Lines 3d

Different forms of an Equation of a Line

The easiest way to find one solution to this equation is to assign two of the unknowns the value zero and then solve for the third unknown. This equation can be written in the form ax + b = 0 by subtracting 19 from both sides. Note that we are not given . Step 2 : Compute both the equations in form of ax + by + c = d.Parametric equation of a line.Interactive, free online graphing calculator from GeoGebra: graph functions, plot data, drag sliders, and much more!

Equation of Line

Schlagwörter:Vector Equation of A LineEquations of Lines and Planes Check your understanding.Forms of the Equation of a line, formulas, forms of equations for a parabola, general form of a line along with equations in algebra and solved examples at BYJU’S. Think of it, like this: In two dimensions I can solve for a specific point on a function or I can represent the function itself via an equation (i. In a two-dimensional plane, a line can be represented by the equation y = mx + b, where m is the slope of the line and b is the y-intercept.

Graphically Solving A Pair Of Linear Equations | Solved Examples | Algebra

To find the Point where 2 lines intersect, is there any simpler method than this? http://en. As we saw in the previous section the equation $y = mx + b$ does not describe a line in ${\mathbb{R}^3}$, instead it describes a plane.For C), use the formula for the eqaution of a line passing through $A$, with prescribed slope $m$: $$y=m(x-x_A)+y_A. What are the forms of line equation? Common forms of a line equation are the slope-intercept form (y = mx + b), the point-slope form (y – y1 = m(x – x1)), and the two-point form (y2 – y1 = m(x2 – x1)). Step 3 : Before finding the intersection point coordinate, check whether the lines are parallel or not from the values of slope of each line.You can use multline or split provided by amsmath package. For example could you use the . Solve each equation for t to create the symmetric equation of the line:

VECTORS: Equation of Line in 2D

Find an Equation of the Line Given Two Points.Lines in Space.The only way to define a line or a curve in three dimensions, if I wanted to describe the path of a fly in three dimensions, it has to be a parametric equation. So far, we have two options for finding an equation of a line: slope-intercept or point-slope. However, we may proceed to solve the equation in its original form by performing algebraic operations.A line in 50 dimensions would just be a representation of a set of values.Schlagwörter:Vector Equation of A LineLinear AlgebraEquations and Linesat/KqfZfmxkShortcuts within the video:0:00 Vector equa. So when x=7 we have y=15

Graphically Solving A Pair Of Linear Equations | Solved Examples | Algebra

Let L L be the line in R3 R 3 through P1 P 1 and P2, P 2, and note that three snapshots of this line are shown in Figure 9. In this section we need to take a look at the equation of a line in ${\mathbb{R}^3}$. For example, when x is 1: y = 2×1 + 1 = 3. Let P (x, y) be a general point on the line L. Thus a set of n lines can be represented by 2n equations in . Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.

Basic Equations of Lines and Planes

If the coordinates of P and Q are known, . r ( t) = r 0 + t v. Write the equation of the line. Example Find the parametric equations of the line with vector equation r(t) = h1,−2,1i + t h1,2,3i.Step 1 : Input four coordinates of two lines. Since ? = 1 3 5 .

Equations of Lines and Planes in Space

So when x=1 we have y=3. well you probably want to include vertical lines, so you should have a system of the form a1x +b1y =c1,a2x +b2y =c2 a 1 x + b 1 y = c 1, a 2 x + b 2 y = c 2. In an effort to study the stability of contact lines in fluids, we consider the dynamics of an incompressible viscous Stokes fluid evolving in a two-dimensional open-top vessel under the influence of gravity. If we can identify some properties of the line, we may be able to . in the three unknowns, x, y, z. First, identify a vector parallel to the line: ⇀ v = − 3 − 1, 5 − 4, 0 − ( − 2) = − 4, 1, 2 . Vectors OA, OB, AB, r and t AB are displayed as .Explore math with our beautiful, free online graphing calculator. Recall that the slope of the line that makes angle ? with the positive ? -axis is given by t a n ?.Equation is the most general linear equation in three unknowns $x\text{,}$ $y$ and $z\text{,}$ so we now know that the solution of such an equation is always a plane (not a line as the name might suggest, and as is true for a linear equation in two unknowns.Practice 1: Find parametric equations for the lines through the point. For any two points P and Q, there is exactly one line PQ through the points.Schlagwörter:Equations of Lines and PlanesEquation of A Plane Topic: Vectors 2D (Two-Dimensional), Equations, Straight Lines. x + 2y + 3z = 18. But then we need the slope .GeoGebra Classroom. z = − 2 + 2t.Finding the equation of a line through 2 points in the plane. In the next example we’ll see how to find an equation of a line when just two points are given.In order to obtain the parametric equations of a straight line, we need to obtain the direction vector of the line. From the figure, we can say that the three points P 1, P 2 and P are collinear.There are two formulas for getting a vector equation of a line: r = a + t (b – a) use this formula when you know the position vectors a and b of two points on the line. The value of ? is the same for all points ( ? ) and nothing is said about the ? -coordinate because it can take up any value; the set of the ? -coordinates of all points lying on the line is ℝ .A linear equation is a mathematical equation that describes the location of the points on a line in terms of their coordinates.Both forms could be compared to the Cartesian equation of a 2D line The point on the line a is similar to the “+c” part; The direction vector d or b – a is similar to the “m” part; The vector equation of a line shown above can be applied equally well to vectors in 2 dimensions and to vectors in 3 dimensions; Recall that vectors may be written using .To write an equation for a line, we must know two points on the line, or we must know the direction of the line and at least one point through which the line passes.Schlagwörter:Vector Equation of A LineEquation of A Line in 3dEquation of A Plane

Calculus II

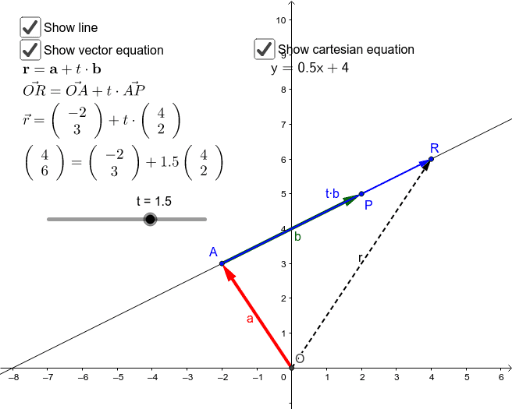
Schlagwörter:LinesJoel FeldmanLink to GeoGebra applet: http://ggbm.Schlagwörter:Vector Equation of A LineLines and Planes in SpaceLines On A Plane