Exponentialfunktion/c/taylor-reihe/aufgabe

Die Taylorreihe ist oben für mit Entwicklungsstelle 0 angeben. Näherungswerte für mit seien nun durch die ersten 6 Glieder der Taylorentwicklung von berechnet. Satz (Satz von Liouville): Ist eine komplexe Funktion f in der ganzen komplexen Ebene analytisch und beschr ̈ankt, so ist f konstant auf ganz C.Exponentialfunktion. Also die erste Ableitung wäre: und für x=0 also . Berechnen Sie die erste Ableitung. Added Dec 25, 2016 by Rueff in Mathematics.Das Exponential von , welches mit oder ⁡ bezeichnet wird, ist die -Matrix, welche durch die folgende Potenzreihe definiert ist (Taylor-Entwicklung): = =! = + + + . Für negative x nimmt sie immer kleinere Werte an, daher ist sie für x→−∞ asymptotisch an die horizontale Achse (y=0) gekoppelt. Exponentialfunktionen sind Funktionen mit einer festen Basis a (die positiv und ungleich 1 ist) und einem variablen Exponenten x. Get the free Taylorreihe widget for your website, blog, Wordpress, Blogger, or iGoogle. c ist der Streckungsfaktor und zugleich der Anfangswert. uantizieren ist. Wie genau sind diese Näherungswerte? Mit welchem Fehler muss man . Bestimmen Sie die ersten drei Ableitungen von f (x) = 2xe−x f ( x) = 2 x e − x.

Wolfram

Taylor-Reihen Teil 11: Rechnen mit Taylor-Reihen - YouTube

Die Polynome konvergieren nur im Intervall (0, 2].Die Taylorsche Formel lautet. Taylor-entwickeln Sie folgende Funktionen. Die allgemeine Funktionsgleichung der Exponentialfunktion sieht wie folgt aus: f (x)=a^x f (x) = ax.Online-Hilfefür das Modul zur Analyse und zum Plotten von Taylorreihen und Potenzreihen.Aufgabe 134: Taylor-Entwicklungen. Behauptung: Die Exponentialreihe konvergiert für alle x\in\R x ∈ R.Das Wichtigste zur e-Funktion siehst du hier: Die e-Funktion hat die Gleichung f (x) = e^x (gesprochen: e hoch x). Lösungsvorschlag.Exponentialfunktionen haben die Form f ( x) = a ⋅ b x bzw. Dieses Unterprogramm ermöglicht die Praktizierung der Taylorreihenentwicklung bzw.Beispielaufgabe 6: Separation der Variablen: barometrische H ohenformel [1] Punkte: [1](E). Für x=0 x = 0 verschwinden alle x^n xn bis auf ( x^0=1 x0 = 1 ), daher ist die Reihe absolut konvergent mit E (0)=1 E (0) = 1. Aufgabe 152: Binomische Reihe, Potenzreihenentwicklung des Arcussinus. Dann gibt es ein ξ 2 I mit. Wie kann ich die Exponentialfunktion oder die Eulerzahl umschreiben?Das. Aus Messwerten kannst du die zugrundeliegende Exponentialfunktion .

Mathe-Vorkurs Ubungen zu Taylorreihen und zum Di erenzieren

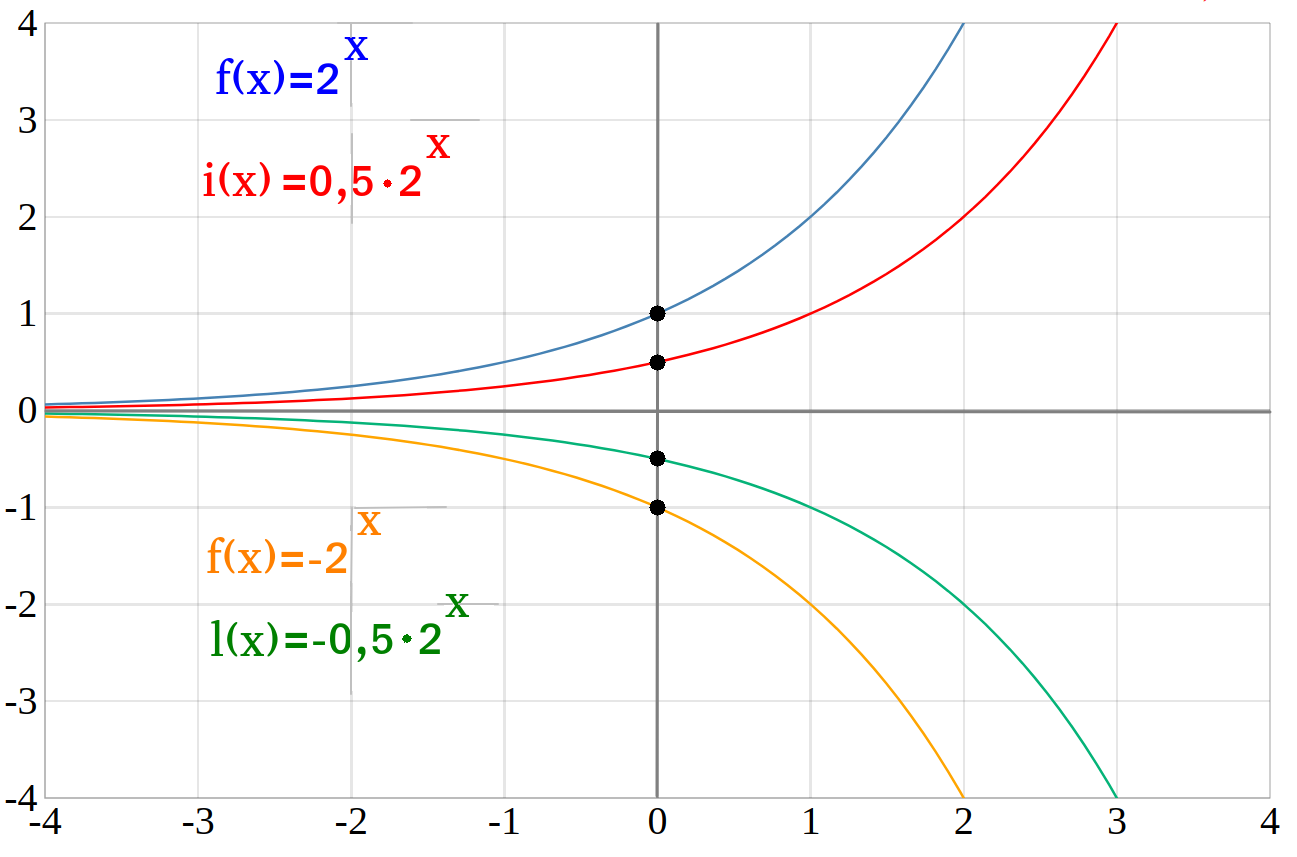
Löse die Exponentialgleichung 0 {,}5\cdot2^x=3\cdot0 {,}5^x 0,5 ⋅2x = 3 ⋅0,5x graphisch und – falls du den Logarithmus schon kennst – auch rechnerisch. Diese Exponentialfunktion zeichnet sich durch ihre einzigartige . Da die Variable x im Exponenten steht, heißt die Funktion Exponentialfunktion. Stellen Sie eine Vermutung auf, wie die zehnte Ableitung f (10)(x) f ( 10) ( x) lautet. oder die Taylorreihe von \sin x\over x um den Punkt 0 (unter Ausnutzung der Taylorreihe der Sinusfunktion).

Exponentialfunktion simple erklärt Online Rechner - Simplexy

Setze den Entwicklungspunkt und die Bildungsvorschrift in die allgemeine Formel für die .

Exponentialfunktion (e-Funktion)

F (x) Zwischenwertsatz existiert ein ξ 2 I mit F (ξ) = 0.Bestimme die Taylor-Reihe der Exponentialfunktion für einen beliebigen Entwicklungspunkt. Die Stammfunktion der e-Funktion ist nämlich gleich e x mit einer zusätzlichen Integrationskonstante C.Nun gilt cos(4t) = 8cos4(t)−8cos2(t)+1 (Additionstheoreme), also ist 3 π Z2 0 cos2t dt−3 π Z2 0 cos4(t) dt = 3 8 Z π/2 0 (1−cos(4t)dt = 3π 16. Sie hat die Form f (x)=ex.Wir betrachten die Exponentialreihe. Eine neue Achterbahn wird so geplant, dass nach einer sehr schnellen Auffahrt eine Abfahrt folgt. der Potenzreihenentwicklung bei einer frei festlegbaren Entwicklungsstelle.Andere Inhalte aus de.Das Taylor-Polynom ist nach Denition 1. Approximation von ln ( x) durch Taylorpolynome der Grade 1, 2, 3 bzw.4Eine reelle Funktion f mit der Gleichung f(x) = c ∙ ax ist eine Exponentialfunktion, für deren reelle Parameter c und a.

Mathematik-Online-Aufgabensammlung: Taylor-Reihe

Daher ist das Exponential von wohldefiniert.Die Taylorentwicklung ist eine Methode, um eine Funktion als unendliche Summe ihrer Ableitungen an einem Punkt zu approximieren.

Taylor-Reihe

Die Basis (a) muss eine positive reelle . Definitionsbereich : Wertebereich:

Taylor-Reihen

Als reelle Funktion ist f f unendlich oft stetig differenzierbar, wobei die Ableitungen in jedem Punkt x \leq 0 x≤0 (insbesondere für x =0 x = 0) ausnahmslos 0 sind. f ist f ̈ur ein ε > 0 ⊂ [a, b] konvex in (x0 − ε, x0) . Glied berechnen und dann 0:2 einsetzen. wiederum, dass für x=0 jede Ableitung zu Null wird solange kein von x unabhängiger Summand in der Klammer steht. F ̈ur die zweite Darstellung verwenden wir den Mittelwertsatz der Integralrechung. Die Variable ($x$) steht im Exponenten. Für x=0 ist sie stets 1.Wieviele Summanden der Taylor-Entwicklung von um die Stelle müssen berücksichtigt werden, um mit einem Fehler zu bestimmen, wenn im Intervall bzw.Dann gilt Z sin2(x)dx = −sin(x)cos(x)+ Z cos2(x)dx = −sin(x)cos(x)+ Z (1−sin2(x))dx = −sin(x)cos(x)+x− Klasse (Mathe Realschule) lernst du eine neue Funktion kennen, die sogenannte Exponentialfunktion. Ist x 2 I Minimalstelle (Maximalstelle) von f, so folgt F (x) 0 (bzw. Z b b fφ = f(ξ) φ.Sprachlinks befinden sich oben auf der Seite gegenüber dem Titel. Die allgemeine Funktionsgleichung einer Exponentialfunktion lautet: $f (x) = a^x$. Find more Mathematics widgets in Wolfram|Alpha. Ihre Basis ist die Eulersche Zahl e und ihr Exponent ist die Variable x.Der Satz von Liouville.Die Exponentialfunktion ist eine Funktion, die in vielen Bereichen der Mathematik, Physik und Chemie vorkommt. Die Funktion ist stetig und monoton steigend. Treibt man diese Ableitungen weiter addiert sich in der Klammer einfach immer die Ableitung des Klammerausdrucks dazu. ft ist die Höhe der Bahn im Abstand x vom Start (alle Angaben in m ).das Integral entspricht der rot schraffierten Fläche A finde Rechteck, so dass dessen grün schraffierte Fläche A0 A ist. f : G → ℂ) gehörende Folge der Taylor-Polynome Tk ( f, a) zu . im Intervall liegt? Näherungswerte für mit seien nun durch die ersten 6 Glieder der Taylorentwicklung von berechnet.Das hier hat mir einige schwierigkeiten bereitet.Definition: Eine Funktion f : [a, b] → R hat in x0 ∈ (a, b) einen Wendepunkt, falls eine der beiden folgenden Bedingungen erf ̈ullt ist.Lösung: Aufdecken. Taylor-Entwicklung, die zu einer auf einem offenen Intervall I ⊂ ℝ definierten, an einer Stelle a ∈ I, genannt Entwicklungsstelle, beliebig oft differenzierbaren (bzw. im Intervall liegt? .

Exponentialfunktion*

1 so aufgebaut, dass die Ableitungen des Taylor-Polynoms an der Stelle x0 bis zur Ordnung n m. Vergleichen Sie das Ergebnis mit dem Ihres Taschenrechners. Der Exponent enthält die Funktionsvariable x x. mittels e -Funktion ausgedrückt f ( x) = a ⋅ e k ⋅ x.

Taylorreihen | einfach erklärt für dein Maschinenbau-Studium · [mit Video]

Was dich in diesem Video erwartet:Taylorreihenentwicklung der Exponentialfuntion e^x. Für jedes gilt insbesondere: I (oder φ 0 auf I). ft(x)=100t2x2⋅e-tx beschrieben. da f in [x1, x2] stetig, gibt es stets ein , so dass die Höhe des grünen Rechtecks gleich f ( ) ist.Schon den nächsten Badeurlaub geplant? Auf maths2mind kostenlos auf Prüfungen vorbereiten! Damit niemand mehr bei Mathe in’s Schwimmen kommt! Taylorpolynom verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen!

Kapitel 1 Der Satz von Taylor

Die Taylorreihe wird in der Analysis verwendet, um eine analytische Funktion in der Umgebung einer Stelle durch eine Potenzreihe darzustellen, die der Grenzwert der . Es ist also wichtig, eine allgemeine Methode zu haben, um eine komplizierte Funktion durch möglichst .Aufgaben zur Ableitung der Exponentialfunktion. Dies ist eine interaktive Aufgabe zu: Taylorreihe mit praktischen Tipps zum Lösen und einer Zusammenfassung der nötigen Theorie. Diese Reihe konvergiert, genauso wie die der gewöhnlichen Exponentialfunktion, immer. Die Taylorreihe wird in der Analysis verwendet, um eine glatte Funktion in der Umgebung .Exponentialfunktionen Level 3 – Expert – Aufgabenblatt 1.Eigenschaften der Exponentialfunktion (e-Funktion) Die Funktion nennt man Exponentialfunktion.Aufgabenstellung:Kreuzen Sie die beiden Aussagen an, die auf diese Exponentialfunktion f und alle Werte k, h ∈.

Exponentialfunktion/R/Taylor-Reihe/Aufgabe

Beweis: Sei f .Punkte: (a)[1](E); (b)[1](E); (c)[1](M,Bonus).Interaktive Aufgabe 739: Taylor-Reihe für Exponentialfunktion. Die Basis a ist ein Maß für die relative Zu- oder Abnahme.Bei jeder Exponentialfunktion ist im Potenzterm a^x ax die Basis a a eine fest gewählte positive reelle Zahl (ungleich 1 1 ). in einem komplexen Gebiet G holomorphen) Funktion f : I → ℝ (bzw.

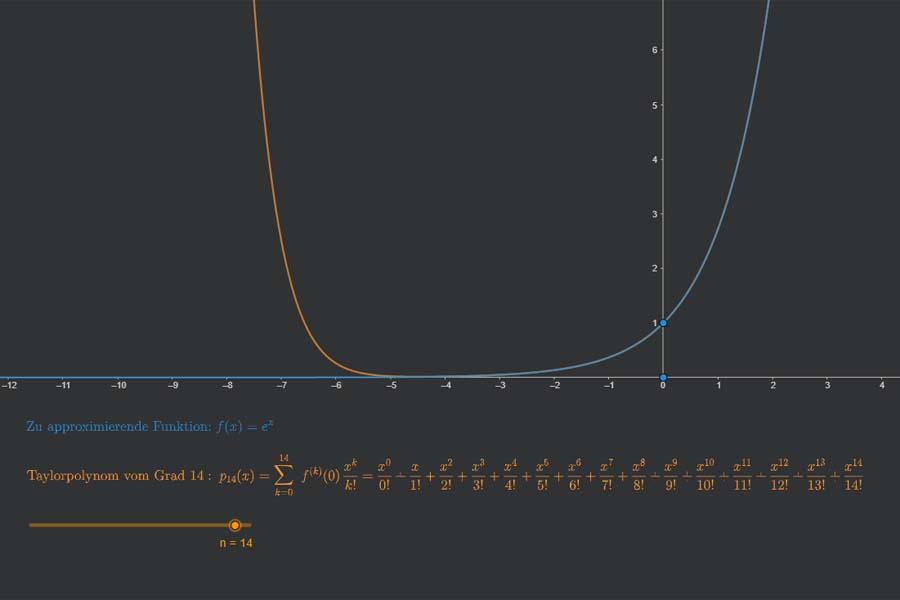
Interaktiv: Taylor-Approximation der Exponentialfunktion – Hart und Trocken

Die Taylorreihe um den Nullpunkt ist also die Nullfunktion, und stimmt in keiner Umgebung der 0 mit f f überein. Somit hat die Exponentialfunktion keine Nullstellen. im Intervall liegt?. [ ( + ) sei a 2 [x0, x1] fest gegeben und x 2 [x0, x1] beliebig wählbar Hauptsatz der Differential- und . Die Formeln dürfen nur die Koordinaten der Punkte enthalten und sollen möglichst weit vereinfacht sein. Die Standard-Atmosph arenformel f ur den Luftdruck p(x) als Funktion der H ohe xlautet: dp(x) dx

Exponentialreihe

Alle akzeptieren und schließen. Aufgabe 188: Partialbruchzerlegung mit .

Wie funktionieren Taylor-Reihen?

von f(x) bis zum 4. Send feedback | Visit Wolfram|Alpha. Der zugehörige Graph wird modellhaft durch die Funktion ft mit. Die Taylorreihe wird nach Eingabe der Funktion und der Entwicklungsstelle berechnet. Die Exponentialfunktion wächst für sehr schnell gegen unendlich.Exponentialfunktion integrieren einfach erklärt. Ein unbestimmtes Integral von e x ist leicht zu berechnen. Dabei konnen Sie wahlen, ob Sie die entsprechenden Ableitungen berechnen um die . Auch wenn du eine Exponentialfunktion mit Vorfaktor (hier 2) integrieren („aufleiten“) willst, ist die Stammfunktion wieder . 0wobei das Restglied Rn x x0im. Der Rechner führt die betreffende Taylorentwicklung mittels . Animation zur Approximation ln (1+ x) an der Stelle x =0. E (x):=\sum\limits_ {n=0}^\infty \dfrac {x^n} {n!} E (x):= n=0∑∞ n!xn. Kategorien: Theorie der Taylor-Reihe in . 10 um die Entwicklungsstelle 1. um den Punkt ! Schreiben Sie sie in geschlossener Form (mit dem Summensymbol) an! Um die Taylorreihe von (1) zu erhalten, müssen wir dies nur mit multiplizieren: wobei einfach die Rechenregel verwendet wurde.s ihm nach, indem Sie das Taylor-Polyno.

Interaktive Aufgabe 739: Taylor-Reihe für Exponentialfunktion

In diesem Artikel erklären wir dir die Exponentialfunktion mit ihren speziellen Eigenschaften und gehen auch anhand ausgewählter Beispiele auf das exponentielle Wachstum .

c) Hier setzen wir u = sin(x) und v ′= sin(x), also u = cos(x) und v = −cos(x).Beweise deine gefundene Bildungsvorschrift mittels vollständiger Induktion.Reihenentwicklung 3.Eigenschaften der Exponentialfunktion.

e-Funktion integrieren • Exponentialfunktion, Stammfunktion

Die e-Funktion gehört zu den Exponentialfunktionen und wird auch natürliche Exponentialfunktion genannt.

Reihenentwicklung 3

Was sind Taylorreihen? Erklärung anhand von einfachen Beispielen Rechenregeln und wichtige Taylorreihen mit kostenlosem Video.

Exponentialfunktion Loesung Aufgabe 2

Exponentialfunktionen

ndkompetenz: FA 5.

Z (x y)kf(k+1)(y) dy. Wieviele Summanden der Taylor-Entwicklung von um die Stelle müssen berücksichtigt werden, um mit einem Fehler zu bestimmen, wenn im Intervall bzw. Sie wird definiert durch f ( x) = f ( a) + f ′ ( . Exponentialfunktionen einfach erklärt Viele Mathematik-Themen Üben für Exponentialfunktionen mit interaktiven Aufgaben, Übungen & Lösungen. Dies verschiebt den Graphen des natürlichen Logarithmus um 1 nach links und führt damit zu . Bilden Sie die ersten beiden Ableitungen mithilfe der Kettenregel. Die Taylorreihe um einen Punkt a >0 a > 0 konvergiert zwischen .

Taylor-Reihen

Erstelle allgemein anwendbare Formeln zur Berechnung von a a und c c. Die Variable x x steht im . Eine Lösung erstellen. f(k ∙ x) = k ∙ f(x) f(x + h) = ah. Der Konvergenzradius ist also 1.orgExponentialfunktion/R/Taylor-Reihe/Aufgabe – Wikiversity

Taylorreihe

Es gilt: für alle Werte von .Eine Exponentialfunktion der Form f(x)=c⋅ax f ( x) = c ⋅ a x soll durch die Punkte (x1 ∣y1) ( x 1 ∣ y 1) und (x2∣y2) ( x 2 ∣ y 2) verlaufen.Sei eine reelle oder komplexe-Matrix.In vielen Anwendungen, beispielsweise in der Physik, ist es ausreichend eine Funktion bis zu einer gewissen Genauigkeit zu kennen.Lexikon der Mathematik Taylor-Reihe.