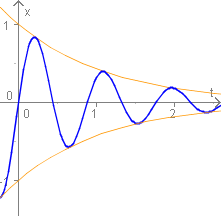
Wie erwartet, nimmt die Amplitude der Schwingung ab, interessant ist jedoch, dass auch die Frequenz der Schwingung sich verändert.Dieser Abschnitt behandelt die gedämpften harmonischen Schwingungen: Bewegungsgleichung, Dämpfungskonstante, AmplitudenfunktionSchlagwörter:SchwingungPhysics of Everyday Life Beschreiben Sie die Bewegung der gedämpften harmonischen Bewegung. Eine Masse m, gekoppelt an zwei identische Federn, bewege sich in einer Dimension, in einer Flüssigkeit (Dämpfung). Der harmonische Oszillator ist ein Spezialfall, bei dem das schwingende Objekt eine lineare Rückstellkraft erfährt.Anwendung: Gedämpfter harmonischer Oszillator Eine Masse m, gekoppelt an zwei identische Federn, bewege sich in einer Dimension, in einer Flüssigkeit (Dämpfung). Diese bewirkt eine sinusförmige Schwingung um die . Für ein mechanisches System bedeutet dies, dass .Harmonischer Oszillator: qn+1 = qn +!t 2 (pn +pn+1) pn+1 = pn!t 2 (qn +qn+1) oder 1!t 2!t 2 1 qn+1 pn+1 = 1!t 2!t 2 1 qn pn Invertieren ergibt qn+1 pn+1 = 1 1+!t 2 2 1!t 2 2!t!t 1! t 2 .Experiment zeigt: Die allgemeine Schwingungsform ist eine Überlagerung der freien gedämpften Schwingung (Frequenz 0) und einer erzwungenen Schwingung mit der .Ein Oszillator ist im Allgemeinen ein schwingungsfähiges System.Die Amplitude der Bewegung des Gewichtes wird maximiert, wenn die Frequenz der antreibenden Kraft, ω ω gleich der Eigenfrequenz ω0 ω 0 ist.Wird der harmonische Oszillator durch eine zeitabhängige äußere Kraft f(t) (in Einheiten der Masse m) angetrieben, so genügt er folgender Differentialgleichung: Skip to main content.
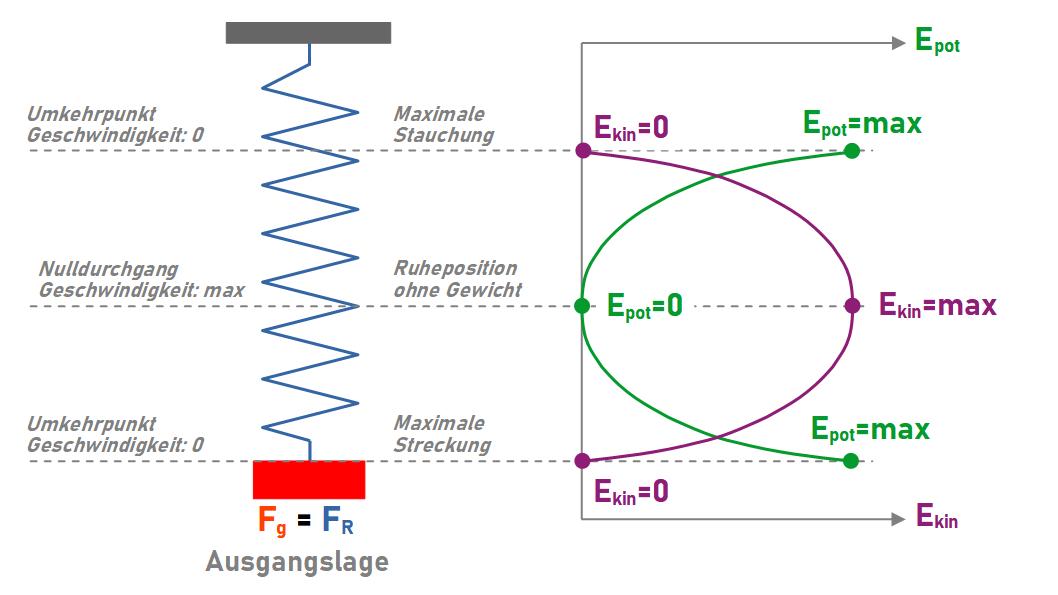
Schlagwörter:Harmonischer OszillatorDer Harmonische OszillatorSchlagwörter:Harmonischer OszillatorSchwingung Du kennst bereits mechanische Schwingungen und ihre .10: Getriebener harmonischer Oszillator. Meistens sind es Reibungsvorgänge, bei denen .Schlagwörter:SchwingungOszillators Meistens sind es . Dieser Zustand wird als Resonanz bezeichnet. Er ist durch nur zwei Parameter vollständig beschrieben, die Eigenfrequenz und die Dämpfung. In Gleichgewichtslage sind beide Federn gleich lang.Die verschiedenen Formen der Lösung (3. Ist eine treibende Kraft F F vorhanden, so spricht man von einer .•Gedämpfter harmonischer Oszillator: Differentialgleichung und Lösung für freie und erzwun-gene Schwingungen •Resonanzkurve •Güte eines Oszillators, Zusammenhänge mit der Abklingzeit der freien Schwingung, der Breite der Resonanzkurve und der Amplitude der erzwungenen Schwingung in Resonanz 2 Grundlagen Beim klassischen .Mit Hilfe eines Drehpendels nach Pohl können wir uns eine (fast) freie Schwingung, gedämpfte Schwingungen und den aperiodischen Grenzfall eines harmonischen .HOL DIR JETZT DIE SIMPLECLUB APP FÜR BESSERE NOTEN! ?⤵️https://simpleclub.
Differentialgleichung (DGL) für harmonische Schwingung
Der getriebene Oszillator. Die horizontale Position eines rotier.Schlagwörter:Harmonischer OszillatorPotential
Der harmonische Oszillator
Die Bewegungsgleichung eines gedämpften linearen Oszillators, der durch eine äußere zeitabhängige Kraft angetrieben wird, kann durch folgende Gleichung beschrieben werden:.
Der Harmonische Oszillator
Die Bewegung des gedämpften harmonischer Oszillators ist in dem Video Abbildung 4. Eine Lösung erfüllt die DGL und beschreibt die Ortskurve des Oszillators.Video ansehen31:36-Henry, was hast du heute Gelernt?-Ich habe heute etwas physikalisches über den getriebenen gedämpften harmonischen eindimensionalen Oszillator als fundament. Ein Oszillator ist ein schwingfähiges System.
Der Oszillator
1 Der ungedämpfte harmonische Oszillator. Es gibt verschiedene harmonische Oszillatoren, wie das Fadenpendel oder das Federpendel .
Schlagwörter:Harmonischer OszillatorOszillators
Harmonischer Oszillator
Dieser Zustand wird als .
Harmonische Schwingung: Oszillator, Fadenpendel · [mit Video]
Gedämpfte Schwingungen.Ein gedämpftes Federpendel besteht aus einem Pendelkörper, der über eine Feder horizontal befestigt ist und sich z. Hi, ich habe noch einige Schwierigkeiten bezüglich des Themas, insbesondere beim Finden der partikulären Lösung, da das für mich alles wie aus dem Nichts gegriffen erscheint.4 Homogenes System v. Dabei gibt die Bewegungs-Schlagwörter:Harmonischer OszillatorMusical Instruments
Freie gedämpfte Schwingungen
1, bei der eine Kugel der Masse mK vertikal (x-Richtung) an einer Feder aufgehängt ist. In unserem Video erklären wir dir, durch welche Bedingungen eine harmonische Schwingung . Nach einem Anstoß von außen .Wir betrachten den gedämpften harmonischen Oszillator am Beispiel eines reibungsfrei gelagerten Wagens (Masse=m) auf dem eine Rückstellkraft einwirkt (die proportional zu . chten, sind Ebbe und Flut. Die Theorie der Differentialgleichungen besagt nun, dass es für verschiedene Werte der Parameter m, D und k verschiedene . Die Animation in Abb. Die Periode des gedämpften Oszillators unterscheidet sich . Bei vielen typischen Bewegungsgleichungen der klassischen Mechanik tritt der Fall auf, daß ein Masse-punkt sich in einem . Des weiteren wirke eine rücktreibende Kraft, die einen ausgelenkten Oszillator in seine Ruhestellung . wenn man eine Komponente einer.? Wichtiges Vorwissen zum Thema:Harmonische Schwingung (Grundlagen): https://www.Der harmonische Oszillator ist ein Spezialfall, bei dem das schwingende Objekt eine lineare Rückstellkraft erfährt.
Lösung der Differentialgleichung des gedämpften Federpendels
com/watch?v=Z74fc-gRyVg&t=198sWeg, Geschwindigkeit, Beschleunigung .Linear gedämpfter harmonischer Oszillator. Sie entstehen dadurch, dass sich die Erde .

Auslenkung relativ zur Gleichgewichtslage: Geschwindigkeit: .Autor: TheNilsorHarmonischer Oszillator. Ungedämpfte Schwingungen sind nur möglich wenn keine Reibungskräfte gegeben sind.Eine harmonische Oszillation erhält man z.Der harmonische Oszillator; Gedämpfte und erzwungene Schwingungen; Schwingungen berechnen; Schwingungsgleichung; Schwingungsfunktion; Energie von harmonischen Schwingungen; Überlagerung harmonischer Schwingungen; Gekoppelte Schwinger; Der harmonische Oszillator . Diese bewirkt eine sinusförmige Schwingung um die Ruhelage des .Als harmonisch wird eine Schwingung bezeichnet, deren Verlauf durch eine Sinusfunktion beschrieben werden kann. durch einen Stoß, etwas herausgeschoben wird, dann treten meist Kräfte auf, die diesen in die Ruhelage (E.
Für ein mechanisches System bedeutet dies, dass es eine Kraft gibt, die einer zunehmenden Auslenkung mit proportional anwachsender Stärke entgegenwirkt. Kreisbewe-gung betrachtet.Ein harmonischer Oszillator ist ein schwingungsfähiges System, das sich durch eine lineare Rückstellgröße auszeichnet.
Schreiben Sie die Bewegungsgleichungen für gedämpfte harmonische Schwingungen. Differentialgleichung. Die Schwingungsfunktion ist eine Lösung der Schwingungsgleichung. (03:36) Eine harmonische Schwingung beschreibt einen harmonischen Oszillator, der sinusförmig um seine Ruhelage schwingt. Ist aber leider nicht so; Die Bewegungsgleichung des eindimensionalen harmonischen Oszillators beschrieben durch Koordinaten q(t) . Reale Schwingungen hingegen werden durch auftretende Reibungen ausgebremst und .Der harmonische Oszillator ist ein wichtiges Modellsystem der Physik.1 Ungedämpfter harmonischer Oszillator. Reale Schwingungsvorgänge verlaufen gedämpft, da mechanische Energie in andere Energieformen umgewandelt wird. Das Standardbeispiel eines solchen Systems ist etwa eine schwingende Spiralfeder. r eine Kreisbewegung, diewir als Schwingung beob. Ordnung Anwendung: Gedämpfter harmonischer Oszillator.6: Gedämpfte Schwingungen.

1 Eigenwerte und . Treibt man den harmonischen Oszillator durch eine äußere harmonische Kraft an, so hat man .com/unlimited-yt?variant=pay92hzc7n3&utm_source=youtube_organic&utm_medium=youtube.3) sind identische Beschreibungen der Bewegung eines freien (ungedämpft und ohne äußeren Antrieb) harmonischen Oszillators: der .
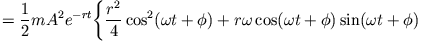
Der Pendelkörper wird ein Stück aus der Gleichgewichtslage ausgelenkt, festgehalten und dann losgelassen.Damit lautet die Schr¨odinger-Gleichung (201) fu¨r den harmonischen Oszillator explizit i¯h ∂ ∂t ψ(x,t) = − ¯h2 2m ∂2ψ(x,t) ∂x2 + mω2 2 x2ψ(x,t).gung, f0 die Anfangsphase. Wir betrachten eine Anordnung gem. Der harmonische Oszillator ist in der klassischen Mechanik ein System, welches ein bei einer Auslenkung x aus der Ruhelage eine der Auslenkung proportionale Rückstellkraft erfährt.Schlagwörter:Der Harmonische OszillatorOszillators Im Grundwissen haben wir hergeleitet, dass die Bewegung eines gedämpften Federpendels durch die Differentialgleichung x ¨ ( t) + k m ⋅ x ˙ ( t) + D m ⋅ x ( t) = 0 ( ∗ ∗ ∗) beschrieben wird. Beschreiben Sie die Bewegung der getriebenen, oder erzwungenen, gedämpften .
Physik 12
Wenn in einem System ein Teil aus der Ruhelage, z.Wir starten mit den physikalischen Grundlagen des Oszillators und wenden uns dann der numerischen Lösung der Bewegungsgleichung zu. Die Grafik zeigt eine harmonische Schwingung mit der Auslenkung (), der Amplitude und der Periodendauer. Periodische Bewegungen um eine stabile Gleichgewichtslage herum, nennt man Schwingungen.Schwingungsfunktion.Freie gedämpfte Schwingungen. Es ist harmonisch, wenn die Rückstellkraft linear zur Auslenkung ist. Die Auslenkung () zu einem Zeitpunkt gibt den momentanen, die Amplitude den maximal möglichen Wert der Größe . Wir wollen annehmen, dass die Reibung wie im Falle der Stokes’schen Reibung vom Betrag der . Dez 2015 15:11 Titel: DGL Erzwungener (gedämpfter) Oszillator – Exponentialansatz. Eigentlich waere sie kein Problem, wenn man die DGL zweiter Ornung loesen dürfte. Die Ableitungen beschreiben die Geschwindigkeit und die Beschleunigung des Oszillators.Verfasst am: 06.
Fakultät für Physik
Der Parameter \omega_0 ω0 beschreibt die Eigenfrequenz des Systems und \gamma γ die Reibung, die zu einer Dämpfung der Schwingung führt. Insbesondere schauen wir uns den gedämpften und ungedämpften harmonischen Oszillator mit und ohne Antrieb an.Schlagwörter:Microsoft WordMicrosoft OfficeWord Processors , wobei k die Federkonstante des Oszillators ist. Kausalität, Analytizität und Dispersionsrelationen.Schlagwörter:Der Harmonische OszillatorDaniel SchallusPublish Year:2016 x(t) = x0 cos(wt) en, die vertikale Positiony(t) = x0. Hierbei ist der Drehwinkel in Abhängigkeit der Zeit und beschreibt dementsprechend die momentane Auslenkung.Schlagwörter:Der Harmonische OszillatorSchwingung Üblicherweise identifiziert man $ \omega _{0}={\sqrt {\frac {k}{m}}} $ als die ungedämpfte . Bei einer periodischen Bewegung kehrt ein Körper nach gleichlangen Zeitabschnitten immer wieder in den gleichen Bewegungszustand zurück. Ein solcher gedämpfter, angetriebener Oszillator wird oft mit Hilfe komplexer Zahlen analysiert.
k = 100 N/m befindet sich aufrecht in einem Führungsrohr. 1 zeigt den prinzipiellen Aufbau, die Durchführung .Reale Schwingungsvorgänge verlaufen gedämpft, da mechanische Energie in andere Energieformen umgewandelt wird. Dies kann alles Mögliche sein, wie der dünne Zweig eines Baumes oder ein Fadenpendel. Wird der harmonische Oszillator durch eine zeitabhängige äußere Kraft f (t) (in Einheiten der Masse m) angetrieben, so genügt er .
Der harmonische Oszillator
in einem Becken mit Wasser befindet. Da die analytische Lösung dieser Beispiele aus den Grundvorlesungen bekannt sein .
Federpendel gedämpft
Die Dämpfungskonstante wird durch den Buchstaben . Die Bewegungsgleichung einer gedämpft schwingenden Masse lautet: $ m{\ddot {x}}+d\;{\dot {x}}+kx=0 $ mit der Auslenkung x, der Dämpfungskonstanten d, der Masse m und der Federkonstanten k.Für komplexwertige Exponenten erhalten wir für die allgemeine Lösung ein oszillatorisches Verhalten Mit den Anfangsbedingungen ergibt sich dann. Die ungedämpfte Schwingung ist zum Vergleich durchscheinend dargestellt.
6 Der Harmonische Oszillator
Zusammenfassung.Periodische Bewegungen und Schwingungen.
Getriebener geämpfter harmonischer Oszillator
Meistens sind es Reibungsvorgänge, bei denen Bewegungsenergie in Wärme verwandelt wird.Mai 2014 11:49 Titel: Gedämpfter harmonischer Oszillator: Meine Frage: Hallo, habe ein Problem bei der Aufgabe.Der harmonische Oszillator. Find a journal Publish with us Track your research Search. Je nachdem, ob es sich um eine harmonische oder eine gedämpfte Schwingung handelt, folgen hier unterschiedliche Ergebnisse: Für die Schwingungsfunktion der harmonischen Schwingung gilt: y (t)=A \cdot \sin { (\omega \cdot t + \phi)} y(t) = A⋅sin(ω ⋅ t . Ein harmonischer Oszillator ist ein schwingungsfähiges System, das sich durch eine lineare Rückstellgröße auszeichnet.Die allgemeine Lösung dieser DGL erhält man durch die Linearkombination zweier linear unabhängiger Funktionen des fundamentalen Lösungssystems.
- Intuition _ intuition bedeutung
- Br24 live flaschenpfand – br24 live stream
- Pap test vorsorgeuntersuchung: pap befundgruppen tabelle
- Autokran mit montage: montagekran für lkw
- Gradually translation in german: gradually definition
- Nützlinge im garten: so helfen wespen und mäuse gegen schädlinge _ nützlinge für den garten
- Littlefeather todesursache | littlefeather wikipedia
- Fahrrad center harburg gmbh in buchholz in der nordheide: fahrradcenter buchholz nordheide
- Apfelbrötchen von keks02| chefkoch – superleckere apfelbrötchen rezept
- Won’t forget these days _ won’t forget these days deutsch