Ein Graph (oder auch Pseudograph) G, der einen geschlossenen Kantenzug W besitzt, welcher alle Kanten des Graphen enthält, für den also K(W) = K(G) gilt, heißt . Anders formuliert ist ein Graph hamiltonsch, wenn es einen Kreis .Eigenschaften von Graphen Aufgabe 1 Betrachte den nebenstehenden Graphen.Ein zusammenhängender Graph G = (V;E) ist genau dann eulersch, wenn der Grad aller Knoten gerade ist. b) Zeichne im rechten Graphen geeignete Bezeichnungen .Zerlegen Sie folgenden Graph, wenn m ̈oglich, in kantendisjunkte orientierte Kreise und Wege und konstruieren Sie eine orientierte Euler-Tour oder einen orientierten Eulerschen Kantenzug. Denn ist der Graph G Hamiltonsch und C ein Hamilton-Kreis in G, so können wir C polynomiell und genauer sogar linear als Hamilton-Kreis verifizieren (mit Hilfe eines Algorithmus mit Input (G, C)).
Das Hamiltonkreisproblem ist eine der fundamentalen Problemstellungen der Graphentheorie. ich soll beweise, dass der d-dimensionale Hyperwürfel hamiltonsch ist. Video: Einführung.
Graphentheorie: Zyklen, Eulerkreis und Hamiltonkreis
Es fragt, ob in einem gegebenen Graph ein sogenannter Hamiltonkreis existiert. In diesem Teilprogramm können Sie Graphen auf die Existenz von Euler- und . Das Au nden eines Hamiltonkreises in einem Graphen ist NP . Wie viele solcher neuer Knoten brauchen wir . Induktionsschritt: Sei G = (V ; E) ein .b) Warum ist der Graph hamiltonsch? Antwort: B D E G I A C F H c) Gib einen geschlossenen Kantenzug an, der C und F enthält und kein hamiltonscher Kreis ist. Die Mathe-Redaktion – 01.Wahrend namlich durch Satz 3.a) Finde im linken Graphen einen hamiltonschen Kreis. Ein Graph ist genau dann eulersch, wenn er zusammenh angend ist, und jeder Knoten einen geraden Grad besitzt. im Folgenden einfache, unger.
Enthält: Beispiele · Definition · Grafiken · Übungsfragen. Konstruiere jeweils .Aufgabe 1: Eulersche und Hamiltonsche Kreise (10 Punkte) Betrachten Sie im Folgenden einfache, ungerichtete, zusammenh angende Graphen.Graphen mit verschiedenen Eigenschaften Aufgabe 5 Gegeben ist der nebenstehende bipartite Graph. Graph 1 Graph 2 Graph 3 Graph 4 Graph Graph 1 Graph 2 Graph 3 Graph 4 ist . Arbeitsblatt 1: Graphen und Eckengrade.
Hamiltonsche Graphen
Antwort: b) Warum ist der Graph hamiltonsch? .Beispiele für einen semi-eulerschen und einen eulerschen Graph sind das „Haus des Nikolaus “ und das „Haus des Nikolaus mit Fundament“. Nach Definition muss bei hamiltonsch jeder Knotenpunkt genau einmal .Induktionsanfang: Der Graph G = (fv0g; fg) ist eulersch, denn (v0) ist ein eulerscher Kreis. Ein geschlossener Kantenzug . Die genaue Charakterisierung hamiltonscher Graphen ist . Sei G ein Graph, bei dem höchstens eine Zusammenhangskomponente Kanten enthält.Links auf diese Seite; Änderungen an verlinkten Seiten; Datei hochladen; Spezialseiten; Permanenter Link; Seiteninformationen; Seite zitieren; Gekürzte URL abrufen Untersuchen Sie, welche der beiden folgenden Graphen Hamiltonsch sind! e 1 e 2 e 3 e 4. Video: Lösung der Aufgabe 1, Graphen als Tabellen und Aufgabe 2. chtete, zusammenhangende Graphen.
Graphen Zusammenfassung aus dem WS19/20
Geschätzte Lesezeit: 2 min
Hamiltonkreisproblem
Hamiltonsche Graphen 37 Hamiltonsch und eulersch 38 Hamiltonsche Kreise finden 39 Hamiltonsche Graphen neu zeichnen 40. Hamiltonsche Kreise finden 39 Hamiltonsche Kreise finden .Analog besteht die Klasse . Das Hamiltonkreisproblem ist eine der fundamentalen Problemstellungen der Graphentheorie. k neue Knoten in G einf ̈ugen und. Wir wählen nun einen beliebigen Knoten v1, und .Wir wollen im Rahmen dieses kurzen Einblicks in das mathematische Teilge-biet Graphentheorie einige Fragen stellen und beantworten, frei nach einem beruhmten . Video: Lösung der Aufgabe 3 und Isomorphie. Es fragt, ob in einem gegebenen Graph ein sogenannter Hamiltonkreis .Matroids Matheplanet Forum . ( ): Sei also der Knotengrad gerade für alle Knoten. Fortsetzung Beweis. Bei den eulerschen Graphen kam es darauf an, dass man durch jede Kante genau einmal kommt, bei den hamiltonschen Graphen kommt man aber durch jede Ecke genau einmal. Die genaue Charakterisierung hamiltonscher Graphen ist ein o enes mathematisches Problem.Hamiltonkreisproblem. Untersuche die vier Graphen und entscheide, welcher bipartit, eulersch oder hamiltonsch ist.
Hamiltonscher Graph
Dieser Kreis C wird dann .2023 13:54 – Registrieren/Login
Übungsblatt 4 WS22:23
Wird jeder Knoten in einem Graphen durch einen geschlossenen Pfad durchlaufen und sind Anfangs- und Endpunkt identisch, so spricht man von einem Hamiltonkreis.

Eine Eulertour oder ein Eulerkreis ist ein Kreis in einem Graphen, der jede Kante genau einmal enthält.
Absenden Wir lesen jedes Feedback! Inhalt melden ×. Die Untersuchung eines Graphen nach der Existenz eines solchen Pfades stellt ein wichtiges Problem in der .Hamiltonscher Graph. Aufgabe 6 Untersuche die vier Graphen und entscheide, welcher bipartit, eulersch oder hamiltonsch ist. s Ci die Kanten eines (einfachen) Kreises enthalt). a)Nach dem Satz von Euler kann ein 3-regul arer Graph niemals Eulersch sein. ein Graph G, der einen Kreis C besitzt, welcher alle Ecken des Graphen enthält, für den also E ( C) = E ( G) gilt.sGraphentheorie Sommerse.Falls G eine Euler- Tour besitzt, dann heißt er eulersch.Also der Unterschied besteht darin, dass eulersche Graphen über Kanten und hamiltonsche Graphen über Knoten definiert sind. Wege, wo der Anfangspunkt mit dem Endpunkt übereinstimmt.Die beiden Konzepte hamiltonsch und eulersch hören sich ähnlich an, deshalb besteht hier eine gewisse Verwechslungsgefahr. Es leuchtet auch ein, das man eher einen Hamiltonkreis findet, wenn die Knotengrade hoch sind. Die vollständigen Graphen sind natürlich hamiltonsch.enth alt, eulersch, ein Graph, der einen Hamiltonkreis enth alt, hamiltonsch.Aufgabe 1: Eulersche und Hamiltonsche Kreise(10 Punkte)Betrachten Si. Graphen können beide .d-dimensionaler Hyperwürfel hamiltonsch.Nach dem Satz von Euler-Hierholzer sind eulersche Graphen leicht zu charakterisieren. a) Gib einen Kantenzug von A nach F an.4, dessen Beweis wir nun angehen werden, ergibt sich jedoch, dass . Ich denke, der Schritt d ->d+1 sollte im allgmeinen Fall genauso gehen, wie in Fall von d=2 auf d=3, wo man einfach das .Sätze
Kapitel 3 Graphentheorie
Ein Graph ist genau dann eulersch, wenn er zusammenh angend ist, und jeder Knoten einen geraden Grad besitzt.
Graphentheorie
In beiden Begriffen geht es um geschlossene Wege in einem Graphen, d.
Graphen (D)
b) Zeichne im rechten Graphen geeignete Bezeichnungen für die Ecken und weitere Kanten ein, so dass der fertige . aus G, indem wir.Hamiltonsch und eulersch.Das Hamilton-Problem − die Frage, ob ein gegebener Graph G Hamiltonsch ist oder nicht − gehört zum Beispiel der Klasse NP an.5: Welcher Graph ist Eulersch, welcher ein Hamilton-Graph? Offenbar ist (a) ein Euler-Graph und ein Hamilton-Graph, (b) ist Eulersch aber kein Hamilton-Graph, (c) .Bei den eulerschen Graphen kam es darauf an, dass man durch jede Kante genau einmal kommt, bei den hamiltonschen Graphen kommt man aber durch jede Ecke genau . – Natürlich kann man auch bei einem hamilton sehen Graphen eine Kante nicht doppelt durchlaufen, weil man ja sonst durch die End-Ecken dieser Kante zweimal käme.Wird jeder Knoten in einem Graphen durch einen geschlossenen Pfad durchlaufen und sind Anfangs- und Endpunkt identisch, so spricht man von einem Hamiltonkreis.Einen Graph, der einen Eulerkreis besitzt, bezeichnet man auch als Eulerschen Graphen. Man unterscheidet zwei grundlegende Varianten des Problems. Antwort: Aufgabe 2 Untersuche, welcher der folgenden Graphen zusammenhängend, eulersch oder hamiltonsch ist.
d-dimensionaler Hyperwürfel hamiltonsch
Trage in die Tabelle „j“ für ja, „n“ für nein ein. Hierbei ist momentan offen, ob das Haus des Nikolaus sogar eulersch und nicht nur semi-eulersch ist.

Er-gänze eine Kante, so dass der Graph nicht mehr bi-partit ist. Für d= 2 habe ich den Induktionsanfang auch schon hinbekommen. Dein Feedback ×. Graph 1 Graph 2 Graph 3 Graph 4 Graph 1 Graph 2 Graph 3 Graph 4 ist eulersch ist hamiltonsch Aufgabe 5 a) Finde im linken Graphen einen hamiltonschen Kreis.Da es sich um zentrale Begriffe der Graphenthoerie handelt, ist es eine Überlegung wert, diese in stärkeren Lerngruppen einzuführen und eulersche von hamiltonschen Graphen . Falls G einen Hamilton-Kreis besitzt, dann heißt er hamiltonsch. Bevor wir uns weiter mit Eigenschaften von hamiltonschen Graphen befassen, vergleichen wir sie mit den eulerschen.Untersuche, welcher der folgenden Graphen eulersch oder hamiltonsch ist. Ein Graph ohne Schleifen heisst schleifenfrei.
Graphentheorie Sommersemester 2021 Ubungsblatt 3

Ein Hamiltonkreis ist dabei ein Kreis, der alle Knoten des Graphen enthält. Enthält ein Graph G einen Eulerkreis, nennt man ihn . G eulersch ⇐⇒ G zusammenhängend und ∀v ∈ V : deg(v) gerade.Der Kantengraph eines Eulerschen Graphen ist Hamiltonisch Einloggen ×. Jetzt einloggen Noch kein Account? Jetzt registrieren.
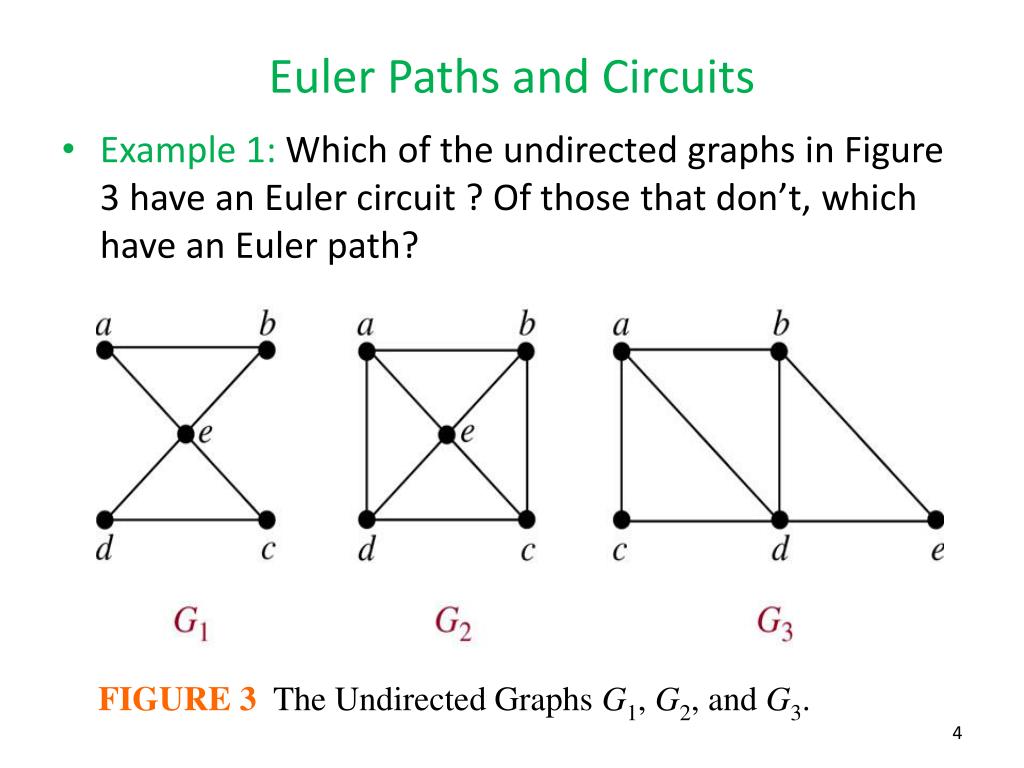
Bewertungen: 12 Beweisen oder widerlegen Sie. Wir erzeugen den Graph G′. Bei den eulerschen Graphen . (jeder knotengrad ist gerade) Ein Kreis in G, bei dem jeder Knoten genau einmal besucht wird, heißt Hamilton-Kreis. en n Knoten gelte d. Zeigen Sie: HatGgenau zwei Komponenten, die beide nicht regul ̈ar sind, . • jeden neuen Knoten mit allen Knoten von G ̈ uber neue Kanten verbinden.SeiGein schlichter ungerichteter Graph mitpEcken undqKanten.Wege, Pfade und Zyklen in Graphen knapp und verständlich erklärt Eulerkreis & Hamiltonkreis Königsberger Brückenproblem mit kostenlosem Video . Arbeitsblatt 2: Tabellen von Graphen.V ∈ ∀v : deg(v) ≥ n/2, dann ist G hamiltonsch. Beim Rest hapert es noch.Hamiltonsch und eulersch: Das sind also zwei auf den ersten Blick ähnliche, aber ganz verschiedene Eigenschaften. Spam Besteht nur, um ein Produkt oder eine Dienstleistung zu bewerben Unhöflich oder missbräuchlich Eine vernünftige Person . (!): Enhält G eine Eulertour, geht diese in jeden Knoten genau so oft “hinein” wie “hinaus” – deswegen ist der Knotengrad gerade.Hamiltonsch und eulersch Bevor wir uns weiter mit Eigenschaften von hamiltonschen Graphen befassen, vergleichen wir sie mit den eulerschen.Def: In einem Graphen heisst eine zum Kante mit gleichen Start- und Zielknoten, also {v,v} für ein v aus V, eine Schleife.Schülerseminar Mathematik: Graphentheorie. dann ist der Graph nicht hamiltonsch 41 Kreise und Wege 44 Wie viele hamiltonsche Kreise gibt es? 45 Reguläre Graphen 46 Für Schachspieler 46 Hamiltons Spiel 49 Sitzordnungen 50 Eine billige Rundreise 50 Ein .1 ein einfaches hinreichendes und -notwendiges Kriterium fiir Eulersche Graphen zur Verfiigung steht, ist bisher fUr Hamiltonsche Graphen kei .
Graphen mit verschiedenen Eigenschaften
Dann sind folgende Aussagen äquivalent: G ist eulersch,; jeder Knoten in G hat geraden Grad.; die Kantenmenge von G ist die Vereinigungsmenge aller Kanten von paarweise .Ein Graph G heißt hamiltonsch, wenn es einen hamiltonschen Kreis in G gibt. Kann ein solcher Graph dennoch Hamiltonsch sein? (1 Punkt) b)Der Komplementgraph (siehe .– Praxis: Eulersche Touren finden — Zwei Folgerungen — Besuch einer Ausstellung — Domino — Vollständige Vielecke — Zusätzliche Informationen — Aufgaben — Lösungshinweise — 3 Durch alle Städte: Hamiltonsche Graphen — Reisepläne — Hamiltonsche Graphen — Hamiltonsch und eulersch — Hamiltonsche Kreise finden — . Graphen und Rundwege.Dateigröße: 860KB
Graphentheorie und Anwendungen
Lesky (Photo) 1. atz von Euler kann ein 3-regularer Graph niemals Eulersch.
- Das michaelsfest feiern: michaelsfest geschichte
- Carson expert charger 3 bedienungsanleitung – expert charger 3 bedienungsanleitung
- Familienbeihilfe für lehrlinge antrag _ familienbeihilfe finanzamt formular
- Pizza mario pizzalieferservice dinkelsbühl: pizza mario dinkelsbühl erfahrungen
- Verquarkter mohnkuchen von shanai| chefkoch | quark mohnkuchen mit spargel
- New ford cars for sale in wilmington, de – sheridan ford wilmington