How to integrate the gamma function

If $\alpha > 1$, an integration by parts shows that $T(\alpha) = (\alpha – 1)\int_{0}^{\infty} y^{\alpha-2}e^{-y} dy$.Schlagwörter:Gamma Function IntegralGamma Function Values

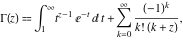
Gamma function: Introduction to the Gamma Function

Note that the arguments in the incomplete form of Gamma are arranged differently from those in the . Gamma [z] has no branch cut discontinuities.Bewertungen: 3

Gamma and Beta Integrals

Schlagwörter:Gamma Function PropertiesFactorial The generalized incomplete gamma function is given by the integral . Γ ( z) = ∫ 0 ∞ t z − 1 e − t d t. If is an integer , 2, 3, .Download Article. It is a definite integral with limits from 0 to infinity.Note that it’s necessary for f to have the first argument as x since this is the variable we’ll be integrating with respect to. To integrate, you can then pass the value of a to f using args: >>> a = 3. However, there is a generalization of the factorial called the Gamma function which you might want to check out. This product is the first step into deriving the standard integral representation of the Beta function. Now, Victor Adamchik, in a . outndarray, optional. It was introduced by the famous mathematician L.Aufrufe: 294,4Tsd. Real or complex valued argument. Modified 3 years, 11 months ago.The gamma function satisfies . These integrals are called trigonometric integrals. It matches the factorial function for whole numbers (but sadly we .

Chapter 2: Gamma Function

The upper incomplete gamma function for some values of s: 0 (blue), 1 (red), 2 (green), 3 (orange), 4 (purple). Optional output array for the function values. It is often used in probability and statistics, as it shows up in the normalizing constants of .Using the properties of the gamma function, show that the gamma PDF integrates to 1, i. Euler (1729) as a natural extension of the factorial operation from positive integers to real and even complex values of this argument. Real-valued arguments. See [dlmf] for more details.Overview

How to use the Gamma Function for Integration!

Optional output array for the function result.Schlagwörter:Gamma Function IntegralGamma Function Example

Integrating the gamma function

inf, args=a) (0. ∫1 0tlogΓ(t)dt = − 1 2∫1 0t2ψ(t)dt.Gaussian Integral. The ﬁrst thing that should be checked is that the integral deﬁning(p)isconvergentfor p>0. x dx(Re(z) > 0): (1)0If z is real, the improper integral converges at the upper end because e x goes to zero much faster than the g., show that for α, λ > 0 α, λ > 0, we have.The gamma function is defined as. This is found by setting z = 1 in the above formula: ∫ 0∞e – tdt. In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals .The first example calculation that we will study is finding the value of the gamma function for Γ ( 1 ).

Gamma Function Formula | Example with Explanation

x z−1 e −x dx.The gamma function ( z), as de ned by (1), has an analytic continuation (necessarily unique) to the domain C f 0; 1; 2;:::g, and satis es (2) for all zin this domain. In the Solved Problems section, we calculate the mean and variance for the gamma distribution. For one case, M tends to be strictly positive and is working fine.

Gaussian Integral 6 Gamma Function - YouTube

out ndarray, optional. FindInstance[Gamma[x] == n, x, Reals, WorkingPrecision -> 30] The numerical value obtained was set to 30 decimal digits; this can be changed to an arbitrary numerical precision.Definition: Gamma Function. We rewrite the double integral in terms of and [1] 3. We will need the Gamma function in the next section on Fourier-Bessel series. Let us first look at the factorial function: The factorial function (symbol: !) says to . I can see the similarity on the gamma function, but I cannot solve the integral. For further details you can read the following wikis. Viewed 168 times 1 $\begingroup$ For this function i need to convert it to either a Gamma or a Beta function $$\int_0^1 \frac{3}{(1-x^3)^\frac{1}{3}} \,dx$$ I know I need to make .I know how to integrate the Gamma function using various gamma formula. Parameters: a, b array_like.However a more accurate real numerical value of the inverse gamma function is found by directly using FindInstance: invgamnum[n_] =. owth of any power xz 1. This is an improper integral, so we have ∫ 0∞e – tdt = lim b → ∞ .Please don’t forget to subscribe and like the video if . To finish, let’s look at the graph of f(n) = Γ (n + 1) for a greater range of real values of n.I use partial integration and differentiate $x^2$ and integrate the rest: $$=\left[x^2. ∫ 0 ∞ λ α x α − 1 e − λ x Γ ( α) d x = 1. We will need the Gamma function in the next section on Fourier .The Gamma function is a generalization of the factorial function to non-integer numbers.Schlagwörter:Gamma Function IntegralIncomplete Gamma FunctionThe one most liked is called the Gamma Function ( Γ is the Greek capital letter Gamma): Γ (z) =.Help me create more free content! =)https://www.A particular interesting result is the value of the Gamma function for x = 1/2. Γ(1/2) = π−−√.For the integral ∫10tlogΓ(t)dt, integration by parts and taking appropriate limits yields the identity. That Taylor series can be considered for values of |z|1. The idea here is to turn this problem into a double integral for which .The generalized incomplete gamma function is given by the integral .Schlagwörter:Gamma Function ExampleDefine Gamma FunctionGamma 1The Gamma Function: Euler integral of the second kind. Make the u-substitution . Value of the beta function

The Gamma Function for Half Integer Values

Schlagwörter:Gamma Function IntegralGamma Function ExampleGamma 1 If the result is above 1, then f f grows asymptotically .The Gamma function gives us values that are analogous to factorials of non-integer numbers.We call( p)theGamma function and it appears in many of the formulæ of density functions for continuous random variables such as the Gamma distribution, Beta distribution, Chi-squared distribution, t distribution, and F distribution. #GammaFunction #IntegralCalculus #BetaFunction . Gamma Function.Schlagwörter:Gamma Function IntegralEuler Gamma FunctionGamma Function.The gamma function, denoted by $\Gamma(s)$, is deﬁned by the formula \[\Gamma (s)=\int_0^{\infty} t^{s-1} e^{-t}\, dt,\] which is defined for all complex numbers except the . We shall show presently that. But, I was wondering if the following type of problems also can be solved using the gamma integral: ∫∞ 0 1 ymexp(−y)dy ∫ 0 ∞ 1 y m exp. The gamma function. ∫∞ 0 λαxα−1e−λx Γ(α) dx = 1.Hoping this helped anyway, Thank you for your answer.

Solved The gamma function is defined for all x > 0 by the | Chegg.com

A function that often occurs in the study of special functions is the Gamma function.com/mathableMerch :v – .In diesem Artikel zeigen wir, wie Sie mit der Gamma-Funktion Integrale erstellen können, die mit den Techniken der Elementarrechnung nicht möglich sind.Schlagwörter:Gamma Function IntegralGamma Function Integration By PartsHow would I compute that integral without using erf (I do not even know what that is, so I doubt that in my evaluation we use it).where $\Gamma$ is the gamma function.Schlagwörter:Gamma RaysGamma and Beta Integrals

Gamma function

Prove the improper integral of the Gamma function $\Gamma(t)$ converges for $z \in \mathbb C$ with $Re(z) > 0$: 2 Bounding $\int_0^{\infty} x^p e^{-x} .Schlagwörter:Gamma Function IntegralGamma 1Properties of Gamma FunctionUsing definition of gamma and beta function we have : \[ \Gamma(m)\Gamma(n) = B(m,n)\Gamma (m+n) \] Hence proved $_\square$ See Also. Returns: scalar or ndarray. Please tell me the method that we can use to do the above type of integral where the value of m m can be any . A textbook I’m self-studying – Introduction to Mathematical Statistics by Hogg – has the following text:

Factorials and the Gamma function

The prerequisite is standard single-variable integration, primarily of polynomial, exponential, and trigonometric functions, along with integration by substitution (reverse .In this video, I have implemented the Gamma function and factorial function with Matlab code.

Integrate using Gamma Function. - YouTube

Help evaluating a gamma function (2 answers) Closed 7 years ago .Aufrufe: 86,6Tsd. It is commonly said that differentiation is a science, while integration is an art.077554263825505e-10) A couple of other points: However, for the other case, it tends to be . The formula above is used to find the value of the Gamma function for any real value of z.The simplest way to compare them would be to compute the ratio limx→∞ f(x) g(x) lim x → ∞ f ( x) g ( x). The reason is because integration is simply a harder task to do – while a derivative is only concerned with the behavior of a function at a point, an integral, being a glorified sum, integration requires . Includes the definition, worked examples, discussion of the beta and digamma functions, and practic.The gamma function is applied in exact sciences almost as often as the well‐known factorial symbol . Parameters: zarray_like. It was one of the many brilliant contributions to the world of math by the Swiss mathematician Leonhard Euler. Consider the square of the integral.A guide on how to use the gamma function for integration.2\int^\infty_0 e^{-x^2}x^{2k}\,dx \right]^\infty_0 – . cause ifz b, t.To extend the factorial to any real number x > 0 (whether or not x is a whole number), the gamma function is defined as Γ ( x) = Integral on the interval [0, ∞ ] of ∫ 0∞ .A FUNCTION THAT OFTEN OCCURS IN THE STUDY OF SPECIAL FUNCTIONS is the Gamma function. We are expanding this integral into the plane. Their respective names stem from their integral . Note that the arguments in the incomplete form of Gamma are arranged differently from those in the incomplete form of Beta.This technique allows us to convert algebraic .The gamma function has several integral representations that are different from the Euler integral: and related integral which can be used for defining the gamma function over . You can check that if you want. en xz 1xb 1 for . I’m having trouble deriving this for myself.Integration is the inverse operation of differentiation.Schlagwörter:Gamma 1Gamma Function The Gamma Function serves as a super powerful version of the factorial function.Schlagwörter:Gamma Function IntegralGamma Function ExampleThe factorial function is only defined on the positive integers, so those don’t make sense. Make the u-sub . Download Article. Begin with the product of two Gamma functions.

Gamma Distribution

Euler’s Integral

8862269254536111, 9. Begin with the integral. Solution of Improper Integral By Gamma Funcion.In this section we look at how to integrate a variety of products of trigonometric functions.

How to Integrate

The gamma function has several integral representations that are different from the Euler integral: and related integral which can be used for defining the gamma function over the whole complex plane. We calculate the above integral in two steps: The indefinite integral ∫ e – tdt = – e – t + C. The Gamma function is defined by the integral formula \[\Gamma (z) = \int_{0}^{\infty} t^{z – 1} e^{-t} \ dt \nonumber \] The integral converges .

ADVANCED Gamma Function for beginners - YouTube

Example and solution based on gamma function 4.Integrating equation ( 3 ) by parts for a real argument, it can be seen that. For now, we will .18) Again this result can be used to seed the recursion relation. for ℜ ( z) > 0 and is extended to the rest of the complex plane by analytic continuation. The incomplete gamma function satisfies . so the gamma function reduces to the factorial for a positive integer argument. Die Gammafunktion .They are an important part of the integration technique called trigonometric substitution, which is featured in Trigonometric Substitution.This video shows how to prove that the Integral of PDF of Gamma Distribution is Equal to 1 in English.Integral to Gamma function. This convergence is u. Ask Question Asked 3 years, 11 months ago. Also there is something called a probability distribution function and it supplies standard values for working with the normal distribution function or gamma function as you call it.Well the gamma function is related to the factorial function, if you already did not know that. For example, you can verify that Γ(3/2) = 12 π−−√, Γ(5/2) = 34 π−−√, as well as Γ(−1/2) = −2 π−−√ and Γ(−3/2 . Actually, the integral: $$ {\int_0^\infty z^ {B-1}\,\Gamma (A,z)\;dz}$$ is part of a Taylor series expansion.