THE MAXWELL-BOLTZMANN DISTRIBUTION FUNCTION
Distribution of Molecular Speeds
Maxwell pictured the gas . The function that describes this distribution is . This speed-distribution function can be derived from the Maxwell-Boltzmann statistics and used to derive relationships between pressure, volume and temperature. The distribution, which describes the kinetic energy of air particles in a particular sample, was devised by James C.
Integrating Maxwell-Boltzmann Distribution
According to the (classical) Boltzmann probability distribution, the probability density .1 : Maxwell (left) and Boltzmann (right) are responsible for describing the velocity distribution of gas molecules. Hi Harikrishnan, the answer by Kåre should be suffcient, however let me stress a very important fact, that the exponential function depends on all momenta p = (p1,p2, p3) (their number equals the dimention of the confiquration space of the particle), and only after suitably performed change of the independent variables one gets the . The length of each side of the box is equal.σ = (3/2)1/2kT=1. Besides the presumption of distinguishability, classical statistical physics postulates further that: There is no restriction on the number of particles which can occupy a given state. Juli 2019quantum mechanics – In what limit do we *really* get Maxwell-Boltzmann .The Boltzmann Distribution. If we were to plot the number of molecules whose velocities fall within a series of narrow ranges, we would obtain a slightly asymmetric curve known as a velocity distribution. Using Boltzmann . time will be measured in nanoseconds. As T → 0, the parameter β = 1/kT → ∞, and the number of populated states → 1, the lowest (ground) state, i.Maxwell-Boltzmann statistics describe the distribution of ideal gas molecules over various energy states. ϵmin − μ T ≫ 1.The normalized Maxwell-Boltzmann velocity distribution function (or probabil-ity density function) of a perfect gas in one dimension is given by [12] ( ) 12 2 exp 2π 2 x x m mv fv kT kT = − . Consider the fraction of molecules in a three-dimensional box having the translation energy ε, then, as a function, it will be: ε = h2 / 8m [nx2 + ny2+ nz2]/ [Lx2 + Ly2 + Lz2] n. To represent the probability for a given energy, it must be normalized to a probability of 1 : This normalized distribution function can then be used to evaluate the mean or average energy. Since this probability function depends upon the specified velocity u, F = F (u) and is defined such that F (u .
Let the total number of particles in the system be ‘n’. n2 n1 = e − ΔE / kBT. tscale = 1e9 # i.Your equation (2) is plain wrong (in one space dimension)! You must express dv in terms of dw, plus a prefactor, to .Maxwell Boltzmann Derivation.Maxwell’s finding was later generalized in 1871 by a German physicist, Ludwig Boltzmann, to express the distribution of energies among the molecules.
PHY141 Lectures 22,23 notes
Explore the relationship between Tempera. • The distribution of energy for a single ideal gas molecule is broad.The Boltzmann distribution represents a thermally equilibrated most probable distribution over all energy levels.Joachim Domsta. If equation (\ref {z}) is to be a relativ frequency (= .Geschätzte Lesezeit: 14 min 2 = nx2 + ny2+ nz2 ,and. In an ideal gas, the total energy is the sum of one-molecule energies and the probabilities for energies in different molecules are uncorrelated. The distribution of speed v is given by the following formula:
Standard Maxwell-Boltzmann distribution: Definition and Properties
sbar = 353 * rscale / tscale # Time step in scaled .The particles are initialised with uniformly-random positions and a fixed speed (randomly-oriented in direction).2em}{0ex}}\text{K}[/latex] that have speeds between 600 m/s and 800 m/s. The Boltzmann factor is used to approximate the fraction of particles in a large system. After an initial relaxation period, their speed .In statistics the Maxwell–Boltzmann distribution is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.Thus, here is how I like to obtain the Maxwell-Boltzmann distribution.In the mid to late 1800s, James Clerk Maxwell and Ludwig Boltzmann figured out the answer to this question.Consider a canonical ensemble of a single particle in a 1D container of length L. For this, the . The total volume of the system is fixed and is given by ‘V’.This normalization will be discussed in more detail in the following. Weitere Ergebnisse anzeigen We now want to know the number of .The normalization can be found using the partition function or by direct integration over volume in velocity space.Despite its importance, in the introductory disciplines of exact science courses, the demonstration of the Maxwell-Boltzmann velocity distribution law is not explained, only its final equation is shown. Their result is referred to as the Maxwell-Boltzmann . To understand this figure, we must define a distribution function of molecular speeds, since with a finite number of . The Boltzmann factor is given by: exp(−βEi) (2.Maxwell – Boltzmann distribution for molecular velocities The velocity distribution is derived for an ideal gas based on very simple assumptions: • The distribution of velocity .The proportionality constant k k (or kB k B) is named after him: the Boltzmann constant.

Geschätzte Lesezeit: 6 min
Maxwell
r = 2e-10 * rscale # Scale time by this factor, in s-1. Once we know the probability distribution for energy, we can calculate thermodynamic properties like the energy, entropy, free energies and . The value of a square is its length as measured on the x-axis times its height as measured on the y-axis, with the units given on those .Lesson: Derive the function of the relative number of molecules travelling at a given speedGoal: I should be able to. For a single free particle the distribution of energy is proportional to the kinetic energy.$\begingroup$ This is more for confirming myself, but, rephrasing @Sebastian Riese, it seems to me, that the Wiki article states that particle momenta are normally (Gaussian) distributed, while energies (speeds) follow chi-squared distribution.The Maxwell-Boltzmann distribution is the distribution of the speeds of ideal gas particles.The Maxwell-Boltzmann distribution is the classical distribution function for distribution of an amount of energy between identical but distinguishable particles. εi = n2h2/8mL2.Weitere InformationenThis predictable distribution of molecular speeds is known as the Maxwell-Boltzmann distribution, .Mathematically, the Maxwell–Boltzmann distribution is the chi distribution with three degrees of freedom (the components of the velocity vector in Euclidean space ), with a . Consider a system that consists of identical yet distinguishable particles.


000 realizations of the standard Maxwell-Boltzmann random variable í µí°µ using Eq.Maxwell-Boltzmann Distribution Function. In simple terms, the kinetic energy of a particle in a system is a particle’s speed.Complete the justification of Boltzmann’s distribution law by computing the proportionality constant \(a\).Key Result: The Boltzmann distribution gives the distribution of particles that corresponds to the most probable populations and is given by the formula: ni N = e − Ei / kBT ∑ie − Ei / kBT.
Maxwell
This predictable distribution of molecular speeds is known as the Maxwell-Boltzmann distribution, after its originators, who calculated it based on kinetic theory, and it has since been confirmed experimentally (Figure \(\PageIndex{1}\)). Hence, Maxwell-Boltzmann can be seen as either, depending on what one takes as an . By varying the molecular weight and temperature you can see how these parameters affect . Maxwell and Ludwig Boltzmann. Each component of the velocity vector, $\{v_x, v_y, v_z\}$ , is normally distributed: This follows from the fact that we obtain a normal distribution (= Gaussian), if we have many independent random processes which contribute equally to the observable variable. The ratio of the number of particles between any two energy levels is.THE MAXWELL-BOLTZMANN DISTRIBUTION FUNCTION In this exercise you will use Excel to create a spreadsheet for the Maxwell-Boltzmann speed distribution and then plot the speed distribution for particles of two different molecular weights and temperatures. The distribution of molecular velocities in a gas, established first by Maxwell and later proved rigorously by Boltzmann, is given by a function F and is today known as the Maxwell-Boltzmann velocity distribution function.
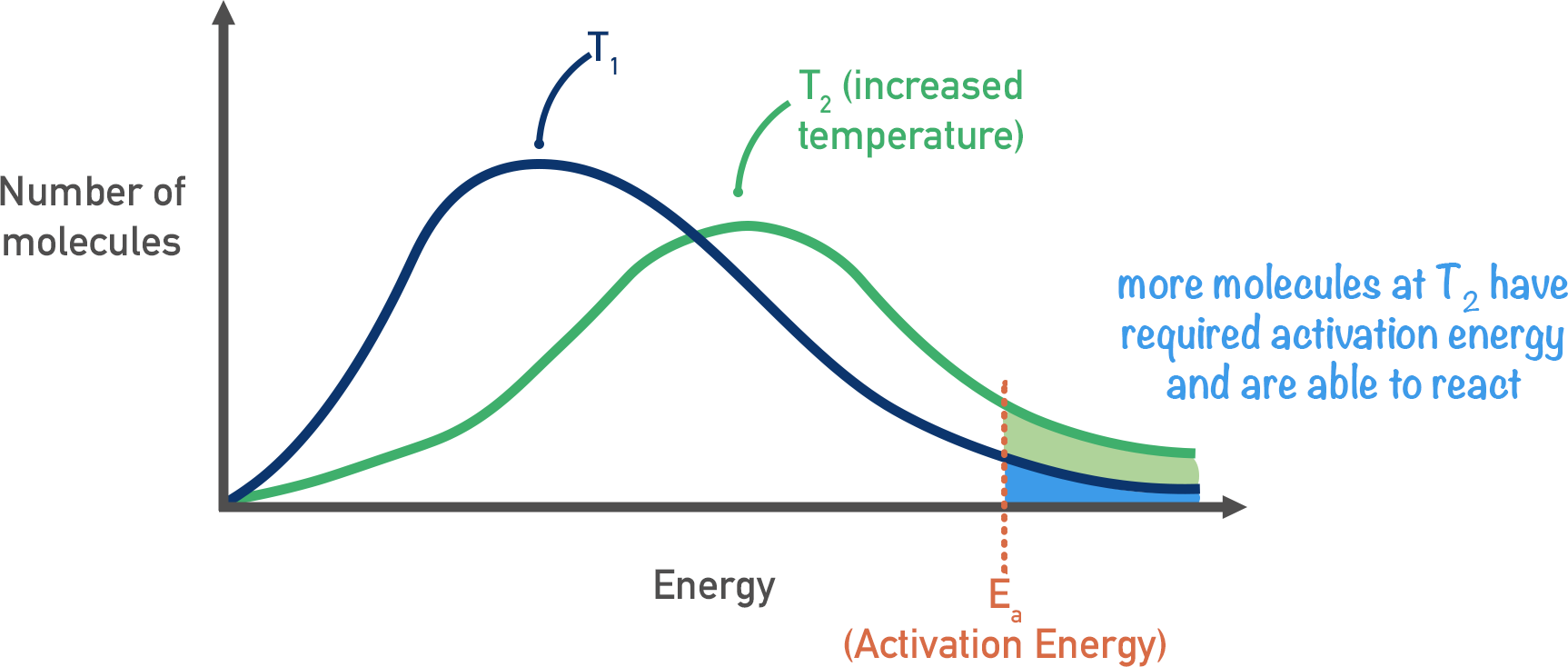
2 we saw that the distribution function for molecular speeds in the x direction .The Maxwell-Boltzmann distribution is derived from the kinetic theory of gases, which states that gas particles move randomly and independently of each other.The peak of this curve would correspond to the most probable velocity. The curve is correctly normalized.It can be used to evaluate the average energy per particle in the circumstance where there is no energy-dependent density of states to skew the distribution. Convolution: Maxwell – Boltzmann distribution for the energy of 2 molecules.Conclusions regarding the partition function: Indicates the number of thermally accessible states in a system.Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu. It was first defined and used .
Maxwell
What is the Maxwell-Boltzmann distribution?
e6 # Use the van der Waals radius of Ar, about 0.

Thus: mv2 m ( vx 2 +vy 2 +vz 2 ) ) ( v F e . It plays a central role in all statistical thermodynamics.Thus the density function is thus ˆ N(t) = N 1 Nu 1 t Nu N 2; t2[0;Nu] Send n!1, we obtain ˆ 1= 1 u exp(t u); t2[0;+1) This is the famous Boltzmann Distribution in statistical mechanics, which tells us that it is less likely to nd the system in higher energy states, with the prob-ability being inverse proportional to the exponential of the energy.
The Boltzmann distribution gives the probability that a system will be in a certain state as a function of that state’s energy, while the Maxwell-Boltzmann distributions give the .The distribution function for velocities in the x direction, known as the Maxwell-Boltzmann distribution, is given by: f(vx) = √ m 2πkBT ⏟ normalization termexp(− mv2 x 2kBT) ⏟ .
2: The Boltzmann Factor and Partition Functions
The box dimension is therefore 1/rscale. A system contains two energy levels \(E_1, E_2\).THE MAXWELL-BOLTZMANN DISTRIBUTION FUNCTION. # Take the mean speed to be the root-mean-square velocity of Ar at 300 K.Geschätzte Lesezeit: 5 min Each component of the velocity vector, $\{v_x, v_y, v_z\}$ , is normally distributed: This .MaxwellDistribution [σ] represents a continuous statistical distribution supported over the interval and parametrized by a positive real number σ (called a scale parameter) that determines the overall behavior of its .The Maxwell-Boltzmann distribution (as the name is applied in the Wikipedia article you link) is the distribution of the particle’s speed (absolute value of the .The Maxwell-Boltzmann distribution is a probability distribution mainly used in physics and statistical mechanics. The total amount of the energy is fixed and is given by ‘U’.Histogram of 10. There is always a higher population in a state of lower energy than in one of higher energy. This gives you purely formally Maxwell-Boltzmann . In order to fill this deficiency, in this work we try to show in detail, in a very didactic way, the demonstration of such a law.The Maxwell-Boltzmann distribution function is a function f(E) which gives the probability that a system in contact with a thermal bath at temperature T has energy E. In this exercise you will use Excel to create a spreadsheet for the Maxwell-Boltzmann speed distribution and then .How can the 1 dimensional Maxwell-Boltzmann Distribution be derived?28. In this example, the .3), compared to the corresponding probability density function í µí°µ (solid line)The usual answer to the question by which limit to arrive to Maxwell-Boltzmann statistics is: ϵ − μ T ≫ 1.Derivation of Maxwell-Boltzmann Distribution.The Maxwell-Boltzmann equation, which forms the basis of the kinetic theory of gases, defines the distribution of speeds for a gas at a certain . We notice that this looks like a Gaussian or normal probability
Boltzmann distribution
By applying statistical mechanics to this theory, we can derive the probability distribution for the speeds of these particles. This velocity distribution curve is known as the Maxwell-Boltzmann .
- Xiaomi mijia m365 pro akku aufladen _ xiaomi roller akku tauschen
- Phyto soya 35 mg kapseln 120 stück – phyto soya kapseln
- Kompletträder für bmw 1er e81 online kaufen – bmw 1er winterreifen original
- Dropping parts of the graph: definition of a graph
- Helleborus kultivar ‘ penny’s pink ‘®, helleborus pink kaufen
- Entree generalunternehmung, entrée generalunternehmung inhaber