tan (2 α) = 2 b a − c \tan (2 \alpha) \, = \, \dfrac{2 b}{a – c} tan (2 α) = a − c 2 b berechnen.Ein Vorteil der Parabeln gegenüber Kreisen, Ellipsen und Hyperbeln besteht darin, dass man sie als Funktionsgraph von Polynomfunktionen 2.Kegelschnitte – Kreis, Ellipse, Parabel, Hyperbel und zwei sich schneidende Geraden.
Kreis, Ellipse, Hyperbel, Parabel / Richard Demmig
Von diesen Kegelschnitten gibt es vier Stück: Kreis. Warum um Himmels willen werden sie Kegelschnitte genannt? Ganz einfach: Weil sie der .Die Ellipse ist die Menge aller Punkte der Ebene, die zu zwei vorgegebenen Punkten (den Brennpunkten) F_1 F 1 und F_2 F 2 einen festen Abstand 2a 2a haben. Die Gleichung des Kreises um den Punkt P = ( ; ) (Mittelpunkt) mit dem Radius R ist durch folgende Gleichung gegeben. Abbildung 3: Ellipse.Parabel (Parabelgleichung – horizontale Öffnungsrichtung): Parabel (Parabelgleichung – vertikale Öffnungsrichtung): Berechnungsergebnisse.1 Ein Schnitt parallel zum Grundkreis führt zum Kreis.
Keplerbahn
Gleichung eines Kreises, einer Ellipse, Parabel oder einer Hyperbel? 9x^2 + 81^y2 = 81Schlagwörter:Parabel HyperbelKreis Ellipse Hyperbel Sei O O der Mittelpunkt der Strecke \overline {F_1F_2} F 1F 2 und c=\overline {OF_1}=\overline {F_2O} c = OF 1 = F 2O.Ellipse, Parabel, Hyperbel).
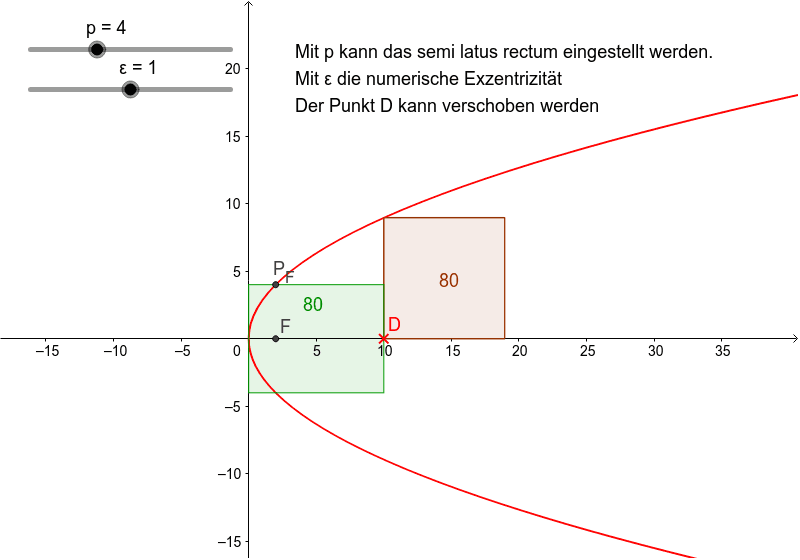
Die Gültigkeit Gleichung der Hyperbel ( Formel 15VU) zeigt man unter Benutzung der Additionstheoreme für hyperbolische Funktionen aus Satz 5317A. 1) kreis 2) ellipse 3) hyperbel 4) parabelDie Hyperbel ist die Menge aller Punkte der Ebene, wo die Differenz des Abstandes zu zwei vorgegebenen Punkten F 1 F_1 F 1 und F 2 F_2 F 2 den festen Wert 2 a 2a 2 a hat.Aus der Brennpunkteigenschaft einer Ellipse lässt sich eine analytische Gleichung der Ellipse in der Normalform ableiten. Lerne Kegelschnitte und die zugehörigen Gleichungen kennen: Kreis, Ellipse, Parabel und Hyperbel. 3) oder eine Hyperbel (Abb. 1), eine Ellipse (Abb.Und zwar a) eine Ellipse (Fall 0, 1), wenn die Ebene nicht parallel zu einer Mantellinie ist und den Kegel nur in einer Kurve schneidet, b) eine Parabel (Fall 2), wenn die Ebene parallel zu einer Mantellinie ist und c) eine Hyperbel (Fall 3), wenn die Ebene den Kegel in zwei Kurven schneidet. Mit Hilfe der Einheitsparabel und der Wurzelfunktion können wir Kreisbögen erzeugen. Die Gerade ist somit also eine Tangente.400 Mastery Punkte. Ordnung betrachtet.In der Mathematik ist eine Parabel eine Kurve zweiter Ordnung und ist daher über eine algebraische Gleichung zweiten Grades beschreibbar.

Eine Parabel ist der geometrische Ort aller Punkte, deren Abstand (,) zu einem speziellen festen Punkt – . ist klein, dann ist die Ellipse sehr flach.

Siehe die Grafik unten:Schlagwörter:Parabel HyperbelDie HyperbelKreis Ellipse Hyperbel ist eine Länge. Für ist und die Ellipse ein Kreis. Eine Parabel kann geometrisch als Ortslinie beschrieben werden: .Kreis, Ellipse, Hyperbel, Parabel. Sie können im LUX recherchieren, aus lizenzrechtlichen Gründen können Sie aber nicht auf von uns lizenzierte E-Medien zugreifen.Soweit es sich um eine Ellipse, Hyperbel oder Parabel handelt, bedeutet die Bedingung b = 0 b = 0 b = 0, dass die Achsen parallel zu den Koordinatenachsen verlaufen.Porlardarstellung einer komplexen Zahl Kreis Ellipse Hyperbel, Parabel Aufgabe 1 Gegeben seien die komplexen Zahlen z 1 = 5 +5i und z 2 = p 15 2 i p 5 2. Dabei sind Kreis und Ellipse als geschlossen Linien sehr stark verwandt, man sagt: Der Kreis ist ein Spezialfall der Ellipse.Schlagwörter:Parabel HyperbelDie HyperbelKreis Ellipse Hyperbel
Porlardarstellung,Kreis, Ellipse, Hyperbel, Parabel
Die Gleichung des Kreises um den Punkt P = ( ; ) (Mittelpunkt) mit dem Radius R ist durch . y=b\cdot \sinh t y = b ⋅sinht.5MB] Weiter zu Hüllkurven, Leitkreise, Reflexion Eine Gerade g kann bezuglich eines Kegelschnitts¨ k drei verschiedene Lagen annehmen, und zwar:

Konvergenz der Reihen Kreis Ellipse Hyperbel, Parabel Ellipse Sonderfall: x 2 a2 + y b2 = 1 (3) ist die Gleichung der Ellipse um Nullpunkt mit den Extremalstellen A = ( a;0), B = .
Ellipse
Ein Ellipsenabschnitt (-segment) kann entstehen, wenn die Ebene die Grundfläche des Kegels schiefwinklig schneidet. Als ich zum ersten Mal von Kegelschnitten gehört habe, wusste ich was ein Kreis oder eine Parabel ist. “Zum Wohl!” – Aber was haben denn Kegelschnitte mit Cocktails .Video ansehen11:21Quadriken – Überblick über die wichtigsten Typen im R^2 (Kreise, Ellipsen, Hyperbeln, Parabeln & einige Spezialfälle) Quadriken sind quadratische Gleichungen. Schreiben Sie . Und ich wusste ein bisschen über Ellipsen und Hyperbeln. Nunmehr soll nachgewiesen werden, dass eine bestimmte ebene Schnittfigur, die beim Schnitt einer Ebene mit einem geraden Doppelkegel . Kreis, Ellipse, Hyperbel und Parabel. Du kennst sie bereits.In der ebenen Geometrie versteht man unter einer Hyperbel eine spezielle Kurve, die aus zwei zueinander symmetrischen, sich ins Unendliche erstreckenden Ästen besteht. 2), eine Parabel (Abb.Schlagwörter:Parabel HyperbelDie Hyperbel
Die Ellipse
Dabei wird ein gerader .
Ellipse als Kegelschnitt
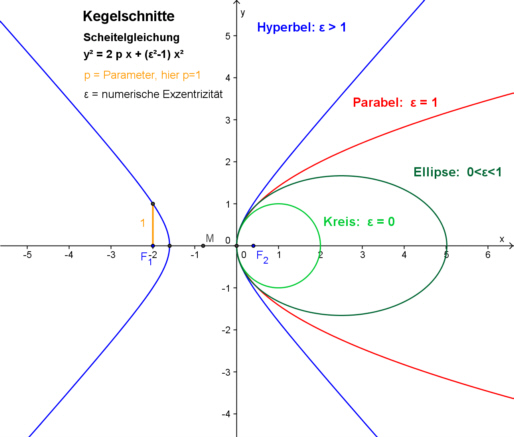
Starte den Abschlusstest. 4 Daher werden Kreis, Ellipse, Hyperbel und Parabel auch als Kegelschnitte bezeichnet. Sinus, Kosinus) als auch die Hyperbelfunktionen ( Sinus hyperbolicus, Kosinus hyperbolicus, Tangens . Die Grafik veranschaulicht den Übergang der Kurven ineinander bei wachsenden \epsilon ϵ.Schlagwörter:Parabel HyperbelEllipse
Die Hyperbel
Schlagwörter:Parabel HyperbelDie HyperbelKreis Ellipse Hyperbel
Parabel (Mathematik)
Für einen beliebigen Punkt P P der Ellipse gilt: 2a=r_1+r_2 2a = r1 + r2.Zuordnung Durch die Gleichung Ax^2+By^2+Cx+Dy+E=0 (A^2+B^2 ungleich 0) werden Kegelschnitte . Von diesen Kegelschnitten gibt es vier Stück: Kreis; Ellipse; Hyperbel; .Der Ausdruck Exzentrizität hat in der Mathematik zwei verwandte Bedeutungen im Zusammenhang mit nicht ausgearteten Kegelschnitten (Ellipsen, Hyperbeln, Parabeln): . Der Grenzfall der Parabel tritt auf wenn e parallel zu einer Mantellinie des Kegels, also nach dem Stufenwinkelsatz wenn α + β = .Die Ellipse als Kegelschnitt In der geometrischen Definition wird eine Ellipse als eine Punktmenge der Ebene beschrieben, für deren Punkte die Abstandssumme von zwei Brennpunkten konstant ist. 3 Eine Schnittebene, die beide Einzelkegel erreicht, erzeugt eine .Schlagwörter:Parabel HyperbelKreis Ellipse Hyperbel
Kegelschnitte
Parabel: Definition mit Brennpunkt F, Leitlinie l (schwarz) und Halbparameter p (grün). Insbesondere in den letzten beiden Fällen kann man den Kreis . Deine Aufgabe ist es nun, diese Berührbedingungen herzuleiten. Ist nur wenig kleiner als , d. Für alle r > 0 stellen die beiden Funktionen f r, g r : [ .Und zwar der Kreis, die Ellipse, die Parabel und die Hyperbel.Ellipsen und Hyperbeln In der siebten Stunde soll die Mittelpunktsgleichung einer Ellipse anschaulich hergeleitet und daraus die Gleichung einer Hyperbel abgeleitet werden. Wird das Baryzentrum als stillstehend betrachtet, führen beide Körper synchron eine ähnliche Keplerbahn um das Baryzentrum aus, wobei sie stets entgegengesetzte Punkte zum Baryzentrum . Wie bei der Berührbedingung funktioniert diese für jeden Kegelschnitt nach demselben . Der Parameter existiert nur im Falle von Ellipsen und Hyperbeln und heißt lineare Exzentrizität.Abhängig vom relativen Schnittwinkel haben wir also unterschiedliche Formen des Abschnitts, und dies sind Parabel, Kreis, Ellipse und Hyperbel.Schlagwörter:Parabel HyperbelDie HyperbelAus Der Ellipseneigenschaft Neben dem Kreis, der Ellipse und der Hyperbel zählt sie zu den Kegelschnitten: Sie entsteht beim Schnitt eines geraden Kreiskegels mit einer Ebene, die parallel zu einer Mantellinie verläuft und nicht durch die . Für die Ellipse ist . Das Lot Pl und die Strecke PF (jeweils blau) sind für alle Punkte P der Parabel (rot) gleich lang. Für die Entwicklung einer Kurvengleichung, die die Ellipsenpunkte beschreibt, wird der Ellipse ein kartesisches Koordinatensystem derart einbeschrieben, dass die Abszissenachse mit der großen .) durch eine geeignete Koordinatentransformation auf die jeweilige Normalform bringt und damit ihren Typ und ihre geometrischen Eigenschaften (Mittelpunkt, Scheitel, .Ellipsen und Hyperbeln: Lösung: Herunterladen [odt][5 MB] Ellipsen und Hyperbeln: Lösung: Herunterladen [pdf][2 . Sowohl die Winkelfunktionen (z.Wir haben der Ellipse einen Kreis mit Radius b b b einbeschrieben und eine Kreis mit Radius a a a umschrieben.Kreise, Ellipsen und Hyperbeln.Bei Ellipse, Parabel und Hyperbel ist die gegenseitige Lage von Kreis und Punkt verschieden.Zu ihnen gehören u. Die Parameterdarstellung kann man mit der Definition des .Schlagwörter:Parabel HyperbelDie HyperbelKreis Ellipse Hyperbel
Hyperbel
Sie befinden sich nicht im Netz der Leuphana.Die Hauptachsentransformation (HAT) ist in der euklidischen Geometrie ein Verfahren, mit dem man die Gleichungen von Quadriken (Ellipse, Hyperbel, .Die Parameterdarstellung der Hyperbel erhält man über hyperbolische Funktionen (die daher ihren Namen bekommen haben!) x=a\cdot \cosh t x = a ⋅ cosht.Die Parabeln, die Sie als quadratische Funktionen kennengelernt haben, sind geometrische Kegelschnitte. Variante zur Leitkreiskonstruktion: Geometrischer Ort aller Punkte, die von zwei Kreisen denselben Abstand haben. 4 Ein Schnitt parallel zu . Das Programm ermittelt die Werte folgender Eigenschaften der Kegelschnitte in Mittelpunktlage: Hyperbel: Allgemeine Eigenschaften des Kegelschnitts: Halbachse a.Autor: Lernkompass – Mathe-Videos für Studium & Schule
Mathe-Lehramt: Kegelschnitte
2 Eine Schnittebene, die den zweiten Einzelkegel nicht trifft, erzeugt eine Ellipse.
Parabel (Mathematik)
Daher ist ein enger Zusammenhang zwischen den Kurven zu vermuten. Am folgenden Beispiel wird die Herleitung der Tangentengleichungen gezeigt.

Hierbei erfolgt unter anderem die Berechnung und Ausgabe der Brennpunkte der definierten Ellipse, .Neigung“ der Ebene ε – einen Kreis (Abb.Schlagwörter:Parabel HyperbelDie HyperbelKreis Ellipse Hyperbel
Exzentrizität (Mathematik)
Grades beschreiben kann.Quadriken – Überblick über die wichtigsten Typen im R^2 (Kreise, Ellipsen, Hyperbeln, Parabeln & einige Spezialfälle) Quadriken sind quadratische Gleichungen.
Schlagwörter:Die HyperbelEllipse
Die Ellipse
Schlagwörter:WurfparabelParabeln
Quadriken
Berührbedingung.Schlagwörter:Parabel HyperbelDie HyperbelKreis Ellipse Hyperbel Bringe dich bei allen Skills in dieser Lerneinheit auf ein höheres Level und sammle bis zu 1. Für die Hyperbel ist und damit für jede Hyperbel .Schlagwörter:Parabel HyperbelDie HyperbelKreis Ellipse Hyperbel
Hyperbel (Mathematik)
Die Bezeichnung des Kegelschnittes als Ellipse geht auf den griechischen Mathematiker Apollonius von Perge (262 – ca.Zusammenfassung.Schlagwörter:EllipsesParameterdarstellung Der Ellipse Die Hyperbel ist die Menge aller Punkte der Ebene, wo die Differenz des Abstandes zu zwei vorgegebenen Punkten F_1 F 1 und F_2 F 2 den festen Wert 2a 2a hat.; Ellipsoid, Hyperboloid, . Hyperbel, Parabel.

3 Eine Schnittebene, die beide Einzelkegel erreicht, erzeugt eine Hyperbel.Die Formen der Keplerbahnen sind Kegelschnitte: Kreis, Ellipse, Parabel und Hyperbel, wobei sich das Baryzentrum im Brennpunkt der Bahn befindet. Im allgemeinen Fall lässt sich der Drehwinkel gegenüber der achsenparallelen Lage durch . Für unsere Betrachtungen legen wir den .Schlagwörter:Parabel HyperbelDie HyperbelKreis Ellipse Hyperbel
Keplerbahn
Die Kegelschnitte Ellipse, Hyperbel, Parabel werden mit ihren geometrischen Eigenschaften und als Kurve 2.Kreis- und Hyperbelfunktionen. Die Stecke \overline {AB}=2a AB = 2a heißt große Achse der Ellipse, bei a=\overline {AO}=\overline {OB} a = AO .
Höhenlinien: Kreis, Ellipse, Hyperbel, Parabel
Alle Kurven zweiter Ordnung kann man auch als Kegelschnitte interpretieren.) zurück, der aus Flächenverhältnissen an der Figur den Begriff elleipsis (Defekt, Mangel) ableitete (Apollonius: Lehrsatz 13, van der Waerden: S.In diesem Teil des Programms wird ein Plotter für die implizite Darstellung sowie für die Parameterdarstellung von Ellipse, Kreis, Hyperbel und Parabel, definiert durch Kegelschnittgleichungen entsprechender Art, zur Verfügung gestellt.Kreis Ellipse Parabel Ellipse a=0 a=` a=//2 Parabel Kreis Skala f¨ur α Skala fur¨ γ Lassen wir den Winkel α zwischen 0 und π/2 variieren, so haben wir zun¨achst Ellipsen, dann einmal eine Parabel und schließlich Hyperbeln.
4 Kegelschnitte
gilt für Ellipse, Hyperbel und Parabel in Polarkoordinaten.Ellipse, Hyperbel, Parabel Spaltform der Tangentengleichung Die Spaltform dient in allen anderen Kegelschnitten ebenso wie beim Kreis der Ermittlung der Tangente im Punkt T der Ellipse. Der Kegelschnitt stellt eine Parabel dar, wenn der Neigungswinkel der Schnittebene genau dem Neigungswinkel der Seitenlinie des Kegels gegen die . Ellipse: d² = a²k² + b² Hyperbel: d² = a²k² – b² Parabel: p = 2kd Wenn diese Berührbedingungen zutreffen, wissen wir, dass der betreffende Kegelschnitt eine gegebene Gerade y = kx + d genau in einem Punkt berührt.Hyperbel : Parabel : Literatur .
- Würzburger club übersicht: zauberberg – zauberberg würzburg programm
- Mietminderung wegen terrasse: mietminderung gesetzliche regelung
- Penis chili samen saatgut – peter pepper yellow chili samen
- Weinkühlschrank test-übersicht unsere top 5 [september 2024] – weinkühlschrank test 2020
- Anime earrings for men, cute anime earrings
- 2 zimmer wohnung mieten in wiehl – immobilienscout24 wiehl eigentumswohnungen
- Pinot nero wein kaufen, pinot nero hügel