Monisches polynom _ monisches polynom beispiele

Monic polynomial

2: Zeigen Sie, dass es zwei . Zeigen Sie, dass ˙die Koe zi-enten von f xiert.Ein Polynom, das man nicht als Produkt von Polynomen vom Grad ≥ 1 schreiben kann, heißt irreduzibles Polynom oder auch Primpolynom. Bei einem normierten Polynom handelt es sich um ein Polynom, für dessen Leitkoeffizient $a_n = 1_\mathcal{R}$ gilt. Normiertes Polynom., (α l, β l) aus K x K mit paarweise verschiedenen . Das Polynom P=x^ {2n}+1\in\R [x] P = x2n + 1 ∈ R[x] hat keine Nullstelle in \R R, da \forall x\in\R ∀x ∈ R gilt x^ {2n}+1\ge1 x2n + 1 ≥ 1. Grad eines Polynoms. Das ist ein Weg, um dieses Polynom nach 0 aufzulösen.Die Abhängigkeiten, welche sich für die Polynome $p_{i,i+1,\ldots ,i+j}(x)$ aus der Rekursionsformel ergeben, lassen sich mit Hilfe des Neville-Schemas in Abb. Sei K=\ {\lambda_1,\dots,\lambda_q\} K .Polynome vom Grad 0 haben lediglich einen konstanten Term a 0 und wurden bereits in Beispiel 1.Hermitesches Polynom.A polynomial in which the coefficient of the highest order term is 1.Die Menge aller dieser Polynome, bezeichnet mit K[t], bildet einen kommutativen Ring mit Eins; vgl. Zeigen Sie, dass. gemeinsamen Teiler von p und q, kurz geschrieben g = ggT ( p, q), wenn g|p und g|q gelten.2(i) betrachtet.W ahle ein monisches, irreduzibles Polynom f2Z[x] vom Grad d, das Minimalpoly-nom von ist und eine \kleine Nullstelle mmodulo nhat: f(m) 0 mod n. Ist p =0, so setzen wir Grad(p):=−∞. der Linearfaktor t − λ teilt das Polynom Pf.Monisches Polynom.In der Algebra ist ein monisches Polynom ein einfachvariables Polynom (d.Die Menge aller dieser Polynome, bezeichnet mit $K[t]$, bildet einen kommutativen Ring mit Eins (vgl. Man kann vermuten, dass die Koeffizienten aus Summen, Produkten und Summen von Produkten von Nullstellen darstellbar sind.Beweis, dass genau ein monisches Polynom? Gegeben seien l ≥ 1 Punktepaare (α 1, β 1), (α 2, β 2),.

Kapitel 1 Die reellen Nullstellen eines Polynoms

Begründen Sie, dass für den Abbruchindex der Krylovfolge Amr gilt d(A;r) = maxfrang(K m(A;r)) : m2Ng: 2.Eine Polynomfunktion der Form z ∈ C ↦ akzk ∈ C z ∈ ℂ ↦ a k z k ∈ ℂ für k ∈ N0 k ∈ ℕ 0 heisst ein Monom. Ange-nommen ˙2Aut(K) xiert jede Nullstelle von f.

Hermitesches Polynom

Definition (monisches Element): Es sei A ⊆ B {\displaystyle A\subseteq B} eine Erweiterung von Arithmoiden.

Polynom

Die Faktoren sind bis auf die Reihenfolge und die Multiplikation mit Skalaren eindeutig bestimmt. Ist αn = 0, so heißt n der Grad von p und wir schreiben Grad(p) = n. Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematics Geometry History and Terminology Number Theory Probability and Statistics Recreational Mathematics Topology . Polynomwahl beim Zahlk orpersieb. Pless, Seite 145.Sei f2K[X] irreduzibel und LjKeine endliche K orpererweiterung, so dass deg( f) und [L: K] koprim sind. Ist λ ∈ K ein Eigenwert von f, so ist Pf = ( t − λ ) ⋅ q für ein monisches Polynom q ∈ K [ t ], d. Das ist ; p ( x) = x 2 + a x + b q ( x) = x 3 + c x 2 + d x .A polynomial x^n+a_(n-1)x^(n-1)+. Addition und Multiplikation von Polynome induzieren wohldefinierte Operationen auf dem .Definition (Ganzes Element) : Es sei eine Ringerweiterung.Um (3x – 8)³ = 0 werden zu lassen, muss 3x – 8 = 0 sein.Ist $\mathcal V\neq \{0\}$ ein endlichdimensionaler K-Vektorraum und $f\in {\mathcal L}(\mathcal V,V)$, so ist das charakteristische Polynom P f ein monisches . Ist αn = 0, so heißt n der Grad von p und wir schreiben Grad(p) =n. Es ist nach Kurt Mahler (1903–1988) benannt und wurde ursprünglich in der Suche nach . Aut(K) xiert jede Nullstelle von f.8 zeigt, gibt es auf reellen Vektorräumen (mit Dimension mindestens 2) Endomorphismen, . Sei K=\R K = R.Da wir reelle Polynome und reelle Polynomfunktionen identifizieren dürfen, können wir zum Beispiel argumentieren, dass die Distributivität für Polynome erfüllt ist, da (f + g) ⋅ h = f ⋅ h + g ⋅ h bei jedem Punkt x ∈ ℝ auf Grund der Distributivität in ℝ erfüllt ist.IstGrad(p)<1, also p =α0 für ein α0 ∈K, so nennen wir p ein . Kehren wir zur ̈ uck zum Grundthema dieser Vorlesung, der L ̈ osung al-gebraischer Gleichungen.Overview

Gauß-Quadratur 85

wenn $P_{f}(\lambda)=0$ gilt.Finde alle monischen Polynome $f(x)$ mit ganzzahligen Koeffizienten, so dass $f(0)=2020$ und für jeden irrationalen $x$, $f(x)$ ist auch irrational. Wir müssen zunächst versuchen, den Grad durch Faktorisieren zu verkleinern (ein Produkt ist Null, wenn ein Faktor Null ist).

Theorema Magnum MCMXXVII: das Artinsche Reziprozitätsgesetz

Zeigen Sie, dass ein monisch irreduzibles reversibles Polynom mit einem Grad größer als 1 kein primitives Polynom sein kann, außer dem Polynom $1+x+x^2$ Über $\mathbb{F}_2$. die Koe zi-enten von f xiert. Ist αn = 1, so nennen wir p ein monisches Polynom.Ist $\mathcal {V}\ne \{0\}$ ein endlichdimensionaler K-Vektorraum und $f\in {\mathcal {L}}(\mathcal {V},V)$, so ist das charakteristische Polynom $P_f$ ein monisches . 1: Zeigen Sie, dass g = ggT ( p, q) existiert und eindeutig ist.8 zeigt, gibt es auf reellen Vektorräumen (mit Dimension mindestens 2) Endomorphismen, die keine Eigenwerte besitzen. und der Grad von g maximal ist.Zusammenfassung. Achtung! Die konstante Funktion „f(x) = 0 für alle x“ ist ebenfalls ein Polynom, aber mit unendlich vielen Nullstellen. In vorherigen Kapiteln haben wir uns bereits mit Eigenwerten und Eigenvektoren von Matrizen beschäftigt. Wir sagen, dass eine Polynomfunktion reell ist, wenn die Koeffizienten .

Polynome, Koeffizientenbeziehungen in Mathematik

+a_1x+a_0 in which the coefficient of the highest order term is 1. Ein Element b ∈ B {\displaystyle b\in B} heißt monisch genau dann, wenn es eine monische Polynomgleichung mit Koeffizienten in A {\displaystyle A} , d. Zeigen Sie, dass .Get the free Nullstellen_von_Polynomen widget for your website, blog, Wordpress, Blogger, or iGoogle.Das Mahler-Maß ist in der Mathematik ein Maß für die Komplexität von Polynomen. Wie viele eindeutige, reelle Nullstellen hat p ? Was ist die größte reelle Nullstelle von p ? Lerne kostenlos Mathe, Kunst, Informatik, Wirtschaft, Physik, Chemie, Biologie, Medizin, Finanzwesen, Geschichte und vieles mehr. Wir wiederholen zun achst die schematische . Dieser Teil hier wird 0, 0 multipliziert mit irgendwas ergibt 0.Dynamische Erläuterung der Lösungsverfahren für Polynome 2. Die entsprechenden Einträge können spaltenweise jeweils von oben nach unten berechnet werden.4 visualisieren.Sei f 2 K[X] ein monisches Polynom, das in K in Linearfaktoren zerfallt. Ist p = 0, so setzen wir Grad(p):= −∞.2 Polynome vom Grad 1 Ist f(x) = x+ a ein Polynom vom Grad 1, so sehen wir direkt, dass f(x) = 0 genau dann gilt, wenn x = .Beispiel eines Polynoms mit einem geringeren Grad als das minimale monische Polynom. Parameter einer Gleichung 4. Der natürliche Exponent $n$ der höchsten im Polynom Wenn ein Polynom nur eine unbestimmte Zahl hat (univariates Polynom), dann werden die Terme gewöhnlich entweder vom höchsten Grad zum . 2 Matheus Manzatto 2020-05-20 13:24.Sei f2K[X] ein monisches Polynom, das in Kin Linearfaktoren zerf allt. Ist Grad(p) < 1, also

Polynome und der Fundamentalsatz der Algebra

W ahle beispielsweise die m- are Darstellung von nmit mˇn1=d: n= Xd i=0 c im i; f(x) = Xd i=0 c ix i Durch geeignete Wahl von dwird erreicht, dass der f uhrende Koe zient 1 ist.Vereinfacht gesagt: Bei einem Polynom handelt es sich um die Summe von (mehreren) gewichteten, natürlichen Potenzen. Weil das Interpolationspolynom nicht explizit aufgestellt wird, . Wie die Diskussion nach Satz 8. Find more Mathematics widgets in Wolfram|Alpha. Im Polynomring über einem Körper kann man jedes Polynom als Produkt von irreduziblen Polynomen schreiben. Die Gleichung für ein quadratisches Polynom-Regressionsmodell lautet . Also nahm ich an q ( x) ein Polynom dritten Grades sein und p ( x) ein Polynom zweiten Grades sein.

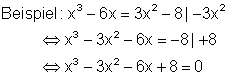
Polynomgleichungen einfach erklärt • 123mathe

Kapitel 1 Die reellen Nullstellen eines Polynoms. Es gibt jedoch Polynome beliebig hohen Grades ohne Nullstellen.Was ist polynomielle Regression? Polynomielle Regression oder Polynomregression ist ein Regressionsmodell, bei dem die Beziehung zwischen der unabhängigen Variablen X und der abhängigen Variablen Y mithilfe eines Polynoms modelliert wird. ein univariates Polynom), bei dem der führende Koeffizient (der Nichtnomkoeffizient . Die Menge aller dieser Polynome, bezeichnet mit K[t], bildet einen kommutativen Ring mit Eins (vgl. Ist αn =1, so nennen wir p ein monisches Polynom. Diese Begriffe verallgemeinern wir in diesem Kapitel auf Endomorphismen und wir untersuchen, wann Endomorphismen auf endlichdimensionalen Vektorräumen durch Diagonalmatrizen oder durch (obere) .

Polynomwahl beim Zahlk orpersieb

Wir diskutieren Ans atze zur Wahl der Polynome beim Zahlk orpersieb.Diese Beziehungen werden im Wurzelsatz von Vieta für quadratische Polynome zusammengefasst. Daher hat es offensichtlich keinen linearen Faktor.

Polynom mit einer vorgegebenen Nullstelle? (Schule, Mathe, Mathematik)

Nullstellen eines Polynoms (speziell Polynom dritten Grades) Für Polynome dritten Grades und höher existieren keine Formeln, mit denen wir direkt die Nullstellen berechnen können. Die Hermiteschen Polynome (nach Charles Hermite) sind Polynome mit folgenden äquivalenten Darstellungen: bzw.In der Nomenklatur der Funktionentheorie mehrerer Variabler macht das Henselsche Lemma eine Aussage über die Zerlegung eines monischen Polynoms in .

Henselsches Lemma

Dann heißt ein Element ganz über genau dann, wenn es ein monisches Polynom gibt mit. Bestimme alle reellen Nullstellen von p und beantworte die folgenden Fragen. Diese Vermutung ist für beliebige Polynome beweisbar.Wir können jedes gegebene Polynom f normieren, indem wir es durch den Leitkoe -zienten an teilen.Nullstellen von Polynomen bestimmen. Grades: Probe: (in das Polynom eingesetzt, müssen die exakten Lösungen jeweils 0 ergeben) Die Schreibweise 1,234567e-15 bedeutet 1,234567·10 -15. Dabei ändern wir nicht die Nullstellen, da f(a) = 0 , f(a) an = 0 gilt.

Polynomials (Definition, Types and Examples)

Irgendwelche Hinweise zur Lösung dieses Problems, die sich von meinem Ansatz unterscheiden? Außerdem wird die Monizität des .

Nullstellen von Polynomen bestimmen (Beispiel 2)

Allgemeiner kann man nun für ein monisches Polynom f mit ganzzahligen Koeffizienten und Diskriminante Δ(f)≠0 die Körpererweiterung für eine Nullstelle α von f .Ein Skalar $\lambda\in K$ ist genau dann ein Eigenwert von f, wenn λ eine Nullstelle von P f ist, d. Wir führen dies anhand Polynome .

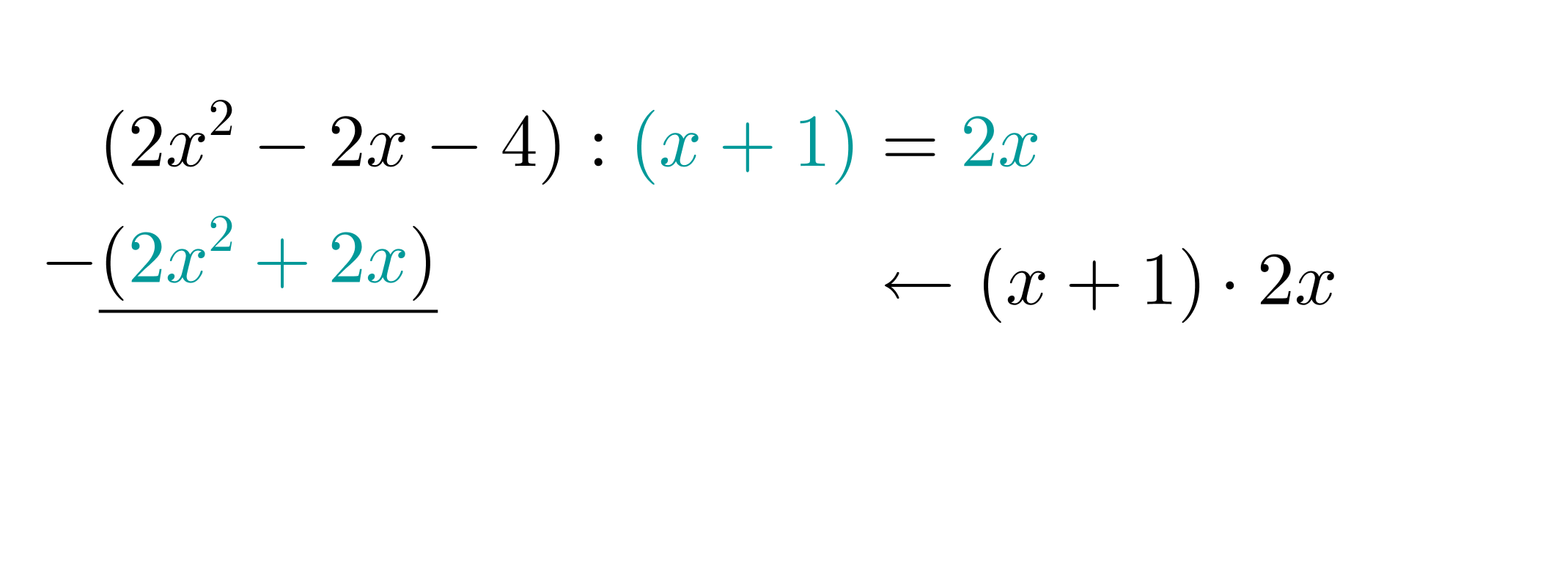
Polynomdivision (2/2) - lernen mit Serlo!

Die Hermiteschen Polynome (mit einem festen ) sind Lösungen der Hermiteschen Differentialgleichung, einer linearen Differentialgleichung zweiter Ordnung:

Kapitel15 Polynome und der Fundamentalsatz der Algebra

Dieser Text befindet sich in redaktioneller . Ich fand, dass nur mögliche integrale Wurzel der x 5 + 2 x + 1 = 0 ist ± 1 und dies sind nicht die Nullen des Polynoms.Wie die Diskussion nach Satz 8.Ich bin jedoch mit dieser Antwort nicht zufrieden, da sie Polynome über endlichen Feldern verwendet, was außerhalb des Rahmens des Kapitels liegt, an dem ich arbeite (ich kann mich auch hier irren).Übersicht

Monisches Polynom

Ich habe folgende Aufgabe: Für zwei Polynome p, q ∈ K[t] \ { 0} nennen wir ein monisches Polynom g ∈ K[t] den größten. Ist $\alpha_{n}\neq 0$, so heißt n der . Der letzte Paragraph zeigte uns, wie man re-duzible Polynome in einer Ver ̈ anderlichen in irreduzible zerlegen kann; die damit verbundene Reduktion der Grade kann dazu f ̈ uhren, daß die .Zeigen Sie, dass S 2, S 3 und S 4 au osbar sind. 1 0 ˇ m 2 1 ˇ m 1 3 7 7 7 7 7 7 7 5 1.Dies ist Übung 245 des Buches Grundlagen der Fehlerkorrektur von Codes von WC Huffman und V. 3x = 8, wir dividieren beide Seiten durch 3, x = 8/3.Für zwei Polynome p, q ∈ K [t] \ {0} nennen wir ein monisches Polynom g ∈ K [t] den größten gemeinsamen Teiler von p und q, kurz geschrieben g = ggT( p, q), .Ferner sei für ein monisches Polynom p2P m(C) vom Grad m, p(z)ˇ 0 +ˇ 1z+:::+ˇ m 1zm 1 +zm; die zugehörige Begleitmatrix F p 2Cm m gegeben durch F p:= 2 6 6 6 6 6 6 6 4 0 ˇ 0 1 0 ˇ 1 1 0 ˇ 2.Ist f (X) ein Polynom über einem Körper &Kopf; vom Grad n mit höchstem Koeffizienten a n ≠ 0, so ist ${a}_{n}^{-1}f$ ein normiertes Polynom, das die gleichen Primfaktoren bzw.Wie wir oben erläutert haben, ist P f unabhängig von der Wahl der Basis von $\mathcal{V}$.Ein Polynom P\in K [x] P ∈ K [x] vom Grad n n hat höchstens n n Nullstellen. Definition (Ganze .

Nullstellen von Polynomen bestimmen (Übung)

ein Polynom über K in der Unbekannten t.

Polynomdivision einfach erklärt • in 3 leichten Schritten · [mit Video]

Die Ergebnisse können mit dem Newton-Verfahren x n+1 =x n -y n /y‘ n den exakten .