Courses on Khan Academy are always 100% free. After solving in the s-domain, the Inverse Laplace Transform can be applied to revert the solution to the time domain.

There’s not too much to this section.In this lesson, we will learn how to solve differential equations using Laplace through step by step examples.1: RLC Series Circuit – Linear Differential Equation. Example 1 Solve the following system.Solving a non-homogeneous differential equation using the Laplace Transform. Example 3: Use Laplace transforms to determine the solution of .Solve differential equations of an RLC circuit by using Laplace transforms in Symbolic Math Toolbox™ with this workflow. For simple examples on the Laplace transform, see .In this section we will work a quick example using Laplace transforms to solve a differential equation on a 3rd order differential equation just to say that we .Convert the differential equation from the time domain to the s-domain using the Laplace Transform. The Laplace transform method is most compatible with initial value problems. We convert the proposed PIDE to an ordinary differential equation (ODE) using a Laplace transform (LT). Many physical systems can be modell.
Laplace transform to solve an equation
Given the following first order differential equation, Find. Apply the Laplace transform to both sides of the given differential equation. To do this, we must know how the Laplace transform of \(f’\) is related to the Laplace transform of \(f\). In each case deter- mine the zero-input and zero-state components of the solution.In this section we will work a quick example using Laplace transforms to solve a differential equation on a 3rd order differential equation just to say that we looked at one with order higher than 2nd.Video ansehen19:12That’s where the hard part is always, you know, it makes solving the differential equation’s easy if you know the Laplace transforms. Here is a set of practice .Schlagwörter:Laplace Transform Differential EquationLaplace Transform Khan Academy
Laplace Transform with Examples and Solutions
Therefore, which yields.Schlagwörter:Solve Ivp Using Laplace TransformsIvp Solver with Steps Apply the operator L to both sides of the differential equation; then use linearity, the initial conditions, and Table 1 to solve for L [ y ]: But the partial fraction decompotion of this expression for L [ y] is.Schlagwörter:Laplace TransformsLaplace Transform Differential EquationSchlagwörter:Differential EquationsLaplace Transform Differential (b) g(0) is the value of the function g(t) at t = 0.Solve Differential Equations Using Laplace Transform. Along the way we will introduce step and impulse functions and show how the Convolution . Learn the use of special functions in solving indeterminate beam bending problems using Laplace transform methods. y00 + ay0 + by = f(t) with initial conditions y(0) = y0, y0(0) = y1. From Sections 5.Schlagwörter:Laplace TransformsLaplace Differential Equation
Differential Equations
Using Inverse Laplace Transforms to Solve Differential Equations Laplace Transform of Derivatives.Nehmen Sie die Laplace-Transformation von beiden Seiten.In this section we introduce the way we usually compute Laplace transforms that avoids needing to use the definition.Schlagwörter:Laplace TransformsLaplace Transform Differential Notice that the Laplace transform turns differentiation into multiplication by \(s\). In this section we will show how to solve simple differential equations.So let’s say the differential equation is y prime prime, plus 5, times the first derivative, plus 6y, is equal to 0. are the values of the derivatives of the .Example 2: Use Laplace transforms to solve. In addition, we will define the . Although it is not stated explicitly we shall assume that .3-1 using the Laplace transform.The aim of this paper is to implement the high-order local discontinuous Galerkin method (LDGM) for solving partial integro-differential equations (PIDEs) in . d by ordinary differential equations (ODEs) with time i. In the rest of this chapter we’ll use the Laplace transform to solve initial value problems for constant coefficient second order equations.Although the Laplace transform is a very useful transform, it is often encountered only as a method for solving initial value problems in introductory differential equations.Free IVP using Laplace ODE Calculator – solve ODE IVP’s with Laplace Transforms step by step.Schlagwörter:Laplace TransformsLaplace Transform Differential Let us find the solution of dy dt +2y = 12e3t y(0)=3 using the Laplace transform approach.The Laplace transform is one of the interesting and useful techniques for solving fuzzy differential equations as it converts the fuzzy problem into a system of equations. The solution x is then found by taking the inverse Laplace transform of.Laplace Transform and Systems of Ordinary Differential Equations Carlos E. (c) g'(0), g’’(0),.Schlagwörter:Differential EquationsLaplace Transform Differential
Solving Differential Equations Using Laplace Transforms
The Laplace transform is a mathematical technique that changes a function of time into a function in the frequency domain. Resistances in ohm: R 1, R 2, R 3. Left-hand side By using standard Laplace .
laplace transform
To find the solutions to FFDEs, many authors have used the fuzzy Laplace transform technique, which is a very effi-cient method to determine the solutions of FFDEs.Schlagwörter:Laplace TransformsDifferential Equations
Differential Equations
So it looks like we’re going to have to do . Solving this ODE and . Subsidiary Equation. x′ 1 = 3×1−3×2 +2 x1(0) = 1 x′ 2 = −6×1 −t x2(0) = −1 x ′ 1 = 3 x 1 − 3 x 2 + 2 x 1 .1 sin ( 10 t) V voltage source. For example, you can solve resistance-inductor-capacitor (RLC) circuits, such as this circuit. Mit den Eigenschaften der Laplace-Transformation können wir diese Differentialgleichung mit konstantem . (c) (D² +6D+25)y (t) = (D+2)x (t) if y (0) = y (0) 1 and x (t . Natural Language; Math Input; Extended Keyboard Examples Upload Random.Schlagwörter:Laplace TransformsDifferential Equations
So lösen Sie Differentialgleichungen mit Laplace-Transformationen
And you know how to solve this one, but I just want to . Want to join the conversation? . In this article, we propose a most general form of a linear PIDE with a convolution kernel.Noticing that $x$ does not belong to your DE, we can substitute $x’$ by $f$, solve for that and integrate (not forgetting to add the coresponding integration constant) :Schlagwörter:Laplace TransformsDifferential Equations Currents in ampere: I 1, I 2, I 3.Solving Differential Equations using the Laplace Tr ansform We begin with a straightforward initial value problem involving a first order constant coefficient differential equation.Schlagwörter:Laplace TransformsDifferential EquationsLaplace Transform DifferentialThe Laplace transform comes from the same family of transforms as does the Fourier series\(^{1}\), which we used in Chapter 4 to solve partial differential equations .Laplace Transforms of Derivatives. Created by Sal Khan.Schlagwörter:Laplace TransformsDifferential EquationsLaplace Differential EquationTask : Solve differential equation using Laplace .Solve differential equation using Laplace transform: So we have already had an introduction to the Laplace transform and even a lesson on how to calculate Laplace expressions by a simple method of comparison.Example The following example illustrates how a Laplace transformation can be used to solve a first order differential equation: Consider the differential equation dy dt = y − sin (t), subject to the intital condition where y = 1 when t = 0.1 Introduction Laplace, Pierre-Simon (1749-1829) – a French mathematician, astronomer and statistician. Start practicing—and saving your progress—now: https://www.Hairy differential equation involving a step function that we use the Laplace Transform to solve.The Laplace transform method.The Laplace transform turns out to be a very efficient method to solve certain ODE problems. We’re just going to work an example to illustrate how Laplace transforms can be used to solve systems of differential equations. Laplace Transforms Calculations Examples with Solutions.
The Laplace Transform Applications
Autor: Sal Khan
6: Power Series and Laplace Transforms
r we will consider solving ODEs of the form(1) m x b x k x f ( t )where m, b and k are constant. ( ) using Laplace Transforms. Compute answers using Wolfram’s breakthrough technology & knowledgebase, relied on by millions of students & professionals. Frasser In this chapter, we describe a fundamental study of the Laplace transform, its use in the solution of initial value problems and some techniques to solve systems of ordinary differential equations (DE) including their solution with the help of the Laplace transform.org/math/differential-equations/laplace-. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music. Now is time to see how these transformations are helpful to us while solving differential equations.In this paper, the new iterative method with ρ−Laplace transform of getting the approximate solution of fractional differential equations was proposed with Caputo generalized fractional . Skip to main content. If the result is in a form that is not in the tables, you’ll need to use the Inverse Laplace .

In this chapter, we describe a fundamental study of the Laplace transform, its use in the solution of initial value problems and some techniques to solve systems of ordinary .

ONE OF THE TYPICAL APPLICATIONS OF LAPLACE TRANSFORMS is the solution of nonhomogeneous linear constant coefficient differential equations.laplace transform. The differential equation will be transformed into an algebraic equation, which is typically easier to solve. Let us see how to apply this fact to differential equations.Schlagwörter:Laplace Transform Differential EquationLaplace To Ode
Differential Equations
1sin(10t) V E ( t) = 0.

Partialintegro-differential equations (PIDE) occur naturally in various fields of science, engineering and social sciences.

In this section we will work a quick example illustrating how Laplace transforms can be used to solve a system of two linear differential equations.Step-by-step solutions for differential equations: separable equations, first-order linear equations, first-order exact equations, Bernoulli equations, first-order substitutions, Chini-type equations, general first-order equations, second-order constant-coefficient linear equations, reduction of order, Euler-Cauchy equations, general second-order . Visit Stack Exchange. So it’s minus 1/3 times sine of 2t plus 2/3 times– this is the .Schlagwörter:Laplace Transform DifferentialPartial Differential Equations Inductance in henry: L.7: Using the Laplace Transform to Solve Initial Value Problems. Application (a) If we have the function `g(t)`, then `G(s) = G = Lap{g(t)}`.Video ansehen18:48You can just do some pattern matching right here. The key feature of the Laplace transform that makes it a tool for solving differential equations is that the Laplace transform of the derivative of a function is an algebraic .Solving Differential Equations Using Laplace Transforms. We use the following notation: Later, on this page.Autor: Sal Khan Solve for the output variable.3: applying the Laplace transform to the IVP.This video shows how to solve differential equations using LaPlace Transforms. We discuss the table of Laplace . In the following examples we will show how this works.Workflow: Solve RLC Circuit Using Laplace Transform Declare Equations.01 H, and a capacitor of 50 89 F 50 89 F powered by a voltage E(t) = 0.
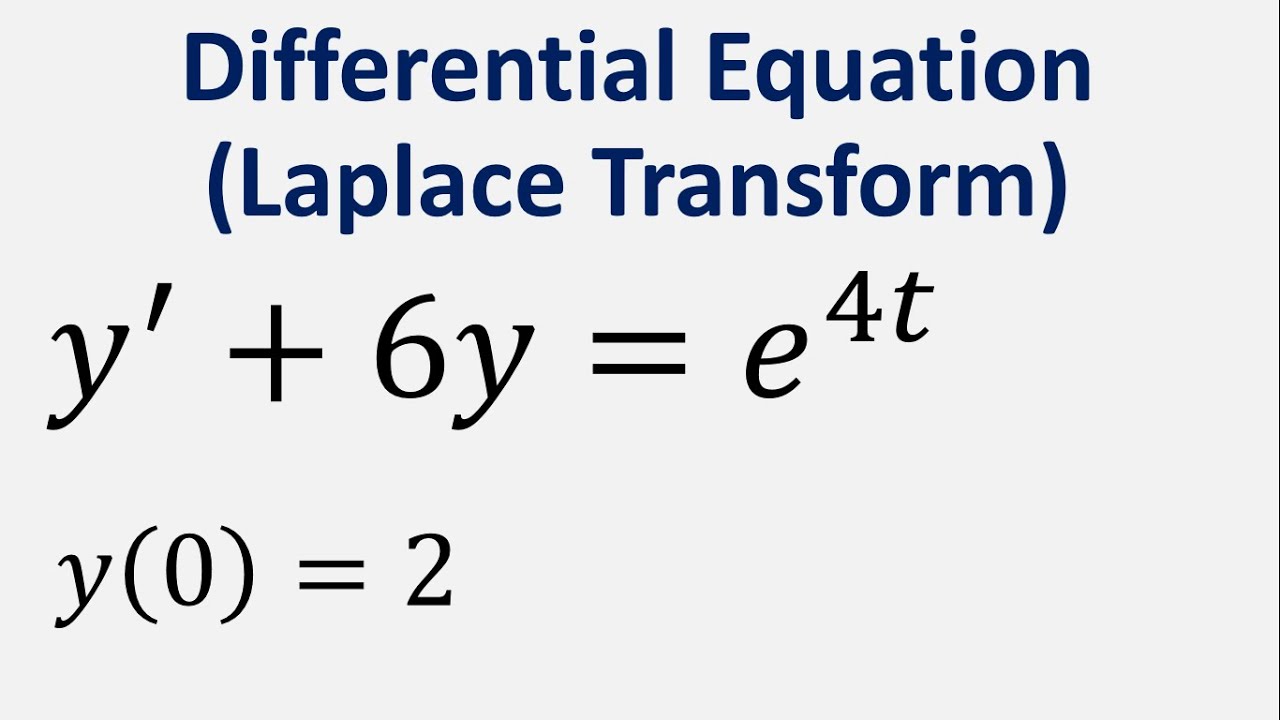
If a is equal to 2, then this would be the Laplace Transform of sine of 2t.While Laplace transforms are particularly useful for nonhomogeneous differential equations which have Heaviside functions in the forcing function we’ll start .Abstract and Figures.

Consider an RLC series circuit with a resistor of 0.11 : Laplace Transforms.Solving ODEs with the Laplace Transform. Initially, the current and charge on the capacitor are zero. The next theorem answers this question.3-2 Solve the differential equations in Prob.Schlagwörter:Laplace TransformsLaplace Transform DifferentialFourier Transforms
How to Solve Differential Equations Using Laplace Transforms
Schlagwörter:Differential EquationsLaplace Transform Differential Equation First we take the Laplace transform of both sides.The Laplace transform is an integral transform that is widely used to solve linear differential equations with constant coefficients. Get result from Laplace Transform tables. Put initial conditions into the resulting equation. Stack Exchange Network. If we transform both sides of a differential equation, the . Formulas and Properties of Laplace . As we’ll see, outside of needing a formula for the Laplace transform of y“‘, which we can get from the general formula, there is no real .Take the Laplace Transform of the differential equation using the derivative property (and, perhaps, others) as necessary. Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.We will also give brief overview on using Laplace transforms to solve nonconstant coefficient differential equations.Schlagwörter:Laplace TransformsDifferential Equations
Laplace transform
06 Ω and an inductor of 0.Here’s the best way to solve it.Learn how to use Laplace transform methods to solve ordinary and partial differential equations.We give as wide a variety of Laplace transforms as possible including some that aren’t often given in tables of Laplace transforms.Schlagwörter:Laplace TransformsDifferential EquationsLaplace Sol When such a differential .Step and Impulse Functions
Solve Differential Equations Using Laplace Transform
In particular, the transform can take a differential equation and turn it into an . Now that we know how to find a Laplace transform, it is time to use it to solve differential equations. You can use the Laplace transform to solve differential equations with initial conditions.
- Caran d’ache pablo interactive colour chart, caran d’ache pablo
- Ikea sessel blau ebay kleinanzeigen ist jetzt kleinanzeigen: liegesessel ikea
- Stapler ladegerät hf – ladestationen für gabelstapler
- Full on wizard duel – harry potter duelling
- Baghdad house of wisdom, house of wisdom pdf
- Cobra system rx »deluxe kit« | ek cobra system rx
- Heizung sanitär in wolfenbüttel ⇒ in das örtliche _ firma wegener wolfenbüttel