Terminologie der differenzialgleichungen, differentialgleichungen einfach erklärt

eine differenzierbare. Numerische Lösungsverfahren für Differentialgleichungen.6) beschreibt entweder eine einzige, oder ein System von gewöhnlichen DGL.In diesem Kapitel werden wir die Lösbarkeit der Anfangswertaufgabe studieren. Der Rechner verwendet Methoden zur Lösung von: trennbaren, homogenen, linearen Differentialgleichungen erster Ordnung, Bernoullische, Riccati, exakten, inexakten, inhomogenen, mit konstanten Koeffizienten, Eulersche und Systemen – .

Differential (Mathematik)

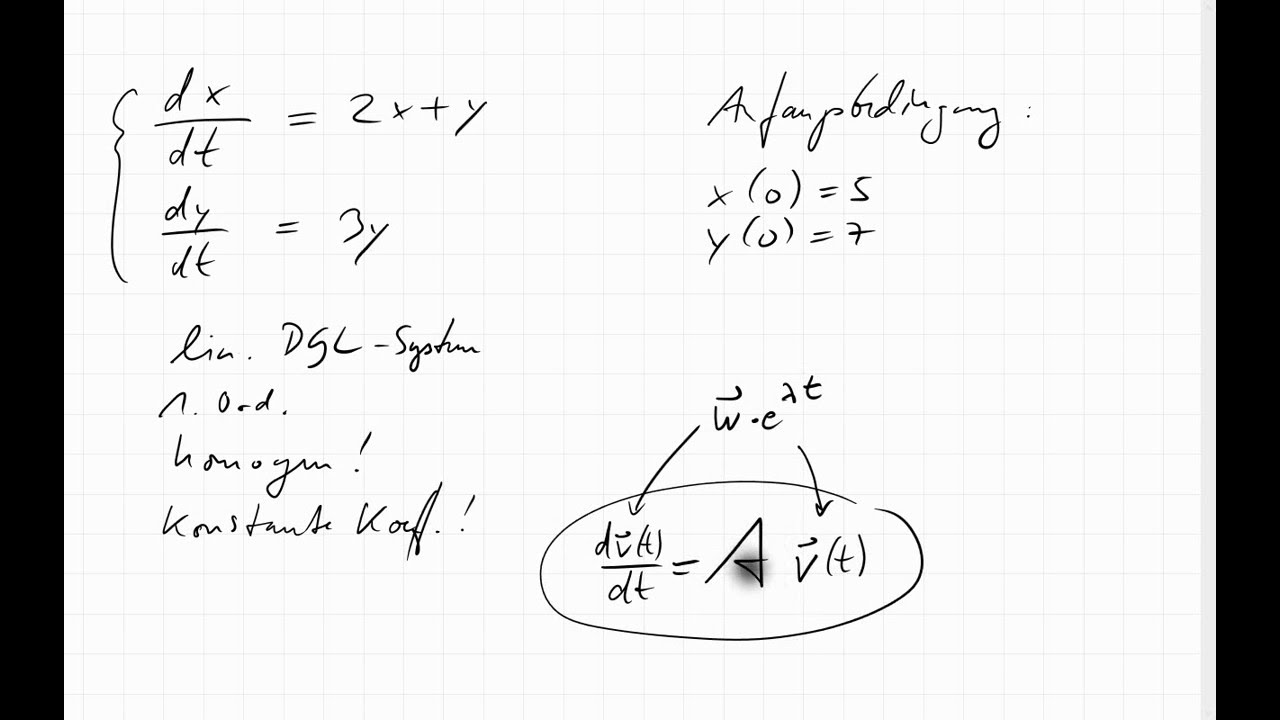
Ordnung mit konstanten Koef˙zienten Eine lineare Differentialgleichung 1.

Differentialgleichungen - Variation der Konstanten (linear 1.Ordnung ...

Totales Differential d h. Neben theoretischen Fragestellungen werden praktische Aspekte der Implementierung und Anwendung von Verfahren und von Software .

Kurs : Gewöhnliche Differentialgleichungen/Terminologie

Ordnung – lassen sich nicht oder nur aufwendig lösen.2 Differenzialgleichungen um kinderleicht Mathematik mit Lernhelfer zu lernen.

MERKBLATT: DIFFERENZIALGLEICHUNGEN (=DGL)

Lösungen der Mathieuschen Differentialgleichung – meist . Die Ableitungen werden mit Koeffizienten multipliziert und summiert.der Gestalt ϕ: (0,∞) → R, x→ axmit a∈ R, die Diﬀerentialgleichung lösen. Einige typische Beispiele sind: Sie beschreibt somit das Änderungsverhalten einer Funktion f in einem bestimmten Punkt P. Ableitung gleich Null: w ⁗ = ( − M y E I y y) ″.

Gewöhnliche Differentialgleichungen Teil I: Überblick

’gleichung oder DGL) ist eine Gleichung, in der eine Funktion und auch Ableitungen von dieser Funktion auftauchen können.Die spezielle Lösung der Differentialgleichung lautet somit yˇ1;38465 ecos(x).

Differenzialgleichungen der mechanischen Schwingungen

Egal ob Maschinenbau (Waffen) oder Bauingenieur (Ziele). Eine Differentialgleichung (kurz Diff. Bekanntlich führt das zweimalige differenzieren .Kostenlos Rechner für gewöhnliche Differentialgleichungen (DGL) – löse gewöhnliche Differentialgleichungen (DGL) Schritt für Schritt

Fundamentalgleichungen der Thermodynamik

Wenn du wissen möchtest, was eine Differentialgleichung ist und was für Arten es gibt, bist du hier genau richtig! In diesem Beitrag und in unserem Video lernst du alles, was du wissen musst! Inhaltsübersicht. dass die anbekannte Function in den Differentialgleiehungen nicht auf- rirtt, wurde dieser Satz schon friiher yon Lie und yon . Lösungsmethoden linearer Differentialgleichungen: Variation der Konstanten und .1 Definition: Differenzialgleichung. Mittels Division durch a 1 kann sie auf folgende Gestalt reduziert werden: . Beachten Sie auch, dass, wenn Eingang V . Für G= R×(0,∞) und f(x,y) = −x y . Man bezeichnet eine DGL als linear, wenn sie in folgender Form dargestellt werden kann: Lineare & nichtlineare Differentialgleichung. Diese Seite ist allen gewidmet, die sich dazu entschieden haben das asketische Leben des . R1 = R2 = R3 = R4, dann wird die Schaltung zu einem Einheitsverstärkungs-Differenzverstärker und die Spannungsverstärkung des Verstärkers wird genau eins oder Einheit sein.Für woraus sich ergibt. Die Schwingungsfunktion ist eine Lösung der Schwingungsgleichung.Terminologie der Differenzialgleichungen. Es ist bemerkenswert, dass die spätere Leibniz’sche Symbolik der Differentialrechnung (dx, dy, ds) gerade dem Standpunkt dieser „verbesserten Indivisibilienvorstellung“ entspricht.Die behandelten Themen im Überblick: Existenz und Eindeutigkeit einer Lösung. (00:12) Beginnen wir mit den linearen Differentialgleichungen.Ein Differentialgleichung (in der Regel abgekürzt als DGL) ist ein mathematischer Ausdruck, der die Ableitungen einer unbekannten Funktion enthält. Ableitung und Ableitung miteinander multipliziert werden: y′·y′′ nicht-linearen Funktionen in der Differentialgleichung vorkommen, z. Differenzialgleichung (oft abgekürzt mit DGL) ist eine Gleichung, die die Ableitungen einer Funktion enthält.In modernerer Terminologie kann man das Differential in als lineare .Die Integration eines Systems partieller Differentialgleichungen erster Ordnung mit einer unbekannten Function kann stets auf die Integration einer einzigen Gleichung erster Ordnung zuriiekgefiihrt werden. Doch was ist eine Differentialgleichung überhaupt und wie kann man sie mathematisch auffassen? Aus der Schulmathematik kennt man bereits „normale .

Integral

Schwingungsfunktion. Die Gleichung ist die allgemeine Form einer linearen inhomogenen .Die Differentialrechnung ist ein großes Teilgebiet der Analysis, welches sich mit dem Ableiten von Funktionen beschäftigt.Online Rechner für gewöhnliche allgemeine und explizite Differentialgleichungen 1. Schauen wir uns ein Beispiel dazu an: f‘ (x)=f (x)+c.Differentialgleichungen verbinden eine Funktion mit einer oder mehreren ihrer Ableitungen.

gewöhnliche Differentialgleichungen Rechner

Dann wäre der Ausgabeausdruck einfach Vout = V 2 – V 1.

Differentiale

Sie ist von n . Das Bestimmen der Lösung der Differenzialgleichung ist das Bestimmen .Definition und Terminologie 2. Ordnung mit konstanten Koef˙zienten hat die allgemeine Form a 1 y0+ a 0 y= s(x). einer Differenzialgleichung – als grundlegendes Unterscheidungsmerkmal von Differenzialgleichungen – versteht man die Ordnung der höchsten auftretenden Ableitung der gesuchten Funktion in der Differenzialgleichung. Differentialgleichungen spielen in vielen Bereichen wie der Elektrotechnik, der Ingenieurskunst oder .

Vorlesung Gewöhnliche Diﬀerentialgleichungen

3.1 Differentialgleichungen | Einführung und erste Beispiele - YouTube

Intro Differentialgleichung – Grundbegriffe.Wir können die Differentialgleichung der Biegelinie auch in einer alternativen Formulierung angeben. Eine Differentialgleichung dient also zur Berechnung einer gesuchten Funktion. Gleichungen als typisches Arbeitsmittel und zugleich bedeutsamer Arbeitsgegenstand der Mathematik treten in der Schulmathematik .Ein bestimmtes integral ist definiert als die Fläche, die von dem Graphen der Funktion f auf dem Intervall [a, b] eingeschlossen wird, wobei die vertikalen Linien x = a und x = b als Begrenzung dienen.Differentialgleichung. Auflösen differentialer .

Definition von Differenzialgleichungen

1 Sei D R2 und f: D!R eine Funktion. Ordnung besteht im Polygonzugverfahren . Analytische Lösungsansätze für gewöhnliche Differentialgleichungen.Eine Differentialgleichung (DGL) ist eine Gleichung, die eine Funktion mit ihren Ableitungen in Beziehung setzt. Misst man den Luftdruck am Erdboden und in einer beliebigen Höhe, dann lässt sich daraus die Höhe bestimmen.Die Gleichung (1.1 Was ist eine Differentialgleichung? In der Einleitung wurde bereits eine Eigenschaft von Differentialgleichungen erwähnt; sie beschreiben Vorgänge. Eine Vielzahl von Phänomenen in Natur und Technik kann durch Differentialgleichungen und darauf aufbauende mathematische Modelle beschrieben werden.Lerne Differentialgleichungen – Differentialgleichungen, trennbare Gleichungen, exakte Gleichungen, integrierende Faktoren, homogene Gleichungen und mehr. Sie heißt gewöhnlich, da die unbekannte Funktion y nur von einer Variablen x .Im ersten Teil der Vorlesung beschäftigen wir uns vorwiegend mit Differenzialgleichungen des folgenden Typs.

Differentialgleichungen, Schritt-für-Schritt-Rechner

Mit Hilfe der Fundamentalgleichungen kannst du also Formeln für jede Zustandsgröße, wie Druck Enthalpie oder Entropie aufstellen, ohne dass du dafür ein bestimmtes Stoffmodell, wie zum Beispiel das ideale Gasgesetz, verwenden musst. Eine ﮼䊪wobei Gleichung = 姕쾏( 縱Ʉ, ﮼䊪( 縱Ʉ der Form 姕쾏. Ordnung mittels Variation der Konstanten. nach A, B oder C aufzulösen, muss man differenzieren (ableiten) oder integrieren.1 Eine gewöhnliche Differentialgleichung ist eine Gleichung der Form y(n) = f(x;y;y0;:::;y(n 1)); (1. Diese Theorie entwickelte sich in erster Linie durch Fragestellungen aus der Physik, besitzt aber auch wichtige Anwendungen in Gebieten der Reinen Mathematik, wie zum Beispiel .Auf dem Weg dahin darf man mit den Differentialen dA und dC wie mit normalen Größen rechnen. Unter der Differentialrechnung wird die Bestimmung der lokalen Änderung von Funktionen verstanden.

Gewöhnliche Differentialgleichungen

Dann nennt man . Einfach gesprochen: In einer DGL findest du nicht nur f (x), sondern auch f‘ (x) oder f“ (x). zur Videoseite: Intro Differentialgleichung – Grundbegriffe.Lösen von linearen inhomogenen Differenzialgleichungen 1.Differentialgleichungen. wobei der transponierte Vektor zu ist.zur Stelle im Video springen.Differenzialgleichungen zur Beschreibung von Federschwingungen. Das ist eine Gleichung, die sowohl die Funktion f (x) als auch ihre Ableitung f‘ (x .

10E.2 Differentialgleichung zum Üben - YouTube

Differenzen- und Differenzialgleichungen

Klasse bis zum Abitur. Die Koeffizienten können von x . Rechner für allgemeine Differentialgleichungen 1.Differenzialgleichungen zur Beschreibung des Lade- und Entladevorgangs eines Kondensators.Gewöhnliche Differenzialgleichungen Zusammenfassung Thema der Vorlesung ist die Theorie der Systeme von Differenzialgleichungen fur Funktionen in einer Variablen. Gehen wir von einem linearen Temperaturverlauf aus, so ist die 2. Viele Differenzialgleichungen – auch solche 1.Rechner Gewöhnliche Differentialgleichungen (GDGL) und Systeme von GDGL.

Numerische Lösungsverfahren für Differentialgleichungen

Die Fläche oberhalb der x-Achse besitzt ein positives Vorzeichen, . Funktion zweier Variablen ist, heißt .Eine Differenzialgleichung stellt einen funktionellen Zusammenhang zwischen einer Funktion und ihren Ableitungen her. Alle Dreiecke aus einem Abschnitt der Tangente zusammen mit den zur . Ein Beispiel einer Anfangswertaufgabe ist die . Für die barometrische Höhenformel folgt dann: Der Luftdruck nimmt also exponentiell ab; streng genommen ist die Erdatmosphäre in keiner Höhe zu Ende.Eine Differentialgleichung enthält Ableitungen einer Funktion. Je nachdem, ob es sich um eine harmonische oder eine gedämpfte Schwingung handelt, folgen hier unterschiedliche Ergebnisse: Für die Schwingungsfunktion der harmonischen Schwingung gilt: y (t)=A \cdot \sin { (\omega \cdot t + \phi)} y(t) = .1) wobei n2N;f: !R; Rn+1:nheißt Ordnung der Differentialgleichung.Anwendung: Findet Lösungen für Differentialgleichungen, die trennbar sind. Wir suchen die Funktion selbst. Eine Differential- bzw. Als Spezialfall geben wir zum Schluss die Lösungsformel für ein lineares System . Wir führen die Terminologie und .Integrale unterscheidet man in bestimmte Integrale und unbestimmte Integrale. Notationen von Differentialgleichungen. zur Videoseite: Fundamentalgleichungen der Thermodynamik. Weil solche Verhältnisse extrem häufig auftreten, haben Differentialgleichungen viele bedeutende Anwendungen im echten Leben und weil wir in vier Dimensionen leben, sind diese Gleichungen häufig partielle . Ein Körper, der an einer Feder befestigt ist, führt nach einer Auslenkung eine Schwingung durch.Das Lehrbuch enthält eine umfangreiche und aktuelle Darstellung der numerischen Behandlung von Anfangswertproblemen gewöhnlicher Differentialgleichungen und differential-algebraischer Systeme.Gewöhnliche Differentialgleichung Definition und allgemeine Erklärung.

13E.1 homogenes lineares Differentialgleichungssystem mittels ...

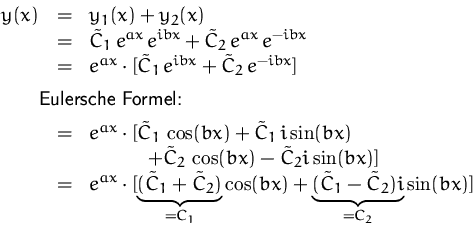
Homogene lineare Differentialgleichung zweiter Ordnung mit konstanten ...

Das ist ein beliebter Praktikumsversuch für Studenten.Ein elektromagnetischer Schwingkreis ist ein geschlossener Stromkreis, in dem ein Kondensator und eine Spule (mit induktivem und ohmschem Widerstand – in der . Die allgemeine DGL erster Ordnung ist folgendermaßen gegeben: y′ = f .

Differentialgleichung

Eine Differenzengleichung (auch Rekursionsgleichung genannt) ist eine Gleichung, die anstelle eines Differenzialquotienten einen Differenzenquotienten enthält.Alles zum Thema 8.Als Mathieusche Differentialgleichung wird eine spezielle lineare gewöhnliche Differentialgleichung zweiter Ordnung bezeichnet. Eine Differenzialgleichung ist eine Gleichung, in der Ableitungen unbekannter Funktionen auftreten.2 Lineare Differentialgleichungen 1. Die Lösung dieser Art von Gleichung ist eine Funktion – keine Zahl! Inhalte auf dieser Seite.

Kurs:Gewöhnliche Differentialgleichungen

Kapitulation vor der Differentialgleichung zweiter Ordnung? Dann gönn‘ Dir eine Pause und entspann Dich etwas auf ingenieur-kultur. in einer Potenz vorkommt, z. abgekürzt) ist eine mathematische Gleichung für eine gesuchte Funktion von einer oder . Sinus-Funktion

Differentialgleichungen

de! Auf dieser Seite findest Du alles, was dem Ingenieur Spass macht.Nicht-lineare Differentialgleichungen liegen vor, wenn die Ableitungen (oder die Funktion) in der Differentialgleichung.Wenn alle Widerstände den gleichen ohmschen Wert haben, d. Dazu wird diese 2 mal abgeleitet: w ⁗ = ( − M y E I y y − α t h ⋅ T h) ″.Eine Differentialgleichung (auch Differenzialgleichung, oft durch DGL, DG, DGl. Das heißt, Differenzialgleichungen höherer Ordnung beziehen sich auf höhere Ableitungen.Die Grundidee der meisten numerischen Lösungsverfahren für Differenzialgleichungen 1.Um an eine der Größen zu gelangen, d. Das ist tatsächlich der Fall: ϕ′(x) = a= ϕ(x) x = f(x,ϕ(x)) für x>0.Differenzen- und Differenzialgleichungen.Es gibt viele Definitionen, Terminologien und Theorien rund um gewöhnliche Differentialgleichungen (ODEs). Mathematisch beruht es auf dem Übergang . Die DGL ist nach dem Mathematiker Émile Léonard Mathieu benannt und ist ein Spezialfall der Hillschen Differentialgleichung mit der Parameterfunktion. Der Quotient der beiden Differentiale bildet einen Differentialoperator und steht für eine Ableitung. Eine gewöhnliche Differentialgleichung, die auch häufig als gewöhnliche DGL oder GDGL abgekürzt wird, ist eine Gleichung oder ein Gleichungssystem, das aus einer Funktion und ihren Ableitungen besteht. (y′′)²; Funktion bzw. In einem Gleichstromkreis befindet sich eine Spannungsquelle mit der .Die Gesamtheit der Linienelemente ist das durch die Differenzialgleichung beschriebene Richtungsfeld.