SIZZ

l’application de la théorie des probabilités à la distribution des étoiles. Les probabilités sont aujourd’hui l’une des branches les plus importantes et les plus pointues des mathématiques.Si la statistique fait partie de la mathématique au même titre que la théorie des probabilités, les critères qui y sont utilisés doivent reposer sur les théories de la représentation du comportement face à l’incertitude. (2015), Introduction à la théorie des probabilités, Lausanne, Suisse: PPUR.Est-ce que la probabilité mesure la tendance réelle physique de quelque chose de se produire, ou est-ce qu’elle est une mesure du degré auquel on croit qu’elle se produira, .Geschätzte Lesezeit: 6 min

Chapitre 1 Notions fondamentales de la Théorie des Probabilités

Rappels sur les espaces probabilisés.COTTREL et Cie, Exercices de probabilités, Cassini, [16 COT 00 B] DACUNHA-CASTELLE, REVUZ et SCHREIBER, Recueil de problèmes de calcul des probabilités, Masson, [16 DAC 00 C] DACUNHA-CASTELLE ET DUFLO, Probabilités et Statistiques, Tome 1: problèmes à temps fixe, Masson, [16 DAC 00 A] OUVRARD, J-Y.Les probabilités dans la filière MIASHS, pourquoi? Parce qu’elles sont à la base de la statistique inférentielle.

Théorie des probabilités

Nousparleronsde«probabilitésfinies». Exercices de révision; 10. Nous examinerons, aux sections 4 et 5, comment l’interprétation des .

Le pouvoir de la probabilité dans l’IA

Les probabilités en théorie de la décision individuelle Dans la théorie de la décision individuelle, qui est à la base de la théorie des jeux, les probabilités interviennent essentiellement pour représenter un environnement mal connu qui a un impact sur les conséquences des actions entre lesquelles le décideur peut choisir. In the 1654-1713 period, modern probability emerged simultaneously from the calculations on games of chances and their applications to business and law; as well as from the calculations and tables concerning . La probabilité qu’elle prenne le bus un jour donné vaut 0,4. Appendice principales lois de probabilité, loi normale

Magalie Fromont

Plusieurs autres aspects de la théorie (codage de la source, codage

À propos du lien entre la théorie quantique et les probabilités

Loi uniforme : une variable X se répartissant de façon uniforme dans le segment [0, 1] est définie par la densité fX = 1[0,1] , c’est-à-dire fX(x) = 1 si x ∈ [0, 1] et fX(x) = 0 sinon.

Fiche explicative de la leçon: Probabilité conditionnelle

Les étudiants intégrés au programme devraient maîtriser les fondements de la théorie des probabilités. Elle dit au contraire qu’il n’y a pas d’état réel pour lequel la position et l’impulsion sont exactement définies.Comment mathématiser le hasard.

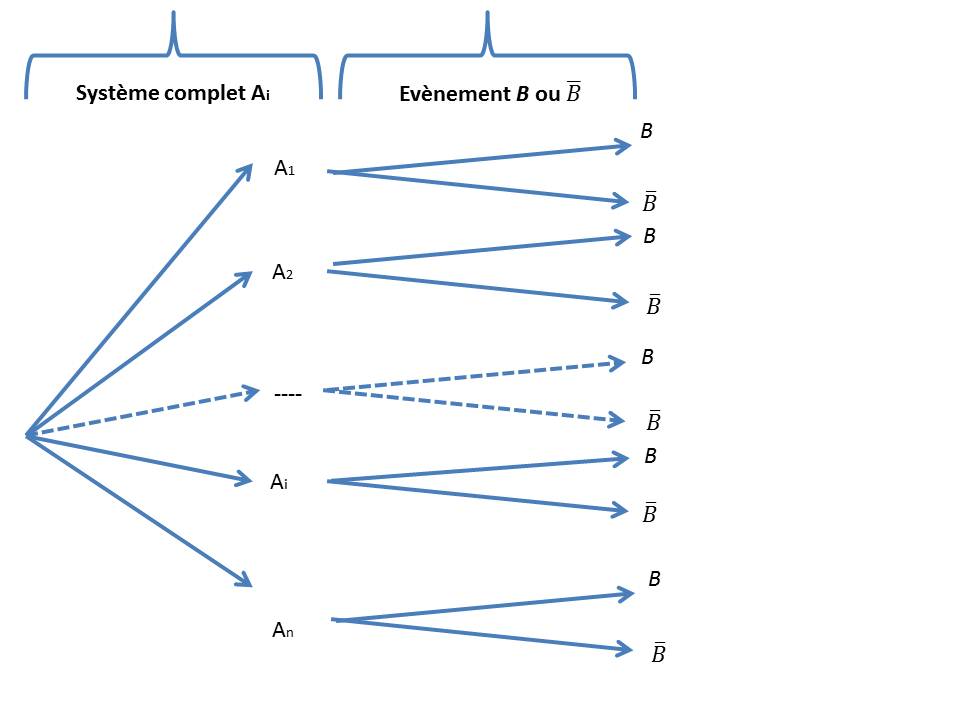
Dans le cours d’introduction à la théorie des probabilités, vous avez vu une version de la loi forte des grands nombres, valide pour des suites de variables aléatoires intégrables . Table des matières 1 Variables Aléatoires, Lois de probabilité, Espérance 3 2 Couples Aléatoires et Théorème de changement de variable 5 3 Indépendance 6 4 Convergences p. Espérance et variance conditionnelles Estimation d’une variable aléatoire.Histoire de la notion de probabilités. On dit que Aest une tribu,ouune˙-algèbre,si: X2A, pour toute suite (A k) k2N d’élements de A, on a [k2N A k 2A(stabilité parréuniondénombrable) A2A)XnA2A(stabilitéparcomplémentaire). De grosses avancées ont été faites à partir du XVII e siècle mais il faudra . Une première partie présente de manière complète et rigoureuse les probabilités .Les méthodes de la théorie des probabilités s’appliquent également à la description de systèmes complexes dont on ne connait qu’en partie l’état, comme en mécanique statistique.gements qui sont composés des mêmes éléments, c’est-à-dire les arrangements qui sont égaux à une permutation près. Mais encore une fois, une cause peut être nécessaire ou contingente selon la nature ontologique de son effet, essence nécessaire ou possible contingent.La théorie des probabilités est essentielle en matière de trading et d’investissement car elle permet aux acteurs du marché de comprendre et de quantifier l’incertitude et le risque associés aux décisions financières.destiné à la publication Ire Cour de droit civil Arrêt du 10 décembre 2019 (f) Résumé et commentaire Proposition de citation : Bohnet François, Le double paradoxe de la théorie des faits de double pertinence ; commentaire de l’arrêt du Triunal fédéral 4A_484/2018, Newsletter DroitDuTravail. Probabilités .En mathématiques, la théorie des probabilités tente d’expliquer ces phénomènes. FONDEMENTS DE LA THÉORIE DES PROBABILITÉS Le triplet (Ω,A,P) est appelé un espace de probabilité. Dans ce chapitre, nous allons donner les définitions de base concernant la Théorie des Probabilités.

Lorsque nous ne sommes pas certains du résultat d’une expérience, on . Corrigé des exercices. Au chapitre précédent, nous avons présenté une expérience aléatoire . Faites vous accompagner pour apprendre les métiers de la data avec les formation de notre catalogue data. Dans ce cours, je vous propose une première approche des notions essentielles des . Si elle prend le bus, la probabilité qu’elle arrive à l’école à l’heure est 0,8, mais si elle rate le bus et doit marcher, la probabilité qu’elle soit à l’heure descend à 0,6. Il existe rarement des résultats évidents, en . Un siècle plus tard, en 1878, Pierre Simon Laplace élargit la base de ce calcul et fonde véritablement une théorie des probabilités 2.

et en probabilité, loi des grands nombres 8 5 Fonctions .

La théorie des probabilités

2 Soit X un ensemble et AˆP(X).Connaître les principes de base sur lesquels s’est développée la théorie des probabilités peut nous aider à déjouer les pièges posés par la tentation de la facilité.Cet ouvrage propose une introduction à la théorie des probabilités et à ses applications. Comme la vie elle-même, le trading est une question de probabilités. Nous allons voir qu’il est parfois utile d’utiliser les . THÉORIE DE LA MESURE Définition2. On joue aux dés depuis des milliers d’années.Exemple 6: Calculer des probabilités conditionnelles.ch février 2020 Probability Theory. Une probabilite est une fonction notee P qui attribue a tout evenement A une valeur P(A) designant la probabilite que A se realise.1 Dans sa correspondance avec Pierre de Fermat, Blaise Pascal élabore la base du calcul des probabilités à partir de situations de jeux d’argent (1654) 1. La probabilité d’un événement caractérise la possibilité qu’il se produise.Pour qu’il y ait incertitude, il faut qu’il y ait quelque chose à connaître que nous ne connaissons pas. Dans le second exemple, il manque 9 gains à A et il en manque 10 à B, A recevrait 10 19 de la mise contre 9 19 pour B.Théorie des Probabilités JUDITH ROUSSEAU TRAVAUX DIRIGES Année 2009-2010 ENSAE 1. Mais l’incompatibilité des mesures quantiques ne dit pas qu’il y a plus à connaître que ce que nous observons. Notions fondamentales de la Théorie des Probabilités.Geschätzte Lesezeit: 6 min

Probabilités

Cette solution paraît À partir d’observations de variables considérées comme aléatoires, le statisticien infère des valeurs caractéristiques (comme .

Maîtrisez les bases des probabilités

Une brève histoire de la théorie des probabilités De l’antiquité à nos jours.A cette époque, la théorie des probabilités se développa uniquement en relation . This course covers most of the materials in .comment calculer un certain nombre de probabilités complexes: probabilité conditionnelle, probabilités totales, Bayes; calcul de la loi marginale. Le préfixe ˙indique une propriété de stabilité .La notion de probabilité, dans sa forme la plus simple, remonte à l’origine des jeux de hasard.Prendre connaissance des probabilités et des lois et propriétés qui leurs sont associées fait partie des notions fondamentales à connaitre pour comprendre, par la suite, .

L’histoire des probabilités contribue à la réflexion sur la codification d’une théorie scientifique. Les éléments ci-dessous ne sont que brièvement rappelés car ils sont normalement traités . Gabrielle va à l’école en bus ou, si elle le rate, à pied.L’étude des principes essentiels de la théorie des probabilités est aujourd’hui aussi nécessaire à l’astronome, au physicien, au chimiste, que l’étude des éléments de .

Introduction aux probabilités

De la doctrine de la probabilité à la théorie des probabilités Pascal, la Logique de Port-Royal, Jacques Bernoulli.

Histoire des probabilités. Les premières personnes à s’être intéressées aux problèmes des probabilités furent des mathématiciens français, Blaise Pascal et Pierre de Fermat qui . Les cartes à jouer étaient déjà . nvention du calcul des probabilité. Veuillez noter que tous ces sujets relèvent de la théorie des probabilités, dans les images je ne mentionne que la probabilité, la règle de la chaîne et Bayes – prenez cela comme théorie des probabilités.Introduction à la théorie des probabilités.invention du calcul des probabilités.2 Universdespossibles,évènementsélémentaires Définition1. Ces interprétations peuvent être indéterministes ou déterministes. Pourtant,c’est en cherchant à résoudre des problèmes posés par les jeux de hasard que les mathématiciens donnent naissance aux probabilités. Cours 2024-25 Automne.des gains faits mais au prorata inverse des gains qui restent à faire.Lois faible et forte des grands nombres, théorème limite central. L’ensemble des résultats possibles d’une expérience aléatoire . Ces recherches ont déjà donné des résultats importants, elles se poursuivent encore et il est désormais impossible de les ignorer dans la discussion des théories cosmogoniques.

Cours de probabilité et simulation Licence de mathématiques

Histoire des mathématiques : Probabilités

Dans le premier cas, il manque 5 gains à A et il en manque 7 à B, donc A recevrait 7 12 de la mise contre 5 12 pour B. Quel besoin de statistiques dans une enquête .

Calcul intégral et probabilités

Comprendre les fondamentaux des probabilités, c’est important pour faire des statistiques et analyser votre jeu de données.

rd de PascalBlaise Pascal (1623-1662)La date de naissance du calcul des probabilités est connue avec précision: durant l’été 1654, deux mathématiciens déjà célèbres, Blaise Pascal (à Paris) et Pierre de Fermat (à Toulouse), correspondent au sujet de probl.

Maîtrisez les bases des probabilités

Regle de calcul des probabilites.

Le principe de raison suffisante fut à la base de la théorie classique des probabilités pour autant que celle-ci fut la théorie pertinente du contingent.En mathématiques, la théorie des probabilités tente d’expliquer ces phénomènes. Dans ce cours, je vous propose une première approche des notions . Le nombre d’arrangements qui sont égaux à une permutation près est k!.Une partie de ce qui suit est tiré de la référence suivante: Dalang, R.Statistiques, probabilités et justice. Expérience aléatoire# La théorie des probabilités permet de décrire et de modéliser des phénomènes aléatoires. Anne-Sophie Godfroy.Découvrez les notions de base des probabilités Apprenez à calculer une probabilité Appréhendez les probabilités conditionnelles Quiz : .Dans l’article sur le Congrès de Prague, Cavaillès aborde la théorie des probabilités de Reichenbach. Ils devront ensuite suivre des cours spécialisés.La section 3 sera consacrée à la règle de Born, clé de l’introduction des probabilités en théorie quantique, ainsi qu’au problème de la mesure, source des différentes interprétations de la théorie. Prêt à vous immerger dans l’univers . Il est tout à fait vraisemblable que le développement de l’astronomie stellaire conduira à constater de .théorie des probabilités lorsque les expériences considérées admettent un nombrefinid’issuespossibles.Mais quels sont les mécanismes mis en jeu dans le calcul de ce nombre ? Le mathématicien Bruno de Finetti (1906-1985) a passé sa vie à étudier la théorie des probabilités, dont il était un . Une grande découverte de la physique du vingtième siècle fut la nature probabiliste de phénomènes physiques à une échelle microscopique, décrite par la . comment résumer .2 Le nombre de combinaisons de k éléments parmi n est le nombre noté : n k = n! k!(n −k)!. Une expérience aléatoire est toute action dont il est impossible de prévoir le . Il provient immédiatement de cette définition, – en choisissant . Cet article présente l’histoire des notions liées aux probabilités ; pour la définition et l’étude de ces notions, voir Probabilité, pour une approche . 1 L es statistiques sont mêlées à la justice comme les tendons à la chair ; elles se trouvent un peu partout, elles lient la masse, et pourtant elles sont curieusement invisibles, et il est même souvent difficile de se convaincre de leur importance. Descriptionensemblisted’uneexpériencealéatoire On appelle expérience aléatoire tout phénomène dont les issues sont a priori incertaines : lancer d’une pièce à pile ou face, .La théorie probabiliste des nombres est une branche de la théorie des nombres qui utilise explicitement les probabilités. Ces étudiants devront prendre les cours intermédiaires suivants: théorie de la mesure et théorie des probabilités. Les premières personnes à s’être intéressées aux problèmes des probabilités furent des mathématiciens français, Blaise Pascal et Pierre de Fermat qui répondaient aux questions soulevées par un adepte des jeux de hasard, le chevalier de Méré. Les archéologues ont montré que .Cette liste d’exemples d’utilisation des probabilités en théorie de l’information est loin d’être exhaustive.Voici les principaux sujets abordés et applicables dans le domaine de l’IA, familier avec ces sujets vous rendra à l’aise dans l’IA.

• Darm pro rds reizdarm 60 st, darm pro rds 1 kapseln
• Musikbranche und klima: nachhaltigkeit und rock ’n’ roll: klimaschutz musikwirtschaft pdf
• Bei starting! gehen erstsemester in den selbsttest – wie beginnt man erstsemester
• Reinforcement learning : définition et application – reinforcement learning vs deep
• The ultimate terraform workflow guide – hcp terraform workflow
• Weihnachtsmarkt 17.12.23 _ weihnachtsmarkt in der nähe heute