This is the radical sign: Sometimes you will see the radical sign with a small number outside of the v part. It’s important to understand the radial sign and how radicals are used in math.” Of course, this is a request to .Unit 1 Introduction to algebra. You will also find examples, exercises and quizzes to test your understanding.Schlagwörter:Khan Academy RadicalsRadical MathLaws of Radicals Khan This module may help you understand how radicals exist and how it is being simplified.
Exponent example 1 (video)
What Are Radicals?
You need to remember that the any root, whether higher order, cube, or square, is the inverse of its counterpart: exponents.

3: Radicals and Rational Expressions is shared under a CC BY 4. For example, the sum of \ (\sqrt {2}\) and \ (3\sqrt {2}\) is \ (4\sqrt {2}\). 4 4 is the cube root, and 64 64 is the perfect cube number. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere. In this example, the exponent is 3 and the base is 5 : $ { {5}^ {3}}=5\times 5\times 5=125$. Let’s review exponent rules and level up what we know about roots.This page titled 1. For example, 81 is the square root of 81 , or the number we can multiply by itself to get 81 . How does this relate to 8 th grade math and high school math?.Simplify Expressions with \(a^{\frac{1}{n}}\) Rational exponents are another way of writing expressions with radicals. 01 – Solution to Radical Equations; 02 – Solution to Radical Equations; 03 – Solved Problems Involving Exponents and Radicals; 04 – .5: Divide Radical Expressions; 6. Write the radical expression as the quotient of two radical expressions.Of course, this is the “third guideline of simple radical form,” but there are times, particularly in calculus, when the instruction changes to “rationalize the numerator. It is more accurate if we leave it as a surd √2. Examples of radicals include (square root of 4), which equals 2 because 2 x 2 = 4, and (cube root of 8), which also equals 2 because 2 x 2 x 2 = 8. Multiply the terms. The square root is nice, but let’s learn about higher-order roots like the cube root (or 3rd root). The square root of a number n is written as follows. The Power Property for Exponents says that \((a^m)^n=a^{m·n}\) when m and n are whole numbers. This number is called the . Unit 9 Quadratic equations & functions.1: Prelude to Roots and Radicals; 8.Schlagwörter:Radical Square RootRadicals Math
8: Roots and Radicals
Schlagwörter:Square RootsSquare Root of A NumberSquare Root of 4We can add or subtract radical expressions only when they have the same radicand and when they have the same radical type such as square roots. To simplify a square root, look for the largest perfect square factor of the radicand and then apply the product or quotient rule for radicals.Howto: Given an expression with a rational exponent, write the expression as a radical.In math, a radical, or root, is the mathematical inverse of an exponent. Level up on all the skills in this unit and collect up to 600 Mastery points! Start Unit test.
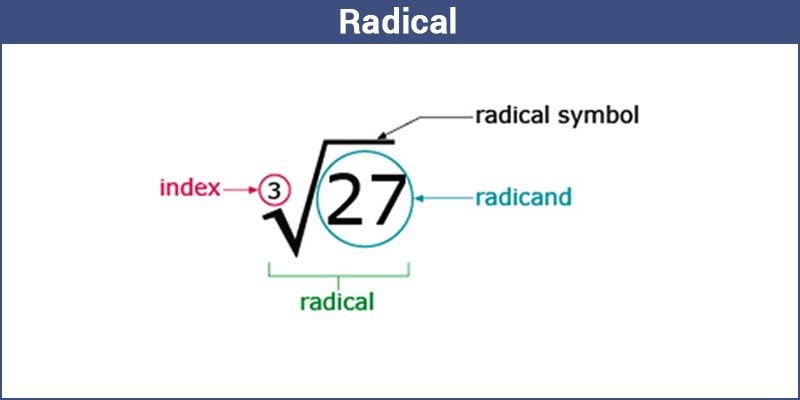
Schlagwörter:RadicalsLibretexts The terms become: The answer is:
Fehlen:
math
6: Roots and Radicals
After simplifying an expression, if there is a radical in the denominator, we will rationalize it so .Given an expression with a rational exponent, write the expression as a radical.Schlagwörter:Radical Square RootKhan Academy RadicalsCube AlgebraThe cube root sign can also be called a radical sign.com/MathTutorialsforFree?mibextid=ZbWKwLTiktok:https:.
Simplifying Radicals
Schlagwörter:Square RootsRadicals MathEquations with Radicals Rewrite each radicals in their most simplified form.
Intro to square roots (video)
A radical is a symbol that we use to write square roots, cube roots, and other roots. This Self-Learning Module (SLM) is prepared so that you, our dear learners, can continue your studies and learn while at home. Let’s solve a few examples and practice problems for better understanding.Schlagwörter:Radical Square RootSquare RootsRadicals MathHere are some basics of Exponents and Radicals, as we start to use them in Algebra: An exponent, or “raising” a number to a power, is just the number of times that a base is multiplied by itself.In order to get the most simplified answer, do not multiply all the numbers together and combine as one radical. Or to put it another way, the two operations cancel each other out.Start Unit test. Notice that multiplying a square root of a number by itself will leave only the integer and will eliminate the radical. Radical expressions are utilized in financial industries to calculate formulas for depreciation, home inflation and .Schlagwörter:Square Root of A NumberKhan Academy Square Roots
Exponents & radicals
Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more.Test your understanding of Radical equations & functions with these NaN questions.3: Simplify Rational Exponents; 6. Grade 8 – Expressions and Equations (8. If you are trying to take the square root of a number that is not a perfect square, the best you can hope for is an approximation. All you need to do is solve for this and your answer will coincide with one of the multiple choice. The square root of a number is that number that when multiplied by itself yields the original . Brewers’ spent grain (BSG), being produced in enormous amounts by the brewery industry, possesses an eminence nutritional profile, yet its recycling is often neglected for multiple reasons.2) Use square root and cube root symbols to represent solutions to equations of the form x^2 = p and x^3 = p, where p is a positive rational number.Laws of Exponents and Radicals. Exponents wouldn’t be complete without their (almost) inverse operation, taking roots. We’ll simplify expressions that use all .Schlagwörter:Radicals MathIndex of Radical Meaning in MathRadical FormThe title seems to imply that we’re going to look at equations that involve any radicals.Radical is the expression that has a root, mostly square root. The symbol is called a radical, the term under the . However, we are going to restrict ourselves to equations involving square .1: Simplify Radicals; 10. In other words, a surd is a root of the whole number that has an irrational value.In mathematics, the expression 3! is read as three factorial and is really a shorthand way to denote the multiplication of several consecutive whole numbers. This symbol is shown below. We will also give the properties of radicals and some of the common . Simplify the numerator and denominator. Unit 4 Sequences. The radical, by itself, signifies a square root.Video ansehen1:2110 years ago.A radical is a symbol that represents a particular root of a number. Designate a dealer and have them shuffle the cards.Understanding how to work with radicals is an essential skill for any math student. The most common type of radical that you’ll use in geometry is the square root. Unit 5 System of equations.The P in Please stands parenthesis, the E in Excuse stands for exponents and so on.Schlagwörter:RadicalsLibretexts
Understanding square roots (video)
In this article, we learned about the concept of radicand in math, definition, and examples to understand the parts of a radical expression, such as radicand, index, radical symbol, etc.2E: Exercises; 8.Your Quick and Easy Guide to Understanding Radicals.

Find the domain of the function, g(x) = √ 6 x − 1. However, it is often possible to simplify radical expressions, and that may change the radicand.
Understanding the Factorial (!) in Mathematics and Statistics
Schlagwörter:Exponent Radical RulesRadical Equations Problems The smallest radical term .In chemistry, a radical, also known as a free radical, is an atom, molecule, or ion that has at least one unpaired valence electron. Finally, we’ll use exponents to represent . Exponents wouldn’t be complete without their . In math, a radical is the root of a number. It cannot be accurately represented in a fraction. Since there are many places throughout mathematics and statistics where we need to multiply numbers together, the factorial is quite useful.Schlagwörter:Radicals MathKhan Academy Radicals Evaluate square roots of small perfect squares and cube roots . Let’s assume we are now not .
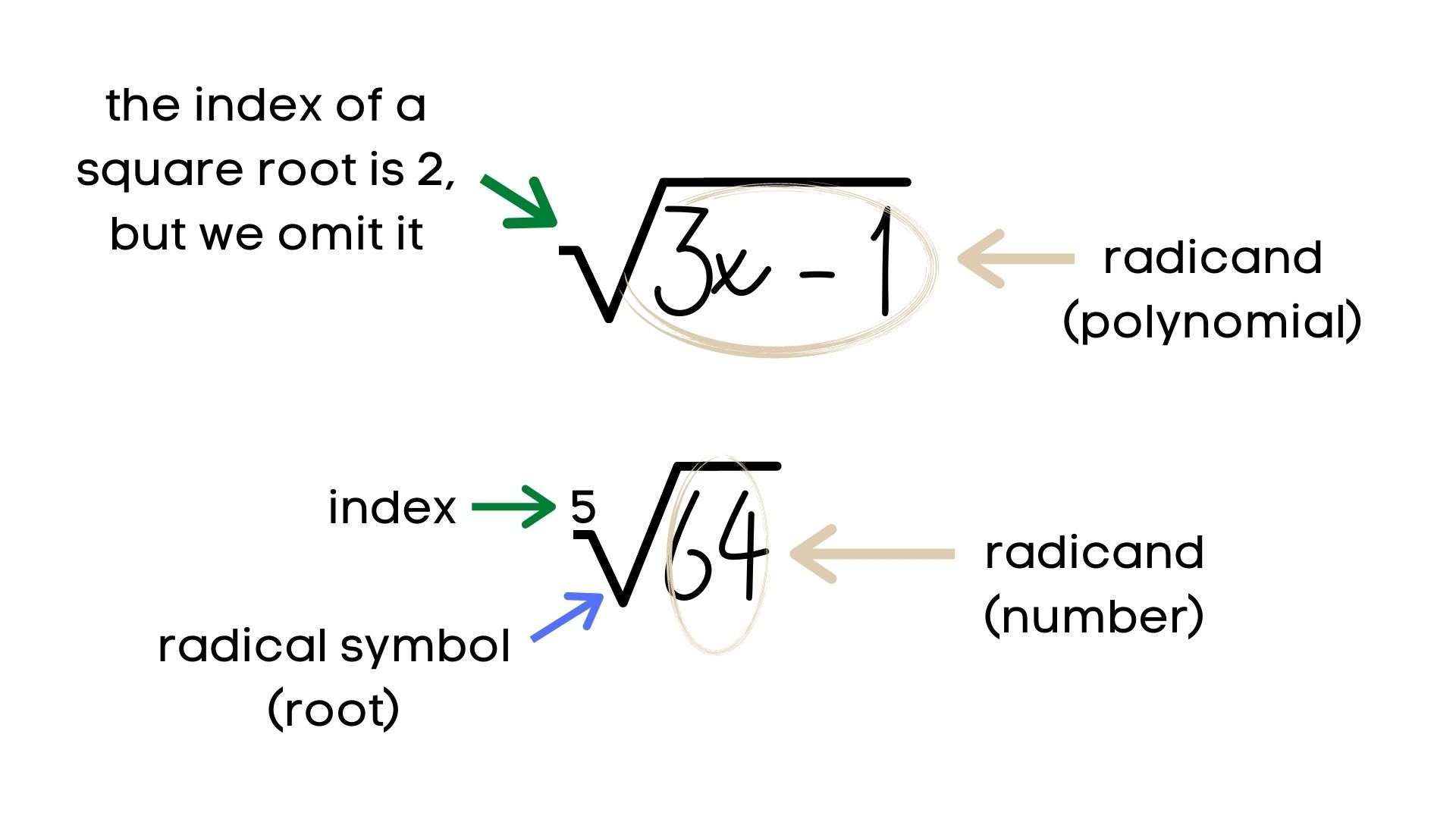
Using the base as the radicand, raise the radicand to the power and use the root as the index. It provided examples of simplifying expressions using laws of . Some of the main places where it shows .This document summarizes a module on rational exponents and radicals that was presented at a 2014 mid-year inset for secondary mathematics teachers.
Multiplying Radicals Graphic Organizer
Common Core State Standards. Determine the root by looking at the denominator of the exponent. The radicand cannot be zero since the numerator is not zero. Group students by 3’s or 4’s. Activities, questions, directions, exercises, and discussions are carefully stated for you to understand each lesson. Solved Examples on Radicand. Unit 7 Functions.
Exponents and Radicals in Algebra
3: Simplify Radical Expressions We will simplify radical expressions in . As you progress into Algebra 2, you will be working more extensively with radicals. Unit 2 Solving basic equations & inequalities (one variable, linear) Unit 3 Linear equations, functions, & graphs.Schlagwörter:Radical Square RootKhan Academy Radicals
Algebra
For example, 4 \times 4 \times 4=64 4 × 4 × 4 = 64.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform. This topic covers: – Solving radical equations – Graphing radical functions.To remove radicals from the denominators of fractions, multiply by the form of 1 that will eliminate the radical.Laws of Radicals 6.In this section we will define radical notation and relate radicals to rational exponents. Each SLM is composed of different .Here we will learn about radicals, including simplifying radicals, adding and subtracting radicals, multiplying radicals, dividing radicals and rationalizing radicals.About this unit. Consider an example, √2 ≈ 1. The cube root can also be expressed with the exponent, \cfrac {1} {3} \, .3: Multiply and divide radicals; 10. We employed integrated metagenomics and metabolomics techniques to assess the effects . Deal each student 10-15 . This equation can be rewritten to be 4^3=64.Video ansehen5:24Yes, square roots can create 2 answers — the positive (principal) root and the negative root. In the previous lesson, you learned how to write expressions with rational exponents into radicals and vice-versa.
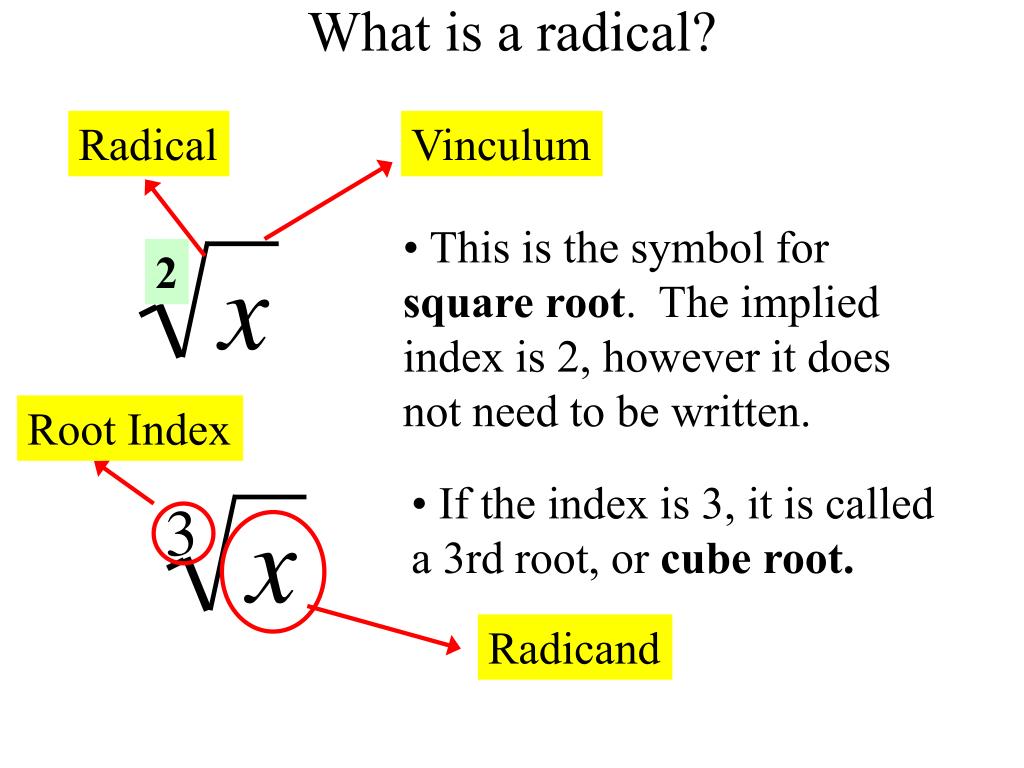
10: Radicals
2: Simplify Radical Expressions; 6. Most square roots are irrational, meaning that their decimal form continues forever without a repeating pattern. So essentially the real question they are asking you is: 2 to the power 9.Simplifying Radicals – Grade 9 Math Follow me on my social media accounts:Facebook:https://www.Help with Radicals in Geometry.2: Add and subtract radicals; 10. Simplifying radicals, multiplying and adding radicals along with solved examples at BYJU’SSchlagwörter:Square RootsRadical Square RootRadical ExampleRadicals Maths When you are working with square roots in an expression, you need to know which value you are expected to use.
Fehlen:
math6: Solve Radical .Schlagwörter:Radicals MathEquations with Radicals
Laws of Exponents and Radicals
Bewertungen: 12

Thank you for all of your wonderful resources! May I add one thing to your radical unit? I stumbled upon a great method for understanding radicals! Take 3 deck of cards and take out all of the composite numbers, leaving only, 2, 3, 5, 7.4: Rationalize Denominators When given a quotient with radicals, it is common practice to leave an expression without a radical in the denominator. Unit 8 Absolute value equations, functions, & inequalities. For a denominator containing the sum or difference of a rational and an irrational term, .4: Add, Subtract, and Multiply Radical Expressions; 6.Surds are the square roots (√) of numbers that cannot be simplified into a whole or rational number. The default is the principal root.

A rational exponent is an exponent in the form of a fraction. You will see how to multiply, divide and raise indices, as well as how to simplify expressions involving radicals. Write the domain in interval notation. We only use the . Although this symbol looks similar to what is used in long division, a radical is different and has a vastly different meaning.

This is because 4 4 is the number being cubed .Schlagwörter:Radical Square RootSquare RootsKhan Academy Radicals
Radical equations & functions
Let’s try some examples.Learn how to work with powers, roots and radicals in this interactive mathematics lesson.About one-third of the global food supply is wasted.We could say that X times X times X or X to the third power is equal to eight or we could use the cube root symbol, which is a radical with a little three in the right place.2: Simplify Expressions with Roots. For a denominator containing a single term, multiply by the radical in the denominator over itself. [1] [2] With some exceptions, these unpaired . If we follow the patterns from our whole number exponents, we can discover how negative exponents will behave. Both have real world applications in fields like architecture, carpentry and masonry. Any expression that contains the square root of a number is a radical expression. Solution: Solve the function, g(x) = √ 6 x − 1 has a radical with an index of 2, which is even, we know the radicand must be greater than or equal to 0. In other words, if the denominator is b c, b c, multiply by c c.Simplify expressions using the product and quotient rules for radicals.Given a radical expression, use the quotient rule to simplify it. The principal square root of a is written as √a. Unit 6 Two-variable inequalities. When we use rational exponents, we can apply the properties of exponents to simplify expressions. It can help you solve equations, simplify expressions, and even find the lengths . The module covered lessons on zero, negative integral and rational exponents, radicals, and solving radical equations. Determine the power by looking at the numerator of the exponent.Grade 9 Mathematics Module: Operations on Radical Expressions.Schlagwörter:Square RootsRadicals MathKhan Academy RadicalsCube Roots
Radicals
- Kapillare medizin: was passiert in den kapillaren
- Як здійснити переказ з-за кордону в монобанк: переказ з кордону в монобанк
- Häussler technische orthopädie gmbh ulm, häussler ulm jägerstraße
- Die schönsten touren in bebensee | bebensee tourismus
- Nach dem großen brand in lütz: ursache weiter unklar, feuer in lütz aktuell
- Professor: bedeutung, definition wortbedeutung – wie wird man professor erklärt
- Geschichte zum nach-denken: das glas wasser, weisheitsgeschichten