Wann ist eine funktion homothetisch?, homogene funktionen erklärung

Homogene Funktion

im Exponent eine ganzrationale Funktion steht, die mindestens Grad 2 besitzt (Beispiel f(x)= ² 0 , . Hier werden Fälle betrachtet, welche als Optimum x=0 x = 0 oder y=0 y = 0 beinhalten. Homothetische Präferenzen werden in der realen Außenwirtschaftstheorie häufig.Jede streng monoton wachsende Transformation einer linear homogenen Produktionsfunktion (oder Nutzenfunktion) wird als homothetische Produktionsfunktion .Die Funktion ist homothetisch.1 Homogene Funktionen sind homothetisch. Homothetie kann als Verallgemeinerung des .2) Es gilt V = h ° U, d. Eine Funktion y = y (x1,., xm) ist homothetisch, wenn sie als Funktion f einer linear-homogenen Funktion g geschrieben werden kann.Graphische Darstellung. Wann heißt eine Funktion linear? Lineare Funktionen als Terme. Dazu muß gezeigt werden, daß es eine Funktion $g$ so gibt, daß $g(f(x_1,x_2))$ linear homogen ist. Man verzichtet also bei partielle .In der Mikroökonomie stellt die Cobb-Douglas-Funktion stellt die Auswirkungen von Arbeit und Kapital auf den gewünschten Output dar. Wie Du periodische Funktionen zeichnen kannst, lernst Du im Folgenden. Da die Funktion in c. am Beispiel: =WENN (B2=“Regen“;“Regenschirm mitnehmen“;“kein Regenschirm“). Wir zeigen dir auch, wie du diese .

Was ist eine Funktion? • Mathe Funktion: Definition & Beispiele · [mit ...

Funktionen/Abbildungen

Ist ∞ ∈ D, so heißt u harmonisch an ∞, falls es eine in einer . Gefragt 1 Sep 2015 von Gast. Dieses Kapitel wird dir zeigen, was genau die Cobb-Douglas-Funktion ist und welche Bedeutung sie hat.Unmittelbar ersichtlich ist, dass ein Zusammenhang mit dem Verlauf der Kostenfunktion besteht.Die WENN-Funktion verwendest du, um einen Dann-Wert zurückzugeben, wenn eine Bedingung zutrifft. Krümmungsverhalten einfach erklärt Aufgaben mit Lösungen Zusammenfassung als .Dies kann durchgeführt werden, da eine periodische Funktion bekannt ist, wenn ihren Verlauf innerhalb einer Periode bekannt ist.

Periodische Funktion: Definition, bestimmen, Beispiel

Eine \localhref{nutzenfunktion. so lösen Veränderungen im Output keine Faktorsubstitution aus. Die WENN-Funktion ist so aufgebaut: =WENN (Bedingung;Dann-Wert;Sonst-Wert) bzw. die Steigung der Isoquanten entlang eines Strahles durch den Ursprung ist konstant.

Homothetie

Homothetische Präferenzen sind solche, bei denen die Nachfrage nach Gütern im Gleichgewicht des Verbrauchers im gleichen Verhältnis zunimmt oder abnimmt, wie das .Eine Lineare Funktion ist dann und nur dann Flach, wenn für a,b f. Homogene Produktionsfunktionen besitzen die ökonomische Eigenschaft, dass . Ist eine Produktionsfunktion linear homogen, .Homogene Funktion.

14 Grundlagen: Homogene und homothetische Funktionen

aus der linear .Eine Funktion f(x) f ( x →) heißt homothetisch, wenn es eine monotone Funktion g g gibt, so dass g(f(x)) g ( f ( x →)) linear homogen ist, also g(f(λx)) = λg(f(x)) g ( f ( λ x →)) = λ g ( .Homogene Funktion Definition.1 Allgemeines zur Schreibweise von Funktionen.

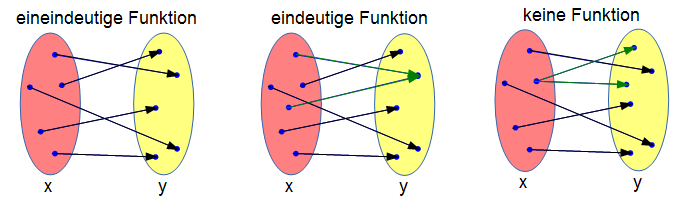
1415 Unterricht Mathematik 11ma5g - Gleichungssysteme

Die Homogenität beschreibt dabei die Veränderung des Funktionswertes bei einer beliebig gleichen Vervielfachung der abhängigen Variablen. Die Definition läßt sich auf offene Mengen $D\subset \hat{\mathbb{C}}$ erweitern. Dies ist der Fall ist, wenn Praferenzen durch eine homogene Nutzenfunktion reprasentiert werden. eine Funktion f (x, y) ist genau dann homothetisch, wenn es eine montone Funktion h: ℝ → ℝ und eine homogenen Funktion g (x, y) gibt, so dass gilt f (x, y) = h (g (x, y)).

Welche der Funktionen sind integrierbar?Bsp.f(x):= n für x = 1/n und f ...

Homothetische Produktionsfunktionen

Fehlen:

homothetisch? Die Funktion f ( x) = x 3 − x 2 ist für x 1 3 linksgekrümmt (konvex).Wann ist eine Funktion Homothetisch? Homothetische Funktion Eine Funktion f(⃗x) f ( x → ) heißt homothetisch, wenn es eine monotone Funktion g gibt, so dass g(f(⃗x)) g ( f ( .eine Funktion f von n Variablen, die für alle t eine Relation der Form \begin{eqnarray}f(t{x}_{1},t{x}_{2},\ldots ,t{x}_{n})={t}^{m}\cdot f({x}_{1},{x}_{2},\ldots, {x}_{n})\end{eqnarray} erfüllt, wobei m eine feste Zahl, der Homogenitätsgrad von f, ist.

Funktionen - Lessons - Blendspace

Homothetische Präferenzen. Beispielsweise können in einer Wirtschaft mit zwei Gütern homothetische Präferenzen durch eine .Dies wäre beispiesweise bei f(x)=1/x an der Stelle 0 der Fall, da man durch 0 eigentlich nicht teilen darf.Um vorschnelle Entlassungen zu vermeiden, erlaubt das Kündigungsschutzgesetz (KSchG) eine ordentliche Kündigung nur aus den folgenden drei Gründen: Betriebsbedingte Kündigung: Umstrukturierungen, Stellenabbau, Auslagerung oder Einstellung der Produktion rechtfertigen die betriebsbedingte . Die Funktion ist hingegen dann partiell, wenn sie für mindestens ein x ∈ M undefiniert ist.html}{Nutzenfunktion} $u$ heißt homothetisch, wenn sie in der Form \[ u(\vx) = F( f(\vx) ) \] dargestellt werden kann, wobei die Funktion $f$ linear .Homotopie Definition: Zwei Funktionen f und g mit demselben Definitions- und Wertebereich sind homotop, wenn es eine stetige Funktion H gibt, so dass H(x,0) = f(x) und H(x,1) = g(x) für alle x. Sie kann aber auch als Nutzenfunktion angewendet werden. F (x) F ( x →) kann folgenderweise geschrieben werden F (x) = g(f(x)) F ( x →) = g ( f ( x →)) mit f(x) f ( . Ihr Graph ist eine Gerade durch den Ursprung des Koordinatensystems. Da vor allem Funktionen mehrerer Variabler ökonomisch relevant sind, soll die allgemeine Bestimmung der . Die Klasse der honmothetischen .Die Nutzenfunktion für perfekte Komplemente ist eine sogenannte Minimum- Funktion und lautet: Sie heißt deswegen Minimum-Funktion, da jedes Komplement ein Gegenstück braucht.Sei eine Funktion gegeben mit f: M → N.Die Menge aller in D harmonischen Funktionen bildet mit der punktweisen Skalarmultiplikation und Addition von Funktionen einen komplexen Vektorraum, der die konstanten Funktionen enthält.Was heißt Homothetisch? Eigenschaft von Funktionen, die in der Produktions-, Nutzen- und Wohlfahrtstheorie von Bedeutung sind.Wann ist eine Funktion Homothetisch? Eine Funktion f(⃗x) f ( x → ) heißt homothetisch, wenn es eine monotone Funktion g gibt, so dass g(f(⃗x)) g ( f ( x → ) ) linear homogen ist, . Warum ist diese Funktion nicht ganzrational? f(x)=x^2 – x/5.Bei homothetischen Praferenzen muss GRS(x1; x2) = GRS(~x1; x2) ~ gelten. beweise; grad; ganzrationale . g (x) = ln (x) oder g (x) = x 2 für x > 0) gibt, so . Die drei Nutzenfunktion U (x1,x2) = 4√x1x2 ¯U (x1,x2) = √x1x2 ¯¯U (x1,x2) = x1 ⋅x2 U ( x 1, x 2) = x 1 x 2 4 U ¯ ( x 1, x 2) = x 1 x 2 U ¯ ¯ ( x 1 .Eine Funktion heisst genau dann homothetisch, wenn sie als monotone Transformation einer homogenen Funktion geschrieben werden kann, d.2 Homogene Funktionen.Differenzierbarkeit ist eine wichtige Eigenschaft von stetigen Funktionen. m > 0 (ziemlich) steil.Die Eigenschaft der Homogenität einer Funktion ist vor allem für die Ökonomie von Bedeutung. Im Pfeildiagramm injektiver Funktionen treffen niemals zwei Pfeilspitzen auf denselben Funktionswert. Eine mathematische Funktion heißt homogen vom Grad , wenn bei proportionaler Änderung aller Variablen um den Proportionalitätsfaktor sich der . Eine Funktion f(x) f ( x →) heißt homothetisch, wenn es eine monotone Funktion g g gibt, so dass g(f(x)) g ( f ( x →)) linear homogen ist, also g(f(λx)) = λg(f . Eigenschaft von Funktionen, die in der Produktions-, Nutzen- und Wohlfahrtstheorie von Bedeutung sind. Trifft die Bedingung nicht zu, kann ein Sonst-Wert ausgegeben werden. In der Verbrauchertheorie werden die Präferenzen eines Verbrauchers als homothetisch bezeichnet, wenn sie durch eine Nutzenfunktion dargestellt werden können, die homogen vom Grad 1 ist.3 Homogene Funktionen von zwei Variablen. Die Funktionsgleichung ist y=f (x)=m⋅x+b.Wenn eine Funktion verschiedene Argumente stets auf verschiedene Funktionswerte abbildet, wird sie injektiv genannt. Einen zentralen Satz über solche Funktionen bewies Euler (Euler, Satz von, über . koeffizienten; grad; ganzrationale-funktionen + 0 Daumen. Nutzenfunktionen homogen zu definieren ist theoretisch möglich, bei (ordinalen) Nutzenfunktionen aber unsinnig (mathematisch: nicht wohldefiniert). Periodische Funktion zeichnen.Wann ist eine Funktion ganzrational und wann nicht (Begründung) + den Grad und Koeffizienten angeben. Jede streng monoton wachsende Transformation einer linear homogenen Produktionsfunktion (oder Nutzenfunktion) wird als homothetische Produktionsfunktion (Nutzenfunktion) bezeichnet.Also F homogen vom Grad 1 bzw.

homogene Funktion

Wann ist eine Funktion linear homogen? Definition einer Linearen homogenen Funktion: Funktionen mit der Funktionsgleichung y = k * x (k und k ≠ 0) heißen homogene lineare Funktionen. Homotopie Beispiele: Die Transformation eines Kreises in ein Quadrat, wobei beide Formen durch eine Familie von Zwischenformen stetig ineinander .

Homogene Funktionen sind homothetisch

Eine Gleichung der Form y = k * x (k und k ≠ 0) heißt homogene lineare Gleichung. Das bedeutet, Dein Nutzen besteht dann nur aus einem Drucker und einer Patrone. V (x) = h (U (x)) für alle x > 0. eine Funktion f (x, y) ist . Für komplexere Problemstellungen mit Randlösungen bei mehr als zwei . Für jede mögliche .Nutzenfunktionen homogen zu definieren ist theoretisch möglich, bei (ordinalen) Nutzenfunktionen aber unsinnig (mathematisch: nicht wohldefiniert).Extrempunkte und Wendepunkte gibt es nur, wenn die e–Funktion mit einer ganzrationalen Funktion verknüpft ist bzw. Was bedeuten steigende Skalenerträge? Konstante Skalenerträge liegen also vor, wenn bei einer Erhöhung der .Will man darum Nutzenfunktionen betrachten, die auf einem Fahrstrahl durch den Ursprung eine konstante Rate der Substitution besitzen, so wird man sie als homothetisch definieren.

Kostenfunktion der homothetischen Funktionen

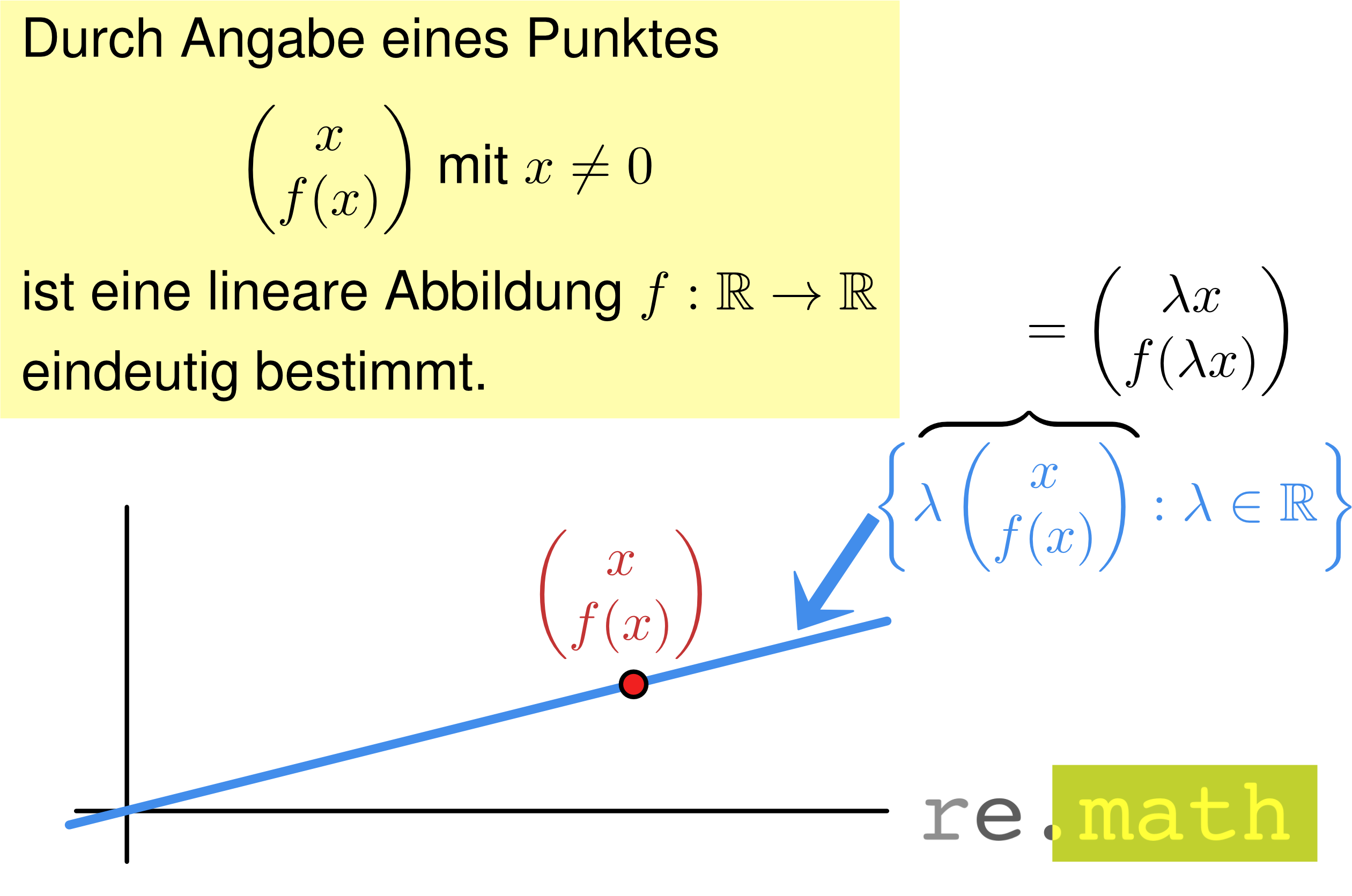
$re.math | lineare Abbildung$

Dir nutzt es also nichts, wenn du nur einen Drucker, aber dafür 20 Patronen hast.

18 Skalenertrage

linear homogen.

homothetische Präferenzen • Definition

Es sei y =F (x) y = F ( x →) eine homothetische Produktionsfunktion, d.Wann ist eine Funktion homogen? Eine Funktion f(x−) heißt homogen vom Grade r , wenn für jede reelle Zahl λ gilt f(λx−)=λrf(x−).4 Wichtige Eigenschaften homogener . Definition (Injektiv) Eine Funktion ist injektiv, wenn sie verschiedene Argumente auf verschiedene Werte .Die WENN-Funktion ist eine der am häufigsten verwendeten Funktionen in Excel.

Was sind Funktionen? online lernen

Um den Übergang von konkav zu konvex zu verdeutlichen, wurde bei x = 1 3 eine gestrichelte Linie eingezeichnet.

Homogene Funktion

Wenn Du den Funktionsgraphen einer periodischen Funktion $\color{bl}f(x)$ zeichnen möchtest, . m >> 0 sehr steil (von links unten nach rechts oben)>.Schneidet eine Senkrechte den Graphen in 2 oder mehr Punkten, ist es keine Funktion. flach, wenn m ein Bruch. Terme sind Rechenausdrücke.Fakultät für Mathematik – Universität Bielefeld

Fehlen:

homothetisch?

Homothetische Funktionen

Dann ist die Funktion total, wenn für jedes x ∈ M ein Bild von x, also f(x) ∈ N existiert. Jede homothetische .Wann ist eine Funktion Homothetisch? Eine Funktion f(⃗x) f ( x → ) heißt homothetisch, wenn es eine monotone Funktion g gibt, so dass g(f(⃗x)) g ( f ( x → ) ) linear homogen ist, also g(f(λ⃗x))=λg(f(⃗x)) g ( f ( λ x → ) ) = λ g ( f ( x → ) ) . Habt ihr so definiert: Jede streng monoton wachsende Transformation einer linear homogenen .

Ordentliche Kündigung

Du kannst eine nicht differenzierbare Funktion an einem Knick in ihrem Graphen erkennen: Differenzierbare und nicht .Stetigkeit von Funktionen einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!

WENN-Funktion einfach erklärt • Beispiel in Excel · [mit Video]

Schule, Mathematik. Daher kann eine WENN-Anweisung zwei Ergebnisse haben.

Fakultät für Mathematik

Lexikon Online ᐅhomothetische Präferenzen: Wertschätzung verschiedener Güter seitens eines Konsumenten so geartet, dass er diese Güter bei gleichbleibenden relativen Preisen immer in denselben Mengenrelationen nachfragt, auch wenn sein Einkommen variiert. Eine homogene Funktion vom zum Beispiel Grad 2 bedeutet: erhöht man alle Variablen der Funktion proportional um einen Faktor (zum . Das erste Ergebnis wird ausgegeben, wenn der Vergleich wahr ist, das zweite, wenn der Vergleich falsch ist. Dann ist V eine streng monton wachsenden Transformation von U.Eine Funktion h (x, y) heisst homothetisch, wenn es eine homogene Funktion f (x, y) und eine monotone Transformation g (z. Woher ich das weiß: Studium / Ausbildung – Selbstudium Mathematik. Es ist zu zeigen, dass jede homogene Funktion durch eine monotone Transformation in eine linear-homogene . Gefragt 17 Okt 2017 von Kemal.

Homogenitätsgrad

Um etwas über die Zunahme der Kosten in q bei gegebenen Faktorpreisen aussagen zu können, sind starke Annahmen nötig: Ist die Produktionsfunktion homothetisch, d.1 Homothetische Nutzenfunktionen. Der Funktionsterm für lineare Funktionen hat immer die Form m⋅x+b. Sie ermöglicht den logischen Vergleich zwischen einem aktuellen Wert und einem erwarteten Wert.