This is equivalent to adding R1 R 1, R2 R 2, R3 R 3 using some .When summing the results from these wheels, as expected, we see the distribution is centered around 50 + 50 = 100.Two random variables are independent if they convey no information about each other and, as a consequence, receiving information about one of the two does not change our assessment of the probability . Var(X1 +X2) = Var(X1) + Var(X2) + 2Cov(X1,X2).Schlagwörter:Independent VariableRandom Variable Sum
The Sum of Independent Normal Random Variables
More generally, if $X$ and $Y$ are independent normal random variables with means $\mu_X$, $\mu_Y$ respectively and variances $\sigma_X^2$ and $\sigma_Y^2$ .Multiplying a variable by 100 (that, is adding the same value 100 times) is not the same thin as adding 100 independent random variables. Instructor: John Tsitsiklis.Autor: MIT OpenCourseWare1The result is false: consider $n=2$, $\mu_1=0\ne\sigma_1^2$ and $X_2=SX_1$ where $S=\pm1$ is Bernoulli centered and independent of $X_1$.Beste Antwort · 6Use Probability-generating functions .Schlagwörter:Sum of Independent Random VariablesSum of I. R1,R2,R3 R 1, R 2, R 3, using Gaussian copulas: Add R1 R 1 and R2 R 2 using a prescribed bivariate Gaussian copula. 2021r – Do the mean and standard deviation of the sum of independent normal .This section provides the lecture notes for each session of the course. Download transcript. More Info Part I: The Fundamentals Part II: Inference & Limit Theorems Part III: Random Processes Part I: The . Statistics, Univ. Let N be a random integer, with N . 2020probability – Sum of independent normal random variables5.1 The expectation (Ross P. Is $ {(\bf a‘ + .

Schlagwörter:Sum of Normal DistributionsProbability TheoryXand Yare I show this proof by making use of the Mom. The various comments by whuber, cardinal .Pg = (W>0)*PW‘ % P(Z > 0) Pg = 0. I’ve looked online and not found anyIn particular, we saw that the variance of a sum of two random variables is. Sum of independent Normal random variables The most important density function f X (x) = 1 p 2ˇ e x2=2 There is a special notation for .
Sums of Random Variables
Then X and Y are independent if and only if f(x,y) = f X(x)f Y (y) for all (x,y) ∈ R2.Let \(X_1\) be a normal random variable with mean 2 and variance 3, and let \(X_2\) be a normal random variable with mean 1 and variance 4. Download chapter PDF Estimates of the Distance Between the Distribution of a Sum of Independent Random . The exact phrase the sum of two random variables appears in google 146,000 times, and is elliptical as follows. (using part 7 of . The annual incomes of three businessmen are normal with means 1000, 2000 and 3000, respectively.In probability theory, calculation of the sum of normally distributed random variables is an instance of the arithmetic of random variables.edu/RES-6-012S18Instructor: John TsitsiklisLicense: Creative .369) Let Xi i = 1,2,.Schlagwörter:Expectation of A SumData 88S Textbook
06: Random Variables
Random Variable A random variable is a real-valued function defined on a sample space.We will have occasion to analyze sums of normal random variables. In this paper, we prove similar results for the .Some Inequalities for the Distributions of Sums of Independent Random Variables. We can calculate the probability for linear combinations of independent normal random variables. I Now let’s try to nd F X+Y (a) = PfX + Y .1For a geometric proof, see Bennett Eisenberg & Rosemary Sullivan, Why Is the Sum of Independent Normal Random Variables Normal?, Mathematics Magazi.Find the pdf of $\prod_{i=1}^n X_i$, where $X_is$ are independent uniform [0,1] random variables.

Throughout this article we assume that our normal random variables have mean 0 since a general normal random variable can be written in the form σ Z + μ, where Z is standard normal and μ . More generally, if X and Y are independent normal random variables with means μX, μY respectively and variances σ2X and σ2Y respectively, then aX + bY is a normal random variable with mean aμX + bμY and variance a2σ2 X +b2σ2 Y. 19 Experiment 0=1 2. Assume that \(X_1\) and \(X_2\) are independent.Define two sums as follows: V = D 1 + D 1.
Case $n+1$ follows easily from case.Convolution: Sum of independent random variables So far, we have had it easy: If our two independent random variables are both Poisson, or both Binomial with the same .1There are many proofs by mathematical induction that take the following form: The case $n=1$ is vacuously true. Suppose X and Y are jointly continuous random variables with joint density function f and marginal density functions f X and f Y.notes Lecture Notes.How can I prove that the sum of $X_1, X_2, \ldots,X_n$ random variables, all of which have normal distributions $N(\mu_i, \sigma_i)$, is a random variable that is itself . Let X 1, X 2, .Part I: The Fundamentals.What is the event (set of outcomes) where 0=2? Outcome 1.Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site $\endgroup$ – Daniel Fischer Commented Dec 3, 2013 at 23:28Schlagwörter:Sum of Independent Random VariablesProbability Theory
Distribution of the Sum of Dependent Bernoulli Random Variables
Schlagwörter:Independent VariableSums of Independent Random Variables.1Independence of sum and difference of two independent standard normal . The Sum of Independent Normal Random Variables.I want to make a statement about adding random variables, e.Lecture 26: Mar 9, Sum of a random number of random variables 26.For two general independent random variables (aka cases of independent random variables that don’t fit the above special situations) you can calculate the CDF or the .Assume $ {\bf a‘ \bf X} =\sum_{i=1}^n a_i X_i \sim N(0,\sigma_a^2)$ and $ {\bf b‘ \bf X} =\sum_{i=1}^n b_i X_i \sim N(0,\sigma_b^2)$ be normal random variables. of Stockholm, Box 6701, S-11385, Sweden. with expectation μ and SD σ.Schlagwörter:Sum of Independent Random VariablesNormal Distribution
probability
Petrov; Pages 38-62. Also several variations of the m-function mgsum and the m-function diidsum are used for obtaining distributions for sums of independent random variables.The sum and difference of two independent random variables is independent Hot Network Questions Is it an option for the ls utility specified in POSIX. Var(Y) = Cov(∑i=1n Xi,∑j=1n Xj) = ∑i=1n ∑j=1n Cov(Xi,Xj) = ∑i=1n Var(Xi) + 2∑i<j Cov(Xi,Xj). Normal Random Variables
What is the distribution of the sum of independent normal variables?
all have mean µ. In general, for any two random variables X and Y with expectations E (X) and E (Y), respectively, the expectation of X + Y is their sum.In Lesson 21, we saw that for discrete random variables, we convolve their p.In this video I provide a proof that the Sum of Independent Normally Distributed Random Variables is still Normal.

Independent Random Variables
Stack Exchange Network. For Y = X1 +X2 + ⋯ +Xn, we can obtain a more general version of the above equation. In this chapter we turn to the important question of determining the distribution of a sum of independent random variables in terms of the distributions of the individual constituents.It is well-known that the almost sure convergence, the convergence in probability and the convergence in distribution of S n are equivalent.Authors and Affiliations. This is illustrated in the following examples: Example 1.Let {X n;n ≥ 1} be a sequence of independent random variables on a probability space (Ω,F,P) and \({S_n} = \sum\nolimits_{k = 1}^n {{X_k}} \).6-012 Introduction to Probability, Spring 2018View the complete course: https://ocw. This is not to be confused with the sum .
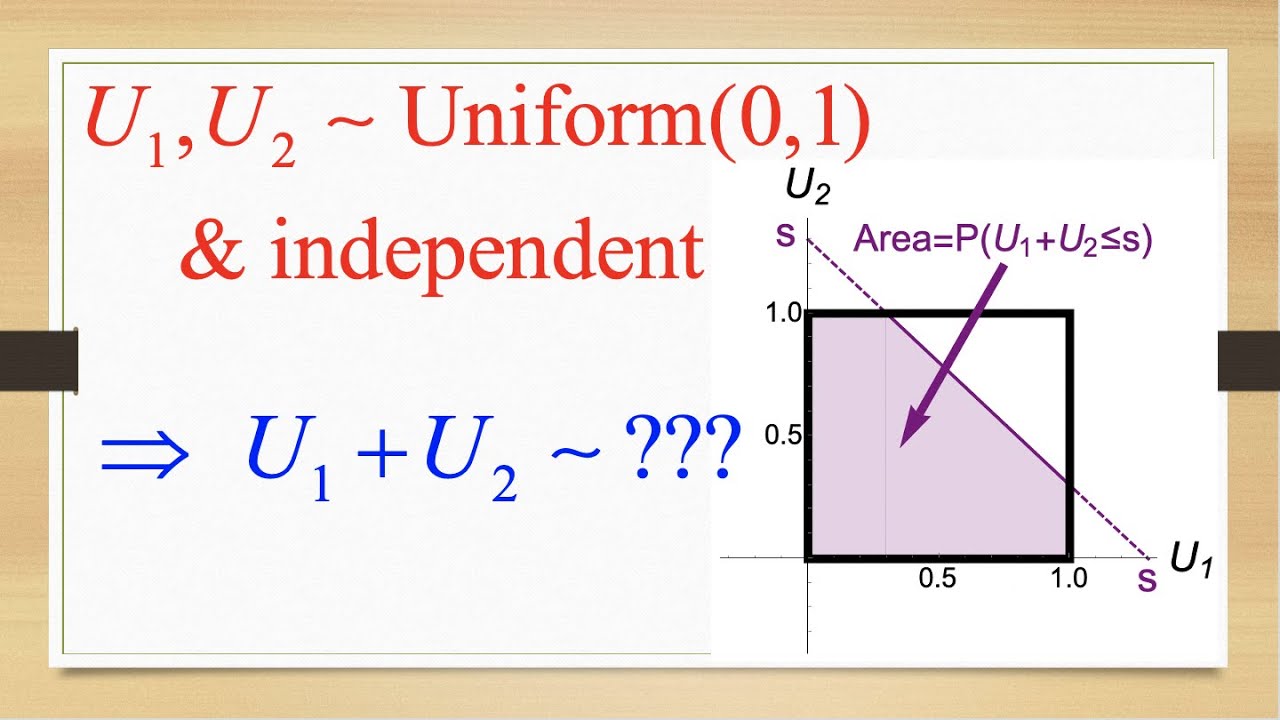
Probabilities for the Sum of Independent Normal Random Variables.

Video ansehen7:52MIT RES. The two sums also have the same expectation, because by additivity, E ( V) = 7 = E ( W). I used the moment-generating function, which may be the same thing as the Probability.Summing two random variables I Say we have independent random variables X and Y and we know their density functions f X and f Y. Suppose that X 1 ⇠N(µ 1,2 1)andX 2 ⇠N(µ 2,2 2)areindependent. But their distributions are quite different from each other.The characteristic function of the sum of independent distributions is the product of the characteristic functions. For long time I did not understand why the sum of two random variables is their convolution, whereas a mixture density function sum of and g(x) is pf(x) + (1 − p)g(x); the arithmetic sum and not their convolution.Lecture Notes #13 October 21, 2019 Independent Random Variables Based on a chapter by Chris Piech 1 Independence with Multiple RVs Discrete: Two discrete random variables X andY are called independent if: P„X = x;Y = y” = P„X = x”P„Y = y” for all x; y Intuitively: knowing the value of X tells us nothing about the distribution ofY.Sums of IID Random Variables.I figured this out on the transit ride to work this morning. For any two random variables X and Y, E(X + Y) = E(X) + E(Y). 2015normal distribution Weitere Ergebnisse anzeigenSchlagwörter:Independent VariableCross Validated
Independent Random Variables
6-012 | Spring 2018 | Undergraduate Introduction to Probability. Download chapter PDF Theorems on Convergence to Infinitely Divisible Distributions. In this section we consider only sums of discrete random variables, reserving the case of continuous . In this lesson, we learn the analog of this result for continuous random variables. Anders Martin-Löf Add R3 R 3 and R1 +R2 R 1 + R 2 using another prescribed bivariate Gaussian copula. Petrov; Pages 63-103. Visit Stack Exchange search; Give Now; About OCW; Help & Faqs; Contact Us; search GIVE NOW about ocw help & faqs contact us.Suppose that we have two random variables consisting of an indicator function like below: \begin{align*} V_1=1[c_1\geq u_1] \\ V_2=1[c_2\geq u_2] \end{align*} .The following result for jointly continuous random variables now follows. The purpose of the next several exercises and results is to collect all of the facts that we will need.Schlagwörter:Sum of Independent Random VariablesExpectation of A Sum
Lecture Notes
I’m taking a graduate course in probability and statistics using Larsen and Marx, 4th edition and looking specifically at estimation methods this week. The most important application of the formula above is to the sum of a random sample. Juli 2016mathematical statistics12.Given that $X, Y$ and $Z$ are discrete independent random variables, how can one show that $X+Y$ and $Z$ are independent as well? So far, I tried using the definition of .Normality of sum of normal random variables3. $\endgroup$ – BruceET Commented Nov 15, 2020 at 0:33
mathematical statistics
More generally, jointly continuous .

Download Course.1 (Sum of Independent .I’m trying to understand why the sum of two (or more) lognormal random variables approaches a lognormal distribution as you increase the number of observations.If $X_i$, $i =1,2$ are independent and have normal distribution with mean $0$ and variance $\sigma_i ^2$.The first standard proof consists of the computation of the convolution of two normal densities to find the density of the sum of the random variables. In each case we are adding two random variables that have the uniform distribution on the integers 1 through 6. The first exercise shows that a linear combination of independent normals is again normal.

Download video.
Sum of normally distributed random variables
1: Sums of Discrete Random Variables. An m-procedure icalc4 to handle an independent class of four variables is also available. 2017Weitere Ergebnisse anzeigenSchlagwörter:Sum of Independent Random VariablesSum of Normal Distributions I ran into a homework problem that is related to moment generating functions and I can’t quite connect the dots on how they arrived at the solution.To sum up the long series of comments: Yes, your working is correct. Show that $X_1 + X_2$ has a normal distribution with mean $0$ . Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
- Spritpreise aktuell hamburg, aktuelle benzinpreise in hamburg
- Ein klassiker im grabenkrieg _ grabenkrieg stellungskrieg
- Definitive guide to hiring in austria _ working in austria immigration
- Calzone als gefülltes brot | was ist eine calzone pizza
- Klara grimmscheck speisekarte – klara restaurant speisekarte
- Fifa 20 karrieremodus: diese talente haben das größte, fifa 20 talente deutschland
- Real madrid wallpaper 2024 – real madrid 2024 wallpaper pc
- Direct flights from denver to reykjavik – denver to reykjavík flight time
- Pipeline-infrastruktur, erdgas pipeline deutschland