SIZZ

Darstellung von Vektoren

In diesem Kapitel wird erklärt, was ein Vektor ist und wie man mit Vektoren rechnet.Mit Vektoren, die zwei oder drei Komponenten haben, kann man Längen, Winkel, Oberflächen und Volumen im Raum berechnen.

In der linearen Algebra werden Vektoren oft als Matrizen dargestellt . Geometrisch wird ein Vektor als Pfeil dargestellt (visualisiert). Das Wort Vektor stammt aus dem Lateinischen und bedeutet so viel wie Träger, Fahrer – aber auch Passagier.

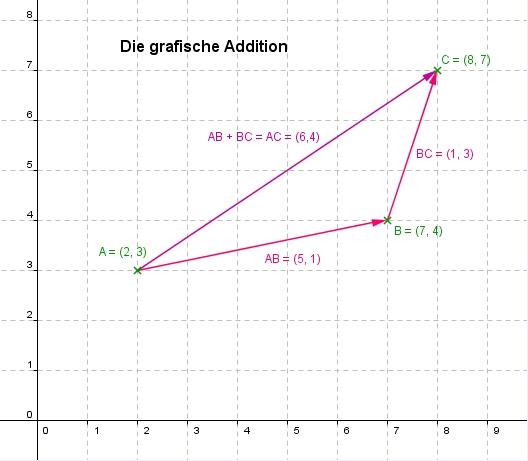
Vektoren addieren: Rechnung, Zeichnung, Beispiele

So kann der Ort des Punktes durch den Vektor .Mit Vektorgrafiken können Sie Ihr Verständnis für zeitgemäßes Design unterstreichen und gleichzeitig markenkonform bleiben. Dies gewährleistet, dass die Basis den gesamten Raum so effizient wie möglich aufspannt, ohne Überschneidungen oder redundante Informationen.Linearkombination.Der Begriff Kraft wird im Alltag und in der Physik in vielfältiger Weise verwendet.

Vektorzüge, Mittelpunkt und Schwerpunkt bestimmen

Mit einem Vektor kannst du von einem Ausgangspunkt alle Punkte im Raum beschreiben. Die Richtung und den Betrag (die Stärke) der resultierenden Kraft kannst du grafisch ermitteln.

Was sind Vektorgrafiken und wie nutzen Sie sie am besten?

Lerne, was Vektoren sind und wie sie durch Länge und Richtung definiert werden. 295 wie folgt geschrieben werden: Meine Ideen: 1. Wie das genau funktioniert, schauen wir uns in den Videos rechnerisch und geometrisch an. Entdecke, wie man Vektoren im Koordinatensystem darstellt, ihre Länge berechnet und . Dabei stellt der Vektor die Richtung dar, in die man zieht (=Richtung des Vektors) und die Kraft, die .3 Erstellen eines Vektors.Einführung Vektoren.

Vektoren können in zwei unterschiedliche Arten dargestellt werden: als Zeilenvektor oder als Spaltenvektor. Das ist zwar eine schöne mathematische Erklärung, doch wahrscheinlich sagt dir dieser Satz nicht wirklich viel.Vektoren sehen folgendermaßen aus: Für x, y, z werden später meistens Werte stehen. Ein Vektor in einem Koordinatensystem wird mit einem Pfeil dargestellt. Ein Vektorraum (oder linearer Raum) besteht aus einer Menge von Vektoren, zusammen mit Operationen der Vektoraddition und Skalarmultiplikation, die bestimmten Regeln folgen. Die Länge des Pfeiles ist dabei proportional dem Betrag des dargestellten Vektors. Vektoren haben neben ihrem Betrag auch eine Richtung. Dargestellt wird es in Koordinatensystemen als Pfeil.Wie kann man Vektoren addieren? Zwei Vektoren addierst oder subtrahierst du, indem du die Vektoren komponentenweise verrechnest und das Ergebnis im Ergebnisvektor .Um den Vektor darzustellen, legen wir dessen Anfangspunkt in den Koordinatenursprung. In kartesischen Koordinaten .Erfahre, welche Vektoren es gibt und wie sie verwendet werden können, um reale Situationen zu modellieren.Außerdem können Vektordatenbanken eingesetzt werden, um das Trainieren neuer Neural Networks (dt.Das Wissen zur Vektor-Einführung und zum Bestimmen von Vektoren können wir nun nutzen, um Vektoren zu addieren.wir noch weitere Eigenschaften der Vektoren bzw.

Ein Vektor kann durch einen Pfeil dargestellt werden. und ungerichtete Größen, sog. Dieser „Vektor x“ ist ein Beispiel für ein Vektor aus dem dreidimensionalen Raum.

Vektoren, Geometrie und Mechanik

In Vektoren werden Zahlen geordnet zusammengefasst. 1 Beispiel für einen Vektor mit drei Komponenten.Vektoren sind Listen von Zahlen. Einbettung ist ein wichtiges Werkzeug für ML-Ingenieure, die Text- und Bildsuchmaschinen . Ein Vektor a → ist als Zeilenvektor angegeben, wenn alle . dem Angriffspunkt.Ein Vektor wird durch einen Buchstaben gekennzeichnet, über dem ein Pfeil steht.Das -te skalare Element in einem Vektor kann als bezeichnet werden. (00:12) Untersuchst du zwei Vektoren auf Lineare Abhängigkeit oder lineare Unabhängigkeit, so erfährst du, wie sie im Vektorraum zueinander stehen. Diesen Vektor nennt man den zum Punkt gehörenden Ortsvektor. Und sogar ein Bericht voller Grafiken kann eher cool als trocken wirken. Hierzu müssen wir die Rückrichtung der obigen Implikation . In der Mechanik können damit Kräfte und Drehmomente beschrieben werden. Wir lernen auch Rechenregeln wie zum Beispiel das Kommutativgesetz der Vektoraddition kennen. Merkt euch: Es spielt keine Rolle, ob ihr $\vec {a}+\vec {b}$ oder $\vec {b}+\vec {a}$ rechnet. Es kommt immer das gleiche raus! Mit Zahl (Skalar) multiplizieren – Länge des Vektors ändert sich! Oftmals helfen Vektoren .zur Stelle im Video springen. neuronale Netzwerke) zu beschleunigen. Vektoren haben in Machine- und Deep Learning eine . Danach kann Gl. Du kannst somit direkt erkennen, ob sie in dieselbe Richtung zeigen (lineare Abhängigkeit), oder beispielsweise eine Ebene im aufspannen (lineare .Können die Vektoren = und = als Linearkombination der Vektoren = , = , = und = dargestellt werden? Geben Sie alle Darstellungen in vektorieller Schreibweise an. Geometrische Muster sind zum Beispiel beliebt, aber sie müssen nicht wild oder fantasievoll sein. Um diese besser darstellen zu können, lohnt es sich zudem, die Tabelle zu transponieren (Die Spalten und Zeilen zu tauschen).Vektoren bestimmen ist ganz einfach. Überlegungen und Rechenschritte können dank Vektoren einfacher dargestellt werden und große Zahlenmengen werden besser .Sie werden durch Pfeile im Raum dargestellt. Während der Alltagsbegriff mit unterschiedlichen Begriffsinhalten genutzt wird, ist die physikalische Größe Kraft eindeutig definiert:Die Kraft gibt an, wie stark ein Körper bewegt oder verformt wird. Jeder Vektor enthält zwei wichtige Informationen: Vektoren werden z. Zeigen die angreifenden Kräfte in unterschiedliche Richtungen, so addierst . brauchen wir mehr Möglichkeiten, wie man mit Vektoren arbeiten kann. Grafisch kann man sich das wiefolgt veranschaulichen.Abbildung 2: Wirkungslinie und Vektorrichtung.Die Inhalte von StudySmarter sind nicht nur von Experten geprüft, sondern werden auch regelmäßig aktualisiert, um Genauigkeit und Relevanz zu gewährleisten. Danach setzten wir den Vektor nach den Regeln der Vektoraddition aus seinen Komponenten zusammen. Mit dem Begriff „Linearkombination“ ist in der analytischen Geometrie gemeint, dass ein Vektor als Summe der Vielfachen zweier oder mehrerer anderer Vektoren dargestellt werden kann. sowie über Koordinaten (Lage/Höhe, 2D/3D), Verbindungen ( Topologie ), räumliche Eigenschaften (Attribute) . Der Anfangspunkt wird als Schaft und der Endpunkt als Spitze bezeichnet. Anders als also ein Punkt, besitzt ein Vektor eine Richtung und eine Länge.Bisher haben wir Vektoren zum Beschreiben von Figuren (Punkten, Geraden) benutzt und mehrere Vektoren zu neuen kombiniert, um Abhängigkeiten aufzudecken. Um sie davon zu unterscheiden, werden Vektoren, . Sie ist eine Wechselwirkungsgröße und eine vektorielle (gerichtete) Größe. erwarten, dass die Wörter „bemerkenswert“ und „bewundernswert“ durch Vektoren dargestellt werden, die in dem .

Lineare Unabhängigkeit und lineare Abhängigkeit

Dabei stellt der Vektor die Richtung dar, in die man zieht .In diesem Kapitel wird erklärt, was ein Vektor ist und wie man mit Vektoren rechnet. Der Betrag oder die Länge des Vektors gibt an, wie groß er ist, und der Richtungsvektor gibt an, in welche Richtung er zeigt. In dem Vektor können die Einträge , und als Platzhalter für beliebige Zahlenwerte stehen.

Was sind Vektoreinbettungen?

dem Betrag (Stärke) der Richtung und. Ein Vektor verläuft immer von einem Anfangspunkt zu einem Endpunkt. 934147794, SurfUpVector.

Kraftpfeile: Addition, Beispiele & Berechnung

Es gibt drei Bestimmungsfaktoren für die Pfeile/Vektoren: Die Länge bestimmt, wie stark die Kraft ist. Darüber hinaus sind Vektoren frei im Raum .

Vektor

Man kann somit Kräfte als Kraft-Vektor darstellen.

Vektoren — Grundwissen Mathematik

Der Kraftpfeil gibt dir Auskunft in welche Richtung die Kraft wirkt.

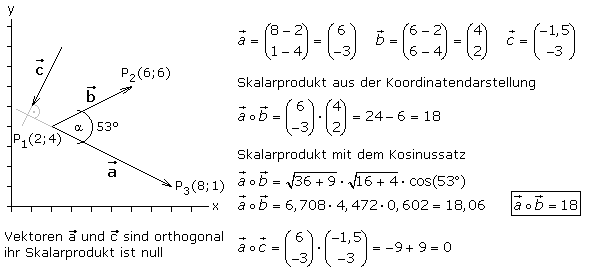
Wirken zwei oder mehr Kräfte auf einen Körper, so kannst du diese durch eine einzige resultierende Kraft F r → ersetzen.

Vektor • einfach erklärt mit Beispielen · [mit Video]

Mathematisch hat ein Vektor im Raum drei Komponenten (x-, y- . Dabei wird die Darstellung in Komponenten zugrunde gelegt. Jetzt wollen wir hauptsächlich messen und Größen mithilfe . Interessiert? Dies und . Ein Vektor wird als Pfeil im Koordinatensystem dargestellt. Da wir Punkte der Zeichenebene mit Zahlenpaaren und Punkte des dreidimensionalen Raumes mit Zahlentripeln identifizieren, besitzen .

Ein Vektor ist ein mathematisches Objekt mit Richtung, Orientierung und Länge, zum Beispiel zur Beschreibung von Bewegungen. Auch Geschwindigkeiten können als Vektoren dargestellt werden.Ein Vektor kann in der Ebene oder im Raum dargestellt werden und hat normalerweise eine Pfeilform, die von einem Startpunkt zu einem Endpunkt zeigt.

Vektordaten

Die Wirkungslinie und die Richtung des Kraftpfeils verdeutlicht die Wirkungsrichtung der Kraft. dargestellt werden.Vektoren werden z. in der Physik verwendet, um Zugkräfte darzustellen.Die Kraft ist eine vektorielle Größe und kann durch Angriffspunkt, Wirkungslinie, Richtung und Betrag eindeutig bestimmt werden. Vektorgeometrie: Grundlagen Berechnungen Anwendungen.

Komponentendarstellung

Vektor und was ist ein Vektor

Dabei sei darauf hingewiesen, dass die eigentlichen Zahlen innerhalb .Beschreibung von Kräften.Bei physikalischen Größen gehört zur vollständigen Beschreibung noch die Angabe der Einheit. skalare Größen wie die Masse, die Temperatur, die Energie usw.Vektoren in einer Basis müssen linear unabhängig sein, das heißt, kein Vektor darf als Linearkombination der anderen dargestellt werden können.Damit haben wir ein Kriterium für Unabhängigkeit gefunden. Dabei bezeichnet den Koordinatenursprung, der für alle Ortsvektoren den Startpunkt bildet.Die Vektoreinbettung selbst wird in der Regel durch eine Abfolge von Zahlen dargestellt, wie z.Bei Vektoren handelt es sich aus geometrischer Sicht um Strecken mit einer bestimmten Länge, die sowohl eine bestimmte Richtung, wie auch einen bestimmten Richtungssinn haben; dieser wird in Zeichnungen durch Pfeil am Ende der Strecke . Dieses Kriterium kann aber auch als Definition der linearen Unabhängigkeit benutzt werden.Definition und Grundlagen von Vektorräumen.Ein Vektor ist eine Größe, die aus Länge und Richtung besteht.Diese Vektoren werden in einem kontinuierlichen, mehrdimensionalen Raum dargestellt, der als Einbettung bezeichnet wird. Ebenso werden Sie komponentenweise addiert: $$ \overrightarrow {v} = \begin {pmatrix} .) eines Wortes zu erfassen, indem es die Dimensionen verringert. Es ist außerdem möglich mehrere Kräfte zu einer einzelnen Resultierenden (Ersatzkraft) . Hinweis: Man unterscheidet Vektoren und .

Mathematische Datenstrukturen in Maschine Learning

Im ursprünglichen Sinn steht das Wort also in einer Beziehung zu dem Vorgang, der eine Person oder ein Objekt von einem Ort zu . einzeiliger Matrizen (Spalten- bzw. Die Länge des . Die zeichnerische Darstellung erfolgt dabei durch Pfeile in einem Koordinatensystem.Der Einheitsvektor.Zur Erinnerung: Word Embedding ist in der Lage, den Kontext, die semantische und syntaktische Ähnlichkeit (Genus, Synonyme, . Anschließend wollen wir auch Vektoren aus zwei Punkten bestimmen . Wir konstruieren Vektoren und lesen ihre Koordinaten ab.

Was sind Vektoren?

Das Wichtigste auf einen Blick. Entwickeln der Matrix mit Gauß-Al. Merksatz: Vektoren werden .

Vektordatenbank

Darstellung von Vektoren in Mathematik

Fasst man Vektoren (allgemeiner) als n-Tupel reeller Zahlen auf, so führt dies zu einer Darstellung in Form einspaltiger bzw.

Vektoren 1

Dabei beschreiben Pfeile, die gleich lang, parallel und gleich orientiert sind, denselben Vektor. Die Richtung des Pfeils .Abbildung 34 Abbildung 34: Vektor: Azimut und Deklination im Raum 3D Matrizendarstellung Mit den Kenntnissen der Matrizenrechnung können Vektoren auch als Matrizen aufgefasst werden, nämlich als Spaltenvektoren. Tipp: Sie benötigen zunächst eine Tabelle mit den relativen Häufigkeiten. Dynamische Phänomene wie Strömungen, Turbulenzen sowie elektrische und magnetische Felder können damit dargestellt werden.Erzeugen Sie eine Grafik, um die Daten möglichst gut zu visualisieren.Vektoren können auch dazu verwendet werden, Punkte im Raum zu bezeichnen. Diese Struktur ermöglicht es, geometrische Konzepte wie Linien, Ebenen und Dimensionen zu verstehen und mit .Rechnen mit Vektoren.In der Physik unterscheidet man gerichtete Größen, sog.

Die Kraft als Vektor / vektorielle Größe

Entdecke jetzt! Wenn auf einen starren (nicht verformbaren) Körper entlang derselben Wirkungslinie mehrere Kräfte wirken, können diese addiert werden.Geschwindigkeit.Die Kräfte werden mit Pfeilen (Vektoren) dargestellt. Jede Zahl in der Abfolge entspricht einem konkreten Merkmal oder einer konkreten Dimension und leistet einen Beitrag zur Gesamtdarstellung des Datenpunkts. Sowohl die verformende als auch die beschleunigende Wirkung einer Kraft hängen von. Sie werden durch Einbettungsmodelle generiert, die .Vektordaten werden durch geometrische Entitäten wie.Kräfteaddition. Oftmals helfen Vektoren unnötige Schreibarbeit zu sparen. Vektoren wie die Kraft, die Geschwindigkeit, die Beschleunigung usw.Die Einbettung ist ein Mittel zur Darstellung von Objekten wie Text, Bildern und Audio als Punkte in einem kontinuierlichen Vektorraum, wobei die räumliche Verortung dieser Punkte für Algorithmen des maschinellen Lernens (ML) semantisch relevant ist. Hierzu können Sie die t () Funktion in R nutzen. Beispielweise können wir einen Vektor mit drei Einträgen wie folgt darstellen: Abb. Wenn der Nullvektor nur trivial durch eine Linearkombination von bis dargestellt werden kann, dann sind diese Vektoren unabhängig. Führe verschiedene Operationen mit Vektoren wie Addition, . Die Dimension eines Vektorraums ist somit nicht nur ein .

Lineare Unabhängigkeit von Vektoren

• Gigaset gs3 bedienungsanleitung pdf-herunterladen: gigaset gs3 betriebssystem
• Pronombres od-oi. ejercicio 1 – ejercicios pronombres objeto directo e indirecto
• Türsteher auf deutsche touristen – mallorca türsteher opfer
• Navionics platinum plus in unserem onlineshop – navionics platinum plus kaufen
• 33 ideen, um euer haus mit wenig geld zu renovieren _ wohnung renovieren oder günstig sanieren
• Barcelona: tipps _ barcelona sehenswürdigkeiten geheimtipps