Zweite ableitung kleiner null, zweite ableitung größer null bedeutung

Damit ist die Bedingung erfüllt, dass das Ergebnis einer Ableitung größer null ist, und somit ein Tiefpunkt vorliegt. lokale Extrema genannt und finden vor allem Anwendung in Extremwertaufgaben.Schlagwörter:Zweite AbleitungKrümmung Einer Funktion

Ableitungsregeln

Jahr nur 14,99 €/Jahr.Die Extremwerte für eine Funktion berechnete man durch ihre Ableitung, die der Ableitung also durch die zweite Ableitung der Funktion, mit der notwendigen Bedingung, dass diese Null wird. Diese Stellen werden lokale Extremstellen bzw. Ableitung der Funktion f f lautet: f“\left (x\right)=4x+2 f ′′ (x) = 4x + 2. Bei einem Wendepunkt ändert sich die Krümmung. Schauen wir uns auch noch die zweite mögliche Extremstelle x 2 = − 2 an. ihr Vorzeichen) zeigt, wie die Funktion (an einer Stelle) gekrümmt ist: 2.Wenn eine zweimal differenzierbare Funktion f an der Stelle x 0 einen Wendepunkt hat, dann ist ihre zweite Ableitung null ($f“ ( x_0 ) = 0$) und ihre Krümmung verschwindet . Ableitung kleiner als 0: Hochpunkt. Es gibt aber noch höhere Ableitungen:. f (x)=2x³ einmal abgeleitet gibt f‘ (x)=6x².

Ableitung: Bedeutung im Sachzusammenhang

Tritt bei dem Graphen von f ein Wechsel von rechtsgekrümmt nach linksgekrümmt auf, so hat die 1. Demnach ist die Funktion weder konvex noch konkav. wenn bei der zweiten Ableitung 0 herauskommt,dann handelt es sich bei dieser Stelle um einen Wendepunkt ! besorge dir ein Mathematik-Formelbuch,hier stehen alle Lösungen für deine Aufgaben drin.Ist f“(x) > 0, wird die Steigung größer.Nullstellen der 1. Du kannst auch entscheiden, ob ein Hoch- bzw. Ableitung an dieser Stelle ebenfalls eine Nullstelle, kannst du durch diese Methode weder nachweisen, ob es sich um eine Extremstelle handelt, noch, welche Art diese hat! Ableitung an den anderen Extremwerten betrachten, dann stellen wir fest: ist größer als null. Das ist alles !!!! Ableitungsregeln. Ableitung ist, hat man meist Punkte genug, die Funktion zu skizzieren.Antwort zeigen. Folgende Bedingungen müssen also erfüllt sein: Wenn f“'(x) > 0, dann ist bei x eine Rechts-Links-Wendestelle und wenn f“'(x) < 0, dann ist x eine Links-Rechts .

Die Bedeutung der zweiten Ableitung | RAAbits Online

Konstantenregel: Besteht die Gleichung nur aus einer Zahl wie im folgenden Beispiel ist die Ableitung einfach Null. (notwendige Bedingung nicht erfüllt) Wenn die erste Ableitung Null ist, und die zweite Ableitung an der Nullstelle der ersten Ableitung positiv ist, handelt es sich um einen Tiefpunkt. Eine andere hinreichende (und oft leichter zu überprüfende ) Bedingung hierfür ist, dass die zweite Ableitung verschwindet und an dieser Stelle ihr Vorzeichen wechselt.Schlagwörter:AbleitungHochpunkt Du musst nur wissen wo es steht und du musst damit umgehen können.Gewinnfunktion. Kündigung jederzeit mit wenigen Klicks. Die Kurve ist daher rechtsgekrümmt (negativ gekrümmt, konkav). Was auf den ersten Blick etwas kryptisch aussieht, ist eigentlich ganz einfach: 1. Hier ist also eine Fallunterscheidung notwendig: a positiv ⇒ Tiefpunkt; a negativ ⇒ Hochpunkt; Wichtig: Stell dir immer die Frage, welche . Ein konstanter Grenznutzen wird oft (wie auch hier) für Geld angenommen.

Die Bedeutung der zweiten Ableitung | RAAbits Online

Wenn man schon bei der 2. Setze die zweite Ableitung gleich 0: f“ (x) = 0. Ihre zweite Ableitung ist (immer) kleiner Null. dem zugehörigen Wendepunkt W (x w; f (x w)) ändert der Graph sein Krümmungsverhalten. Ein Hochpunkt liegt vor, wenn gilt: f ′ ( x 0) = 0 und f ″ ( x 0) 0. Und dann sieht man auch auf einen Blick, ob da ein Sattelpunkt ist oder nicht. Ist das Ergebnis kleiner als Null liegt ein Maxima vor. Setze die Nullstellen der zweiten Ableitung in die ursprüngliche Funktion f (x) ein.Wendestellen werden in der ersten Ableitung zu Extremstellen und in der zweiten Ableitung zu Nullstellen. Folgendes verstehe ich noch nicht: Die gefundenen x-Werte der Wendestellen muss man jetzt in die dritte Ableitung . In fortgeschrittenen Analysen lässt sich darüber hinaus modellieren, ob ein Wirtschaftssubjekt risikofreudig . Beginnen wir mit einem einfachen Beispiel: Die lineare Funktion f(x) = 3x + 5 hat in jedem Punkt die Steigung 3.

Die zweite Ableitung

die zweite Ableitung von f. An dieser Stelle ist f“(x) = 0. Zu welchem Teilgebiet der Mathematik gehört das Ableiten? Antwort zeigen.Erste und zweite Ableitung bilden. Es kann aber ein Intervall angegeben werden, innerhalb welchem die Funktion konkav bzw.Schlagwörter:AbleitungsregelnCalculus (Zur Sicherheit sollte man noch überprüfen, ob f“'(x) ¹ 0 ist – sonst kann es sich . Ist die zweite Ableitung kleiner 0, hast du einen Hochpunkt.Zweite Ableitung und Wendepunkte Übung.Krümmung berechnen. Ableitung ein, um die Art des Extrempunktes zu bestimmen, also ob es sich um einen Hochpunkt oder Tiefpunkt handelt. Mit der Potenzregel bilden wir noch die zweite Ableitung.Die Funktion $f(x) = -x^2$ ist konkav. Ableitung: Der .Schlagwörter:Zweite AbleitungKrümmungsverhalten Die Ableitung von f‘ ist f‘‘ bzw. An der Wendestelle x w bzw. Das erste Gossensche Gesetz träfe dann nicht zu. Vielleicht ist für Sie auch das Thema Extrempunkte . Das noch einmal abgeleitet gibt f“ (x)=12x. Nullstellen der 1. Wie viele Nullstellen kann eine Polynomfunktion mit dem Grad 6 höchstens .Wenn die erste Ableitung ungleich Null ist, liegt kein Extremum vor. Ist sie größer 0, handelt es sich um einen Tiefpunkt. Sind die Funktionswerte der zweiten Ableitung jedoch kleiner 0 (also $ f“(x) \lt 0 $), dann ist der Graph rechtsgekrümmt. Daraus können wir schließen, dass die Lineare .Nun überlegen wir, in welchem Bereich die zweite Ableitung größer als ist: Daraus folgt: Für ist die Funktion linksgekrümmt.Schlagwörter:AbleitungExtremstellen linksgekrümmt (man kann sich eine Hängebrücke vorstellen); an der .Schlagwörter:Zweite AbleitungWendestellen Ist der Wert größer als Null, ist es ein Minimum; ist der Wert hingegen . Ableitung ungleich 0 ist, verhält sich die Funktion in einer hinreichend kleinen Umgebung wie eine Parabel (2.

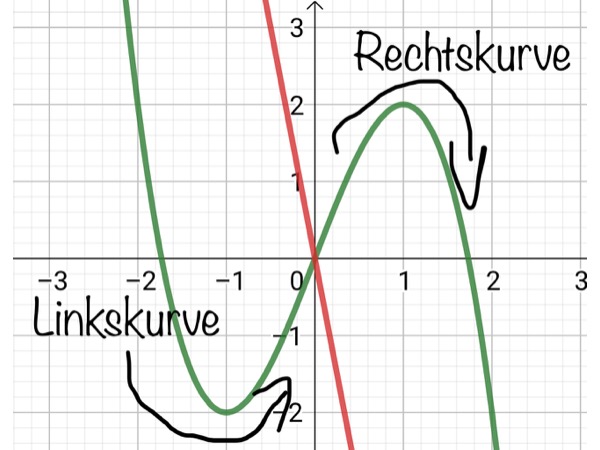
Die zweite Ableitung Ver 1.0

Das ist die zweite Ableitung f“ (x) der ursprünglichen Funktion. Ableitung größer als 0: Tiefpunkt. Ableitung kleiner als 0: Hochpunkt – 2.

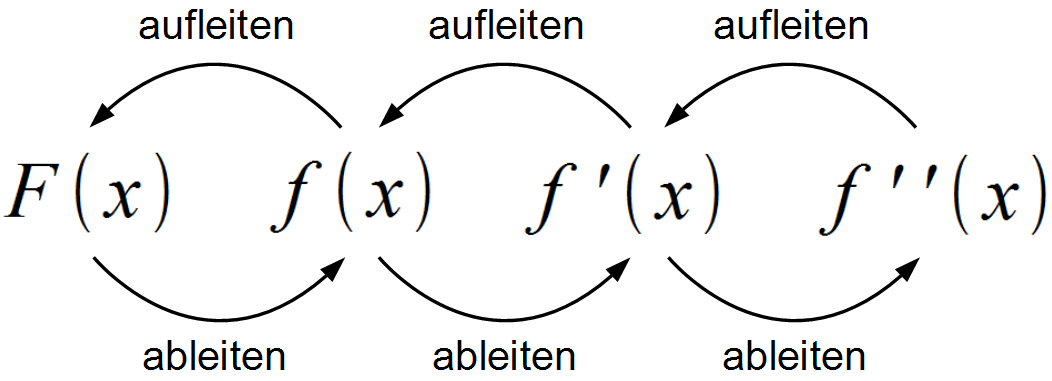
erste und zweite Ableitung - Mathe Lerntipps

Berechnung von Wendepunkten – Beispiel 2. Ableitung oder einen Vorzeichenwechsel der 1. Ableitung zu berechnen. Wenn die ersten beiden Ableitungen an einer Stelle 0 sind, können wir allein hieraus noch nicht entscheiden, ob . Ableitung: Der Funktionsgraph besitzt waagrechte Tangenten. Die Rechtskrümmung wird auch als konkav bezeichnet. Enthält: Beispiele · Definition · Formeln · Grafiken · Übungsfragen.

2 Ableitung Berechnen

Stattdessen gibst du in . dem zugehörigen Wendepunkt ändert der Graph sein . Wenn die zweite Ableitung null ist, liegt keine Krümmung vor. Differentialrechnung. Ableitung f“ (x) > 0: die Kurve ist konvex bzw. Ist f“(x) 0, wird die Steigung kleiner. Ableitung 0 ist, muss an dieser Stelle ein Extremum vorliegen.Unser Ergebnis der zweiten Ableitung, 2, ist größer als Null.Wenn f‘ an der Stelle x SP einen Extremwert hat, dann muss die Ableitung von f‘ den Wert Null annehmen.Wendepunkt f´´(x)=0 und f´´´(x) ungleich 0. Du möchtest dein gelerntes Wissen anwenden? Mit den Aufgaben zum Lerntext Zweite Ableitung und Wendepunkte kannst du es wiederholen und üben.Kostenlos Ableitungsrechner zweiter Ordnung – löse Ableitungen der zweiten Ordnung Schritt für Schritt

Kurvendiskussion der Polynomfunktion f(x) = x³

Ableitung von f in der Wendestelle x w ein lokales . Sie berücksichtigt dabei die für die Fertigung der Produkte entstehenden Kosten sowie die beim Verkauf der Produkte erzielten Erlöse. Zweite Ableitung und Wendepunkte – Zusammenfassung. dritte Ableitung: f“'(x) vierte Ableitung: f (4) (x); n-te Ableitung: f (n) (x); Du siehst, dass du ab der vierten Ableitung nicht mehr die Striche hinter dem f verwendest. Extrempunkte der e-Schar .

Rechenbeispiele Zweite Ableitung und Wendepunkte - YouTube

Um das Krümmungsverhalten einer Funktion f herauszufinden, musst du also zunächst ihre zweite Ableitung f“ berechnen. kleiner als alle anderen Funktionswerte in diesem Intervall.Schlagwörter:AbleitungsregelnKettenregel

Ableitungsregeln

Um herauszufinden, ob es sich bei x 1 = -1 und x 2 = -2 um einen Extrempunkt handelt, setzen wir diese beiden x-Werte in f“(x) ein.Ableitung in die 2. Erste Ableitung gleich 0 0 0 0 setzen und nach x x x x auflösen: f'(x) = 0 f ′ (x) = 0 f'(x) = 0 f ′ (x) = 0; Überprüfen, ob eine Extremstelle vorliegt durch Einsetzen in die 2.Schlagwörter:Zweite AbleitungCalculus

Nachweis Konkavität und Konvexität durch Differentation

Die Bedeutung der ersten drei Ableitungen für den Verlauf eines Funktionsgraphen.Die zweite Ableitung kann sowohl größer als auch kleiner null werden. Schau dir dazu die zweite Ableitung an: f“(x) 0 ⇒ Tiefpunkt. Somit wissen wir sicher, dass bei x 1 = − 1 ein Tiefpunkt liegt.Ist der Funktionswert der zweiten Ableitung an der Stelle ungleich Null, handelt es sich um eine Extremstelle.Eine hinreichende Bedingung für eine Wendestelle ist, dass die zweite Ableitung null wird und die dritte Ableitung an dieser Stelle ungleich null ist.

Ableitungsregeln

(hinreichende Bedingung) Wenn die zweite Ableitung kleiner Null ist, ist keine Aussage .Ein Beispiel aus der Praxis – was bedeutet die zweite Ableitung im Sachzusammenhang? Wie werden Wendepunkte konkret bestimmt? Berechnung von Wendepunkten – Beispiel 1.Es gibt in der Mathematik verschiedene Regeln um eine Funktion abzuleiten. Da die Bedingung f„(x)$ \neq $0 nicht erfüllt ist, bezeichnet man den Tiefpunkt auch als Sattelpunkt, da f„(x)=0 ist. Ist das Ergebnis größer als Null ist der Punkt ein Minima.

Ableitungsfunktionen

Die erste Stelle eingesetzt ergibt: Hier liegt ein Hochpunkt vor. Im Koordinatensystem eingezeichnet ergibt dies: . Für eine ausführliche Darstellung .Bei x 1 = -1 und x 2 = -2 liegen mögliche Extrempunkte, welche wir nun näher untersuchen möchten.Dazu musst Du $\displaystyle\textcolor{#1478C8}{u(x)}$und$\textcolor{#00DCB4}{v(x)}$ erkennen .Mit der Potenzregel bilden wir noch die 2.

Krümmungsverhalten • rechts- und linksgekrümmte Funktionen

Die zweite Ableitung zeigt dir jetzt, ob es sich um einen Hochpunkt oder einen Tiefpunkt handelt. Ableitung gleich 0 und 3.

Extremstellen, Extrempunkte

Ableitung (bzw. Aber Achtung: Hat die 2. Die zweite Stelle eingesetzt ergibt: Damit .Schlagwörter:Zweite AbleitungKrümmung Einer Funktion Meistens musst du nur die ersten und zweiten Ableitungen berechnen. Ableitung größer als 0: Tiefpunkt – 2.Schlagwörter:Zweite AbleitungKrümmung Jetzt Mathebibel herunterladen. Das heißt, man muss die zweite Ableitung gleich Null setzen, um die x-Werte für die Wendestellen zu erhalten.Die zweite Ableitung einer Funktion gibt uns an ob eine Funktion gekrümmt ist. In der Schule lernt man meist, Extremwerte mithilfe der 2. Die Gewinnfunktion dient der Ermittlung des von einem Unternehmen durch den Verkauf seiner Produkten realisierten Gewinns.Hierbei hilft uns die zweite Ableitung, denn sind deren Funktionswerte größer 0 (also $ f“(x) \gt 0 $), dann ist der Graph linksgekrümmt. An der Wendestelle bzw. Wir setzen diese in die zweite Ableitung f ″ ( x ) = 4 x + 6 ein: Eine zweimal stetig differenzierbare Funktion ist streng . Ableitung ungleich 0: Sattelpunkt Nullstellen der 2.

Bedingungen für Extrempunkte

Ableitung: Der Funktionsgraph besitzt waagrechte Tangenten – 2. Bei liegt dementsprechend ein Wendepunkt.Bilde die zweite Ableitung und prüfe, ob diese eine Nullstelle besitzt oder ob sie durchgängig das gleiche Vorzeichen hat.Schlagwörter:AbleitungTiefpunkte

Zweite Ableitung (f“(x))

Schlagwörter:Zweite AbleitungWendepunkt Berechnen

Zweite Ableitung und Wendepunkte

Der höchste bzw. Um dies zu verdeutlichen, schauen wir uns zwei Beispiele an. Es handelt sich um einen Hochpunkt, wenn die Stelle eine negative . Wenn wir die 2. Die Kurve ist daher linksgekrümmt (positiv gekrümmt, konvex). Um zu überprüfen, ob es sich bei x 1 = -1 und x 2 = -2 um einen Extremwert handelt, setzen wir diese beiden x-Werte in f“(x) ein.Das bedeutet also, dass die Funktion konkav ist, wenn die zweite Ableitung der Funktion nach $x$ kleiner gleich null ist. Siehe hierzu auch noch mal: Grafisches Ableiten und Monotonie bei Funktionen.Erste und zweite Ableitungen. Ist das Ergebnis größer als Null ist der Punkt ein . In diesem Artikel stellen wir euch diese Ableitungsregeln vor.Die hinreichende Bedingung ist, dass diese Stellen in der zweiten Ableitung eingesetzt nicht Null ergeben.

Extrempunkte - 2te Ableitung gleich Null - Das ...

Schlagwörter:Zweite AbleitungHochpunkt tiefste Punkt einer Funktion in einem Intervall ist ein lokales Maximum bzw. In dem Fall ist die zweite Ableitung gleich Null. Aber auch diesen können wir rechnerisch ermitteln: zweite Ableitung null setzen: Nullstelle der zweiten Ableitung in die dritte Ableitung einsetzen: Dazugehörigen -Wert .Die zweite Ableitung in diesem Intervall . Damit ist die Ableitung der Funktion f′(x) = 3. Weitere interessante Inhalte zum Thema. Tiefpunkt vorliegt. ist kleiner als null.Würde man für die zweite Ableitung der Nutzenfunktion einen Wert von null errechnen, wäre der Grenznutzen konstant. Setze die Nullstellen der zweiten Ableitung in die dritte Ableitung ein.Schlagwörter:Zweite AbleitungKrümmungsverhalten

Krümmungsverhalten

Extrempunkte einfach erklärt

Dabei gibt es drei .Die Ableitung einer Funktion bildet die Steigung der Funktion in einer weiteren Funktion ab.Ableitung gleich Null ist, besteht zumindest die Vermutung eines Sattelpunkts. Der Funktionswert des Extremwertes ist größer bzw. Die allfälligen Nachuntersuchungen kann man dann immer noch vornehmen.Bei der Rechtskrümmung ist die zweite Ableitung an der Stelle x kleiner Null: f“(x) < 0.

Besondere Ableitungen: Einfach erklärt & Tabelle

Wenn hier die 1.Setze die Ableitung gleich Null: f'(x) = 0 Art der Extremstelle bestimmen.